Й способ вывода уравнения Эйлера, основанный на принципе Даламбера

В качестве примера рассмотрим РК центробежного компрессора (рис. 3.20).

Выделим на некотором радиусе R элементарную частицу газа δm, которая перемещается в относительном движении в межлопаточном канале по траектории с радиусом кривизны R_W.

Определимсилы инерции, действующие на выделенную элементарную частицу газа.

Поскольку частица перемещается при вращении РК с угловой скоростью ω по некоторому радиусу R, следовательно, на нее действует центробежная сила в переносном движении .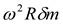

В относительном движении частица также перемещается по дуге окружности, следовательно, на нее будет действовать центробежная сила в относительном движении .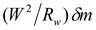

Как известно, в случае участия одновременно в двух движениях – относительном и переносном, к частице приложена кориолисова сила 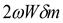. Направление ее совпадает с направлением вектора 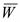, повернутого на 90º в сторону, противоположную вращению колеса.

Кроме того, в случае наличия вязкости, будет иметь место касательная сила трения в относительном движении .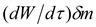

В соответствии с принципом Даламбера векторная сумма сил инерции равна и противоположна по направлению сумме действующих сил, то есть для определения затрат работы можно воспользоваться только силами инерции.

Таким образом, чтобы определить внешний момент M_z, приложенный к колесу, можно просуммировать моменты, вызванные силами инерции:

.

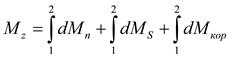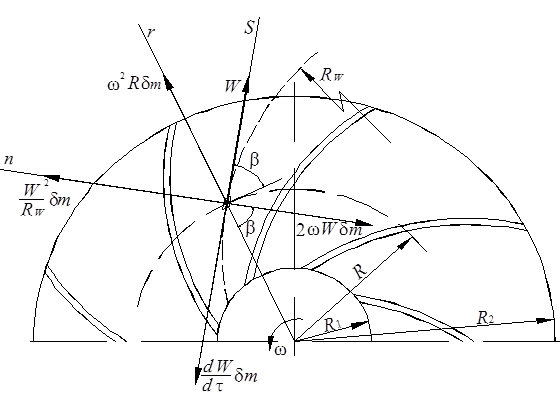
Рис. 3.20. К выводу уравнения Эйлера по 1-му способу: R_w – радиус кривизны траектории частицы в относительном движении; R₂–радиус наружной поверхности РК; R₁ – радиус входа на лопатки

Примем момент положительным (dM>0), если он направлен против направления угловой скорости ω.

Поэтому моменты сил инерции, действующие относительно оси вращения z, будут иметь следующие знаки:

• по оси r - dM_r= 0;

• по оси n - dM_n< 0; dM_кор> 0;

• по оси s - dM_s< 0.

Момент от центробежной силы в относительном движении

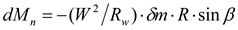. (3.20)

Момент от касательной силы трения

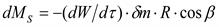. (3.21)

Момент от кориолисовой силы

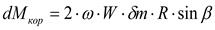. (3.22)

Преобразуем уравнения (3.20)– (3.22) с учетом того, что:

• относительная скорость есть производная пути по времени ;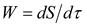

• отношение массы элементарной частицы к бесконечно малому интервалу времени есть массовый расход ;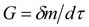

• радиус кривизны траектории частицы в относительном движении описывается уравнением ;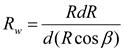

• синус текущего угла установки лопатки на некотором радиусе R

.

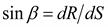С учетом этих соотношений преобразуем выражения (3.20) – (3.22).

Момент от центробежной силы в относительном движении

,

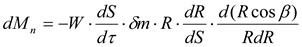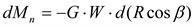. (3.23)

Момент от касательной силы трения

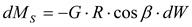(3.24)

Момент от кориолисовой силы

,

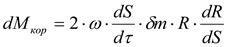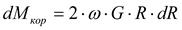. (3.25)

Теоретический напор ,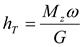

.

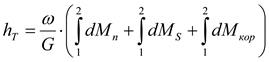Подставив в последнее выражение формулы (3.23) – (3.25), получим

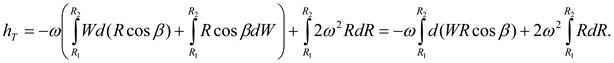
Интегрируя по радиусу от R₁до R₂

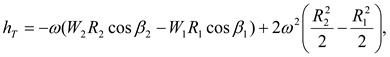
с учетом того, что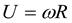

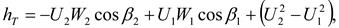
из треугольника скоростей (рис. 3.21) известно: 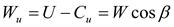, поэтому

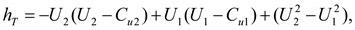
раскрывая скобки, получаем

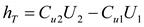. (3.26)

Выражение (3.26) называется уравнением Эйлера в форме записи через закрутки потока.

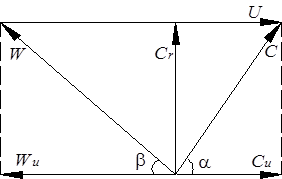Рис. 3.20. Треугольник скоростей: 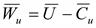;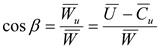