Математические модели местности
Математической моделью местности (МММ) называют математическую интерпретацию цифровых моделей для компьютерного решения конкретных инженерных задач. В зависимости от инженерного назначения математической модели для одной и той же Ц М М может быть использовано несколько различных МММ.
ЦММ и М М М используют прежде всего для получения необходимой исходной информации для автоматизированного проектирования (продольные профили земли по оси трассы, поперечные профили, инженерно-геологические разрезы и т.д.). Возможности цифрового и математического моделирования позволяют в корне изменить технологию проектирования инженерных объектов и требуют изменения технологии и методов сбора, регистрации и представления исходных данных при изысканиях.
Цифровые и математические модели, представляемые в геодезических прямоугольных координатах, тем не менее могут характеризоваться различной точностью и степенью детализации элементов рельефа, ситуации, что связано с категорией рельефа, ситуационными особенностями аппроксимируемого участка местности, масштабами используемых для построения Ц М М топографических планов и материалов аэросъемок, принятым типом цифровой модели, плотностью исходных точек и методикой аппроксимации поверхности. Математические связи между исходными точками цифровых моделей описываются линейными либо нелинейными (степенными) зависимостями. В первом случае связь между смежными точками модели описывается уравнениями плоскостей, проходящими через каждые три смежные точки модели.Во втором — криволинейными поверхностями разного порядка, и, таким образом, рельеф местности задается либо множеством пересекающихся между собой плоскостей, либо поверхностей различной кривизны. Решение наиболее актуальной задачи при математическом моделировании рельефа местности заключается в определении высот точек местности.Подавляющее число регулярных и нерегулярных ЦММ предполагают при последующем математическом моделировании линейную интерполяцию высот между смежными точками модели.
Линейное моделирование рельефа:
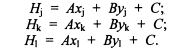
Если в уравнения подставить известные координаты трех исходных точек цифровой модели, то получим три уравнения, в которых не известны только три коэффициента А, В и С
22.Пространственная триангуляция Делоне
Задача построение сети неперекрывающихся треугольников является одной из базовых в вычислительной геометрии и широко используется в машинной графике и геоинформационных системах для моделирования поверхности и решения пространственных задач.
Впервые задача построения сети неперекрывающихся треугольников была поставлена в 1934 году в работе советского математика Б. Н. Делоне, который сформулировал и соответствующие условия.
В математике задачей построения триангуляции по заданным точкам называют задачу их попарного соединения непересекающимися отрезками так, чтобы образовалась сеть треугольников.
Основными элементами триангуляции Делоне являются:
узлы (вершины треугольников), ребра (стороны) и грани (собственно треугольники).
Построенная триангуляция может быть:
• выпуклой (если таковым будет минимальный многоугольник, охватывающий область моделирования),
• невыпуклой (если триангуляция не является выпуклой) и оптимальной (если сумма длин всех ребер минимальна).
| Рис. Элементы триангуляции Делоне |
| a |
| b |
| Грань |
| Узел |
| Ребро |
Сеть таких треугольников называется триангуляцией Делоне, если она удовлетворяет некоторым условиям:
• внутрь окружности, описанной вокруг любого треугольника, не попадает ни одна из исходных точек;
• триангуляция является выпуклой и удовлетворяет сформулированному выше условию Делоне;
• сумма минимальных углов всех треугольников максимальна из всех возможных триангуляций;
• сумма радиусов окружностей, описанных около треугольников, минимальна среди всех возможных триангуляций.
Первый из названных выше критериев (внутрь окружности, описанной вокруг любого треугольника, не попадает ни одна из исходных точек) построения триангуляции Делоне, называемый круговым, является одним из основных и проверяется для любой пары треугольников с общими гранями. Математическая интерпретация критерия вытекает из рисунка.
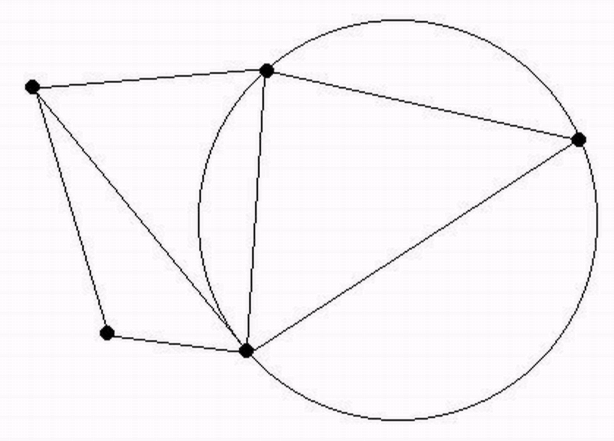
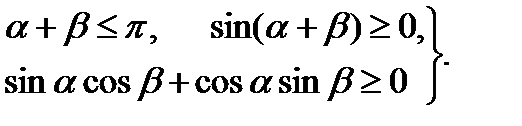
О точности пространственной триангуляции Делоне.
Располагая пикеты на характерных элементах рельефа (например, водоразделах и тальвегах), мы игнорируем более мелкие элементы в промежутках. При построении горизонталей1 по таким ребрам треугольников возникает ошибка, которая зависит от величины неровности рельефа и угла наклона местности. Например, средняя погрешность съемки рельефа, не должна превышать 1/3 сечения рельефа при углах наклона поверхности от 2 до 10 градусов. Можно рассчитать, что при сечении рельефа 0,5 м предельная величина пропущенной неровности (то есть отклонения поверхности земли от прямой, проходящей через соседние пикеты) не должна превышать (0,5/3)*cos10°=0,16 м.
Триангуляция Делоне.
В настоящее время существует множество алгоритмов построения триангуляции Делоне. Многие из известных алгоритмов используют определение триангуляции Делоне как вторичный признак триангуляции. Поэтому в таких алгоритмах отмечаются следующие слабости:
– алгоритмы используют постоянно вычисляемые тригонометрические функции, что резко замедляет процесс;
– при исследовании взаимоотношения точек и базового отрезка возникают очень малые углы, и при использовании тригонометрических функций постоянно появляется опасность исчезновения порядка и деления на «0» в связи с ограниченной точностью представлений данных в компьютере.
Наиболее известные программные продукты строят триангуляцию Делоне, используя теорему о пустом шаре как основной, первичный принцип построения треугольников. Алгоритм выглядит так:
– все множество точек делится на треугольники, т.е. создаются комбинации из трех точек;
– для каждой комбинации находится описанная окружность и координаты ее центра;
– если внутри окружности текущей комбинации не находится ни одной точки из оставшихся то эта комбинация есть треугольник – часть триангуляции Делоне.
К достоинствам этого алгоритма можно отнести:
– отсутствие использования тригонометрических функций, что не замедляет процесс построений;
– непосредственное построение триангуляции Делоне, без каких – либо предварительных построений;
– простота всех вычислений и преобразований;
– в итоге триангуляционная сетка представлена множеством треугольников, а не отдельных линий.
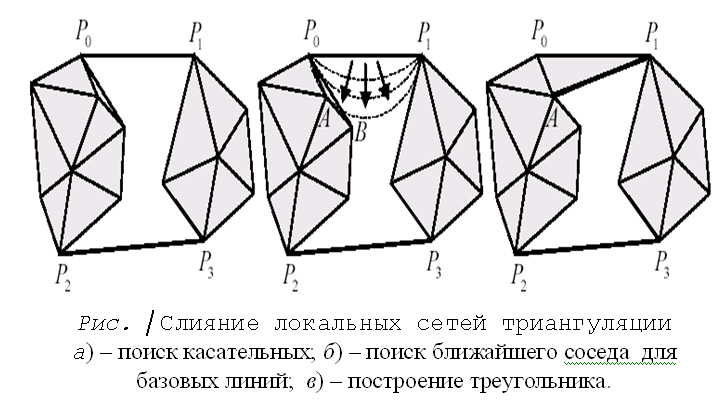
узлы, ребра, грани и структурные линии, а слева – структурныЗадача построения модели поверхности с учетом структурных линий называется триангуляцией Делоне с ограничениями. Фрагмент триангуляции Делоне с включенными в нее дополнительными элементами приведен на рисунке, где справа показаны линии местности (береговые линии, бровки оврага и др.) и точки с известными отметками.
| Рисунок. Структурные линии в модели TIN |
| Озеро |
| Овраг |
| Дорога |
| Река |
Располагая пикеты на характерных элементах рельефа (например, водоразделах и тальвегах), мы игнорируем более мелкие элементы в промежутках. При построении горизонталей1 по таким ребрам треугольников возникает ошибка, которая зависит от величины неровности рельефа и угла наклона местности. Например, средняя погрешность съемки рельефа, не должна превышать 1/3 сечения рельефа при углах наклона поверхности от 2 до 10 градусов. Можно рассчитать, что при сечении рельефа 0,5 м предельная величина пропущенной неровности (то есть отклонения поверхности земли от прямой, проходящей через соседние пикеты) не должна превышать (0,5/3)*cos10°=0,16 м.
Для точности определения объема перемещаемого грунта важна также площадь, занимаемая не учитываемой деталью рельефа. Допустим, в квадрате 20х20 м между двумя парами пикетов имеется цилиндрическая выпуклость с максимальной высотой 0,15 м. Нетрудно подсчитать, что ее неучет при представлении данной поверхности только двумя треугольниками приведет к ошибке приблизительно в 40 м3. Не так уж много, но для участка в 1 га, расположенного на холме или верхней (как правило, выпуклой) части склона, получится уже 40*25=1000 м3 лишнего грунта. Если же брать пикеты в два раза чаще (то есть через 10 м), ошибка уменьшится вчетверо и составит 250 м3 на гектар. Этот фактор можно учесть заранее, поскольку положительные формы равнинного рельефа обычно имеют выпуклую форму, а отрицательные – вогнутую. Если на подлежащий съемке участок имеются приближенные данные о рельефе, то радиус кривизны поверхности и необходимую густоту пикетов легко рассчитать по величинам заложения горизонталей или отдельным высотным отметкам.
