Классификация переменных используемых при эконометрическом моделировании.

В любой эконометрической модели в зависимости от конечных при­кладных целей ее использования все участвующие в ней переменные подразделяются на:

· экзогенные, т. е. задаваемые как бы «извне», автономно, в опреде­ленной степени управляемые (планируемые);

· эндогенные, т.е. такие переменные, значения которых формиру­ются в процессе и внутри функционирования анализируемой социально-экономической системы в существенной мере под воздействием экзогенных переменных и, конечно, во взаимодействии друг с другом; в эконометри­ческой модели они являются предметом объяснения;

· предопределенные, т. е. выступающие в системе в ролифакторов-аргументов,или объясняющих переменных.

Из данных выше определений следует, что множество предопределен­ных переменных формируется из всех экзогенных переменных (которые могут быть «привязаны» к прошлым, текущему или будущим моментам времени) и так называемых лаговых эндогенных переменных, т. е. таких эндогенных переменных, значения которых входят в уравнения анализиру­емой эконометрической системы измеренными в прошлые (по отношению к текущему) моменты времени, а, следовательно, являются уже извест­ными, заданными.

Можно сказать, что эконометрическая модель слу­жит для объяснения поведения эндогенных переменных в зависимости от значения экзогенных и лаговых эндогенных переменных.

5. Метод наименьших квадратов для построения модели.

Метод наименьших квадратов используется для построения математической модели (регрессионной). Основное положение метода наименьших квадратов формулируется следующим образом. Найти зависимость между функциональным признакомУи множеством факторных признаков х1,х2,х3 таким образом, чтобы сумма квадратов отклонений наблюдаемых значений функционального признака в опыте i от значений этого признака, полученных по регрессионной модели, была минимальной: ∑ (Уi - Yр)²→min, где Yi - значение функционального признака в опыте номер i, Yр значение этого признака, рассчитанного по модели.

6. Линейный коэффициент корреляции. Коэффициент детерминации.

Линейный корреляционный анализ позволяет установить прямые связи между переменными величинами по их абсолютным значениям. Формула расчета коэффициента корреляции построена таким образом, что если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона.

В общем виде формула для подсчета коэффициента корреляции такова:

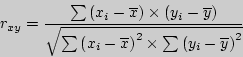
где 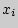- значения, принимаемые переменной X,

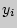- значения, принимаемые переменой Y,

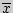- средняя по X,

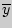- средняя по Y.

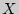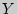Расчет коэффициента корреляции Пирсона предполагает, что переменные и распределены нормально.

Даная формула предполагает, что из каждого значения 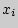переменной X, должно вычитаться ее среднее значение 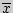. Это не удобно, поэтому для расчета коэффициента корреляции используют не данную формулу, а ее аналог, получаемый с помощью преобразований:

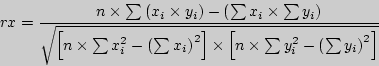
Коэффициент детерминации рассматривают, как правило, в качестве основного показателя, отражающего меру качества регрессионной модели, описывающей связь между зависимой и независимыми переменными модели. Коэффициент детерминации показывает, какая доля вариации объясняемой переменной y учтена в модели и обусловлена влиянием на нее факторов, включенных в модель:

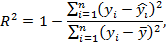
где 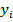– значения наблюдаемой переменной, 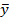– среднее значение по наблюдаемым данным, 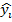– модельные значения, построенные по оцененным параметрам.

7. Оценка существенности параметров линейной корреляции.

Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции m_r:

.

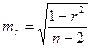Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывается 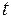-критерий Стьюдента. Выдвигается гипотеза Н₀о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции проводится путем сопоставления их значений с величиной случайной ошибки:

; ; .

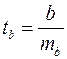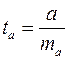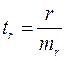Сравниваем фактические и критические (табличные) значения 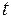-статистики. Еслиt_факт>t_крит, то Н₀ отклоняется, т.е. a, b и r_xy не случайно отличаются от нуля и все они статистически значимы. Иначе, гипотеза Н₀ о случайной природе показателей принимается.

8. Оценка существенности параметров линейной регрессии.

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Оценка значимости уравнения регрессии в целом производится на основе 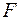-критерия Фишера, который заключается в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_крит значений 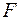-критерия Фишера.F_факт определяется по следующей формуле:

.

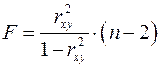где 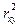- коэффициент детерминации;

n – число единиц совокупности.

F_крит – это максимально возможное значение критерия при данных степенях свободы и уровне значимости α. Уровень значимости α – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01.

Если фактическое значение 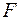-критерия больше табличного, то гипотеза Н₀ отклоняется, т.е. признается статистическая значимость и надежность уравнения регрессии.

В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его случайная ошибка: 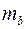и .

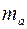Случайные ошибки коэффициентов регрессии определяются по формулам:

.

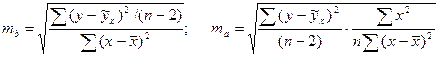9. Интервалы прогноза по линейному уравнению регрессии.

Прогнозирование по уравнению регрессии представляет собой подстановку в уравнение регрессии соответственного значения х. Такой прогноз 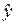называется точечным.

Он не является точным, поэтому дополняется расчетом стандартной ошибки 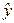. Стандартная ошибка предсказываемого среднего значения зависимой переменной при заданном значении :

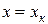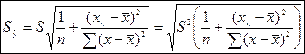
Где 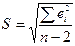- стандартная ошибка регрессии, 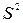- остаточная дисперсия.

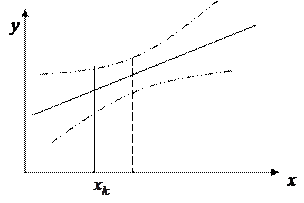Величина 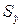достигает минимума при 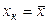и возрастает по мере удаления 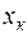от 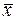в любом направлении.

Получаем интервальную оценку прогнозного значения :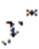

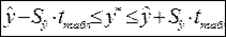
10. Средняя ошибка аппроксимации.

11. Классификация нелинейной регрессии.

Различают два класса нелинейных регрессий:

• регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым па­раметрам;

• регрессии, нелинейные по оцениваемым параметрам.

Примером нелинейной регрессии по включаемым в нее объ­ясняющим переменным

могут служить следующие функции:

• полиномы разных степеней

• равносторонняя гипербола

К нелинейным регрессиям по оцениваемым параметрам от­носятся функции:

• степенная

• показательная

• экспоненциальна

12. Корреляция для нелинейной регрессии.

Уравнение нелинейной регрессии дополняется показателем корреляции – индексом корреляции.

Для любых моделей, в том числе и нелинейных, показатель корреляции вычисляется так:

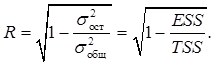
Если модель нелинейная относительно объясняющей переменной приводится к виду парной или множественной регрессии, то линейный коэффициент корреляции совпадает с индексом корреляции.

13. Отбор факторов при построении множественной регрессии.

При построении системы факторов необходимо соблюдать следующие условия: 1) должны быть количественно измеримы; 2) теоретически обоснованы; 3) линейно независимы друг от друга; 4) одна модель не должна включать в себя совокупный фактор и факторы его образующие; 5) тесно связаны между собой. Для реализации 5-го требования строят матрицу коэф-в парной корреляции. На основании этой матрицы выбирают те факторы, связь которых с величиной наиболее тесная. Затем проверяют наличие мультиколлинеарности (МК) факторов. Два фактора МК, если 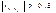. МК факторы нельзя включать в одну модель, нужно выбрать один из них или заменить оба совокупной функцией.

14. Оценка параметров уравнения множественной регрессии.

МНК

Множественная регрессия позволяет построить и проверить модель линейной связи между зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x1,...,xр), где у - зависимая переменная (результативный признак); х1,...,хр - независимые переменные (факторы).

Линейное уравнение множественной корреляции: y=a+b1x1+b2x2+…+bpxp+ε. Для оценки параметров уравнения множественной регрессии применяют МНК. Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:

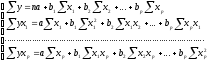
Для ее решения может быть применён метод определителей: a=∆a / ∆, b1=∆b1 / ∆,…, bp=∆bp / ∆, - определитель системы

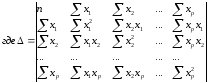
∆a, ∆b1,…, ∆bp – частные определители; которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.

15. Частные коэффициенты корреляции.

Часто возникает необходимость исследовать частную корреляцию между переменными при исключении - элиминировании - влияния остальных переменных. Выборочный частный коэффициент корреляции между переменными Х_i и X_j при фиксированных остальных р-2 переменных определяется выражением:

ri-j,1,2,...,p = ,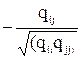

(4.9)

где q_ii и q_jj - алгебраические дополнения элементов r_ii и r_jj матрицы коэффициентов корреляции (для частного случая р=3):

.

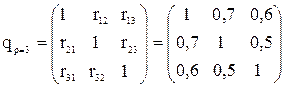(4.10)

16. Парные коэффициенты корреляции.

Коэффициент парной корреляции (Пирсона) — это некоторое число от -1 до 1, характеризующее тесноту линейной корреляционной связи (корреляцию) между зависимой случайной величиной и независимой случайной величиной.

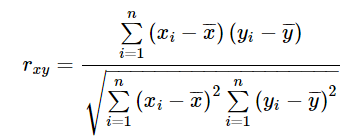
n — число наблюдений;

x_i — i-ое наблюдаемое значение независимой случайной величины;

y_i — i-ое наблюдаемое значение зависимой случайной величины;

r_xy — коэффициент парной корреляции.

17. Проверка значимости коэффициентов корреляции.

Изучение линейной статистической зависимости между переменными Х и Y имеет смысл лишь тогда, когда величина r = 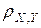значима (или существенна), т. е. не очень близка к нулю. Однако эта величина может быть лишь оценена с помощью выборочных данных.

Точечной оценкой теоретического коэффициента корреляции 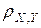является выборочный коэффициент корреляции r = r_xy , который находится по формуле

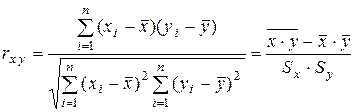. (2.33)

В формуле (2.33)

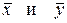– выборочные средние переменных X и Y соответственно;

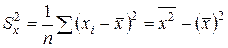– выборочная дисперсия переменной X;

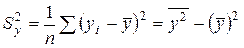– выборочная дисперсия переменной Y;

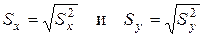– выборочные среднеквадратические (стандартные) отклонения переменных X и Y соответственно;

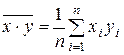– выборочное среднее переменной X× Y .

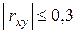– линейная связь отсутствует;

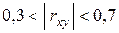– имеется слабая линейная связь;

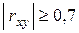– имеется сильная линейная связь. 3

18. Множественный коэффициент корреляции.

Теснота линейной взаимосвязи одной переменной 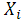с совокупностью других (p 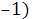переменных 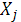рассматриваемой в целом, измеряется с помощью множественного (или совокупного) коэффициента корреляции 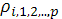, который является обобщением парного коэффициента корреляции 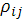Выборочный множественный, или совокупный, коэффициент корреляции 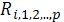, являющийся оценкой 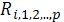, может быть вычислен по формуле:

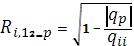(1.40)

Где 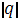определитель матрицы 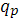; 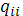алгебраическое дополнение элемента 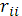той же матрицы.

Множественный коэффициент корреляции заключен в пределах 0 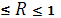. Он не меньше, чем абсолютная величина любого парного или частного коэффициента корреляции с таким же первичным индексом.

С помощью множественного коэффициента корреляции (по мере приближения R к 1) делается вывод о тесноте взаимосвязи, но не о ее направлении. Величина 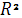, называемая выборочным множественным (или совокупным) коэффициентом детерминации, показывает, какую долю вариации исследуемой переменной объясняет вариация остальных переменных.

19. Значимость коэффициента корреляции.

Даже для независимых величин коэффициент корреляции может оказаться отличным от нуля вследствие случайного рассеяния результатов измерений или вследствие небольшой выборки случайных величин. Поэтому следует проверять значимость коэффициента корреляции.

Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента:

.

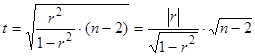Если t > t_кр (P, n-2), то линейный коэффициент корреляции значим, а следовательно, значима и статистическая связь X и Y.

Можно рассчитать значение критического коэффициента корреляции

.

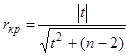Для удобства вычислений созданы таблицы значений доверительных границ коэффициентов корреляции для различного числа степеней свободы f = n–2 (двусторонний критерий) и различных уровней значимости a = 0,1; 0,05; 0,01 и 0,001. Считается, что корреляция значима, если рассчитанный коэффициент корреляции превосходит значение доверительной границы коэффициента корреляции для заданных f и a .

Для больших n и a = 0,01 значение доверительной границы коэффициента корреляции можно вычислить по приближенной формуле

.

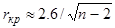20. Суть гетероскедастичности.

Гетероскедастичность (англ. heteroscedasticity) — понятие, используемое в прикладной статистике (чаще всего — в эконометрике), означающее неоднородность наблюдений, выражающуюся в неодинаковой (непостоянной) дисперсии случайной ошибки регрессионной (эконометрической) модели. Гетероскедастичность противоположна гомоскедастичности, означающей однородность наблюдений, то есть постоянство дисперсии случайных ошибок модели.

Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с помощью метода наименьших квадратов. Кроме того, в этом случае оказывается смещённой и несостоятельной классическая оценка ковариационной матрицы МНК-оценок параметров. Следовательно статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим тестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей.

21. Последствия гетероскедастичности.

1. Оценки параметров не будут эффективными, то есть не будут иметь наименьшую дисперсию по сравнению с другими оценками; при этом они будут оставаться несмещенными.

2. Дисперсии оценок будут смещены, так как будет смещена дисперсия на одну степень свободы 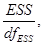которая используется при вычислении оценок дисперсий всех коэффициентов.

3. Выводы, получаемые на основе завышенных F- и t-статистик, и интервальные оценки будут ненадёжны.

22. Обнаружение гетероскедастичности.

Тесты 2х типов: те, что основаны на априорных предпосылках о природе гетероскедастичности, и те, что опираются на них. Для двух категорий, примером могут быть тест Голдфелда-Квандта (применяется если ошибки регрессии можно считать нормально распределенными случайными величинами) и тест Уайта (прослеживает количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров).