Математическое представление метода
С точки зрения математики процедура оценки полезности в рамках совместного анализа выглядит следующим образом.
Модель объекта, в данном случае YouTube канала, задана в виде набора характеристик и их значений. Они и их значения нумеруются как – число характеристик и {1,2, … k} – множество характеристик;
Nj – количество значений характеристик с номером j, j=1,..k; {1,2,… Nj} – ряд значений характеристики с номером j, j=1,..k. Величину
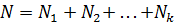
называют длинной общего ряда значений характеристик.
Подобный способ нумерации позволяет записывать профиль объекта как набор значений (l1, l2,…,lk), где lj ∈ {1,2,…, Nj}, j=1,…,k.
Это дает возможность сформировать список объектов, которые различаются значениями характеристик. Этот список включает в себя все возможные варианты, называется полным набором профилей. Если к модели добавить новую характеристику, число вариантов объекта возрастет во столько раз, сколько значений может принимать эта характеристика. Если модель объекта содержит k характеристик, а характеристика j может принимать Nj различных значений j = 1,…k, то полный набор профилей включает K профилей, где
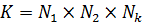
Если профилей много, то респондентам трудно оценивать полезность каждого предложенного им варианта, и вместо полного набора, используют сокращенный набор профилей, иначе называемый ортогональным планом объема K* < K.
Набор профилей, в любом удобном виде, предлагается респондентам для оценивания, структура данных «на входе» модели совместного анализа, т.е оценки полезности профилей полученных от респондентов показаны в таблице 1.
Таблица 1. Структура результатов опроса (оценки полезности профилей).
| Респондент | Варианты объекта | ||||
| … | K* | ||||
| U11 | U12 | U13 | … | U1K* | |
| U21 | U22 | U23 | … | U2K* | |
| … | … | … | … | … | |
| n | Un1 | Un1 | Un1 | … | UnK* |
Где n – количество опрошенных, K* - ортогональный(сокращенный) план профилей, Uil – полезность конкретного объекта с номером l для респондента i. Величину полезности Uil определяет респондент.
Затем, на основе этих оценок, производится оценка полезности рядов значений характеристик – частных полезностей. Декомпозиция полезности объекта на полезность значений характеристик производится отдельно, как для каждого респондента, так и для всей совокупности опрошенных. Для этого используется модель вида:
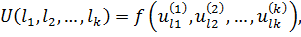
где U(l1,l2,…,lk) – полезность товара, со значением характеристик l1,l2,..,lk, lj∈{1,2,…,Nj}, j = 1,…,k;
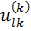 – полезность значения lk атрибута с номером k, k = 1,…,k; (?)
– полезность значения lk атрибута с номером k, k = 1,…,k; (?)
f – функциональная зависимость, между полезностью товара и полезностью значений характеристики.
Рассматривается простая аддитивная модель:
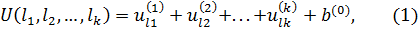
где b(0) – константа.
Результат оценивания модели (1) состоит в том, что для респондента с номером i, i = 1,…n, определяются ряды полезности значений каждого из атрибутов и константу:
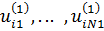 полезности значений 1, … , N1 атрибута 1;
полезности значений 1, … , N1 атрибута 1;
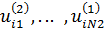 полезности значений 1, … , N2 атрибута 2;
полезности значений 1, … , N2 атрибута 2;
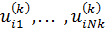 полезности значений 1, … , Nk атрибута k;
полезности значений 1, … , Nk атрибута k;
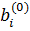 – константа.
– константа.
Для совокупности респондентов в целом, определяют аналогичные величины, без индекса i.
Для оценки величин полезности характеристик объекта, по величинам полезности объекта, с точки зрения респондента с номером i, i = 1,…n; строится еще одна система описания вариантов объекта. Для каждой характеристики j для которой предполагается дискретная функция полезности, вводятся Nj -1 переменных 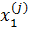 ,
, 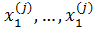 x1(j), x2(j), …, xNj-1(j), которым для каждого профиля приписывают значения по следующим правилам:
x1(j), x2(j), …, xNj-1(j), которым для каждого профиля приписывают значения по следующим правилам:
1. Если атрибут j принимает значение lj и в ряду возможных значений указанного атрибута значение lj не является последним, значение новой переменной с верхним индексом j и нижним индексом lj полагают равным единице, а значения всех остальных новых переменных с верхним индексом j полагают равными нулю: 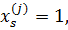 если s = lj,
если s = lj, 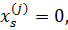 если s ≠ lj; s = 1, … ,Nj – 1;
если s ≠ lj; s = 1, … ,Nj – 1;
2. Если атрибут j принимает последнее возможное значение в ряду, т. е, значение lj=Nj, все новые переменные с верхним индексом j принимают значение (-1): 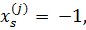 s = 1, … , Nj – 1
s = 1, … , Nj – 1
Для каждой характеристики с линейной функцией полезности, в новой системе описания вводится одна переменная, значения которой совпадают со значением характеристики из описываемого профиля, так же в эту систему описания объекта вводится константа x(0) = 1.
Для i-го респондента строится и оценивается регрессионная модель вида:
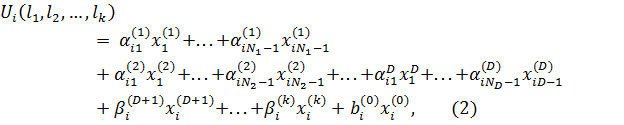
Уравнения строятся для всех вариантов объекта (D – число характеристик с дискретной моделью полезности). Параметры модели (величины 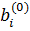 ,
, 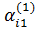 ,…,
,…, 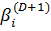 ,
, 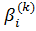 ) оцениваются на основе метода наименьших квадратов, с применением либо специализированного программного обеспечения, либо иных программ с возможностями статистических вычислений. Полезность значений характеристики j с дискретной функцией полезности для i-го респондента, находят по правилу:
) оцениваются на основе метода наименьших квадратов, с применением либо специализированного программного обеспечения, либо иных программ с возможностями статистических вычислений. Полезность значений характеристики j с дискретной функцией полезности для i-го респондента, находят по правилу:
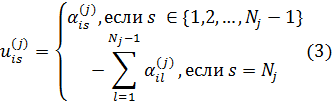
(здесь s = 1, … ,Nj; j = 1, …, D; i = 1, …, n). Полезность значений атрибута j с линейной функцией полезности, для респондента с номером i находят по правилу:
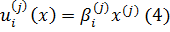
(здесь j = D + 1, …, k; i = 1,…n, а x – значение характеристики).
Структура данных «на выходе» модели совместного анализа показана в таблице 2.
Таблица 2. Структура оцененной модели полезности.
| Респондент | Атрибут 1 | Атрибут 2 | … | Атрибут k | Константа | |||
| N1 | N2 | … | Nk | |||||
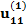 | 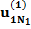 | 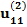 | 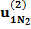 | … | 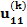 | 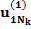 | 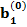 | |
| … | … | … | … | … | … | … | … | … |
| n | 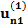 | 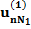 | 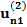 | 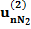 | … | 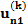 | 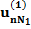 | 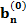 |
| Все | 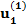 | 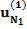 | 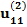 | 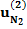 | … | 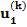 | 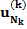 | 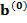 |
Здесь n – количество респондентов, k – количество характеристик, Nj – количество значений характеристики с номером j. В i-ой строке указаны величины:
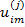 – полезность значения s атрибута j для респондента i, i = 1, …, n; s = 1, …, Nj; j = 1, …, k;
– полезность значения s атрибута j для респондента i, i = 1, …, n; s = 1, …, Nj; j = 1, …, k; 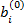 – константа модели для респондента с номером i, i = 1,…,n.
– константа модели для респондента с номером i, i = 1,…,n.
В маргинальной строке таблицы те же величины указаны без индексов i и характеризуют совокупность опрошенных респондентов в целом.
Поскольку модель (1) является регрессионной, то таблица 2, полученная на основе таблицы 1, исходные оценки можно переоценить. А именно объекту с номером l, характеристики которого имеют значения l1,l2,…, lk, lj ∈ {1,2,…,Nj}, j = 1,…,k, и респонденту с номером i, i = 1,…,n, ставится в соответствие новая величина  вычисляемая на основе (1):
вычисляемая на основе (1):
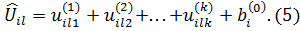
Величина  называется предсказанной полезностью объекта l для респондента i, l=1,…,K; i = 1,…,n. Кроме указанных величин, модель (1) позволяет оценить величину
называется предсказанной полезностью объекта l для респондента i, l=1,…,K; i = 1,…,n. Кроме указанных величин, модель (1) позволяет оценить величину
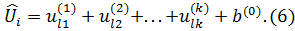
которая называется предсказанной полезностью товара l для всей совокупности опрошенных, l = 1,…,K. На основе (5) и (6) формируется таблица 3, аналогичная таблице 1.
Таблица 3. Представление предсказанных значений полезности.
| Варианты объектов | |||||
| Респондент | … | K | |||
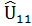 | 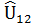 | 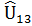 | … | 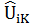 | |
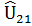 | 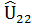 | 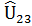 | … | 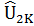 | |
| … | … | … | … | … | … |
| N | 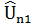 | 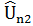 | 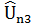 | … | 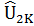 |
| Все | 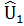 | 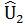 | 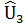 | … | 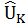 |
На основе модели (1) оценивается важность характеристик объекта.
Абсолютным вкладом характеристики j в полезность объекта называют величину Cj:
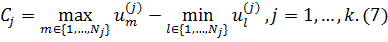
Для того чтобы вычислить значение Cj, j = 1,…,k, нужно рассмотреть ряд полезности значений характеристики j и вычислить разность его максимального и минимального элементов.
Совместным вкладом в полезность объекта называют величину C:
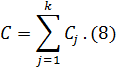
Относительным вкладом (важностью) характеристики j в полезность объекта называют величину RCj:
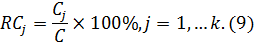
Для того, чтобы доказать, достаточно взять пару объектов L и M, которые отличаются только значением первой характеристики. Значения характеристик объекта L записываются как: (L, l2,…,lk), где 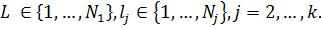 Значения характеристик объекта M записываются как: (M, l2,…,lk), где
Значения характеристик объекта M записываются как: (M, l2,…,lk), где 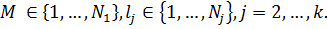 Тогда в силу (1) полезность объектов L и M отличается настолько, насколько отличаются полезности соответствующих значений первой характеристики:
Тогда в силу (1) полезность объектов L и M отличается настолько, насколько отличаются полезности соответствующих значений первой характеристики:
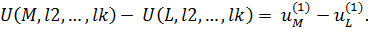
Предположим, что объект M по первой характеристике является максимально полезным, а объект L – минимально. Тогда полезность объектов L и М отличается на величину
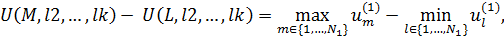
которая совпадает с величиной C1. Таким образом, величина C1 показывает, насколько можно изменить полезность всего объекта, меняя только первую характеристику, без изменения остальных.
Справедливо, что для любой величины Cj определенной формулой (7), изменение j-ой характеристики, покажет насколько можно изменить полезность всего объекта, меняя только одну характеристику.
Далее рассмотрим пару объектов, один из которых по всем характеристикам имеет наиболее полезные значения, а другой наименее. В соответствии с (1) разность полезности двух объектов:
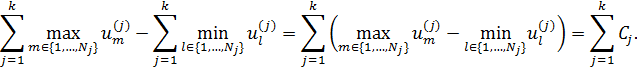
Таким образом, величина C, определяемая формулой (8), показывает, насколько можно изменить полезность объекта, меняя значение всех его характеристик. Использование относительных величин RCj, j = 1,…,k, придает сравнению атрибутов большую наглядность.
