Ошибка следящей системы при управлении по заданию и возмущению
Следящая система, система автоматического регулирования (управления), воспроизводящая на выходе с определённой точностью входное задающее воздействие, изменяющееся по заранее неизвестному закону. С. с. может иметь любую физическую природу и различные способы технического осуществления. Блок-схема (рис. 1) поясняет общий принцип действия С. с. Один из основных элементов С. с. — сравнивающее устройство, в котором производится сравнение фактически получающейся выходной величины х с заданной входной величиной g (t) и вырабатывается сигнал рассогласования e = g (t)—x. Передача величины х с выхода на вход осуществляется по цепи отрицательной обратной связи; при этом знак х меняется на обратный. Т. к. по заданию должно быть х = g (t), то рассогласование e является ошибкой С. с. Эта ошибка в хорошо работающей С. с. должна быть достаточно малой. Поэтому сигнал е усиливается и преобразуется в новый сигнал u, который приводит в действие исполнительное устройство. Исполнительное устройство изменяет х так, чтобы ликвидировать рассогласование. Однако из-за наличия различных возмущающих воздействий f (t) и помех n (t) рассогласование возникает вновь, и С. с. всё время работает на его уничтожение, т. е. «следит» за ним и, в итоге, за заданной величиной g (t). Для осуществления процесса управления с требуемой точностью применяют специальные корректирующие устройства, входящие в состав усилителя-преобразователя, и дополнительные местные обратные связи. В результате сигнал и достаточно сложным образом зависит от ей от параметров состояния самого исполнительного устройства. В некоторых случаях С. с. воспроизводят входную величину g (t) в др. масштабе x (t)= kg (t), где k — масштабный коэффициент, либо в соответствии с более сложной функциональной связью x (t)= = F [g (t)].
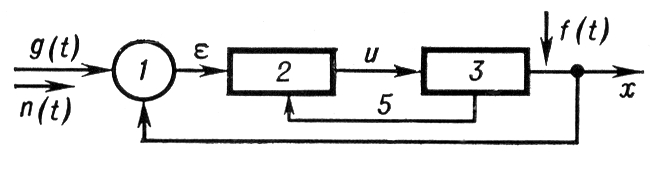
Процесс реализации компенсации возмущающего воздействия называется регулированием по возмущению. Регулирование по возмущению обладает достоинствами и недостатками. В числе достоинств следует отметить высокое быстродействие. К недостаткам нужно отнести то, что цепь компенсации обеспечивает необходимое качество регулирования только при действии того возмущения, на которое она рассчитана. При действии другого возмущения и необходимости компенсировать его действие нужно вводить новую цепь компенсации, что, конечно, усложняет систему. Цепь компенсации не является обратной связью, потому что по этой цепи передаётся входной сигнал, а не регулируемая (выходная) величина объекта . В системах, использующих принцип обратной связи или принцип регулирования по отклонению, решающее значение имеет сам факт отклонения регулируемой величины от установленной программы независимо от характера величины, вызвавшей это отклонение. Поэтому в системах автоматического регулирования по отклонению нет недостатка, имеющего место в системах регулирования по возмущению.
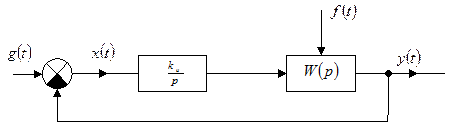
30. Повышение точности отработки управляющего воздействия за счёт повышения порядка астатизма. Повышение порядка астатизма используется для устранения установившихся ошибок в различных типовых режимах. Физически повышение порядка астатизма осуществляется за счет введения в канал регулирования интегрирующих звеньев.
Структурная схема регулирования с дополнительным интегрирующим звеном изображена на рис. 8.1
Передаточная функция интегрирующего звена:
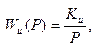
где − 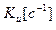 коэффициент передачи интегрирующего звена.
коэффициент передачи интегрирующего звена.
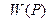 − передаточная функция разомкнутой системы до введения интегрирующего звена.
− передаточная функция разомкнутой системы до введения интегрирующего звена.
В качестве примера рассмотрим следящую систему множетельно-делительного устройства, изображенную на рис. 1.9. Для нее была получена передаточная функция разомкнутой системы в виде:
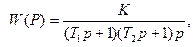 которая соответствует астатизму первого порядка. С целью повышения порядка астатизма введем в нее дополнительное последовательное интегрирующее звено (например, интегрирующий операционный усилитель) с передаточной функцией
которая соответствует астатизму первого порядка. С целью повышения порядка астатизма введем в нее дополнительное последовательное интегрирующее звено (например, интегрирующий операционный усилитель) с передаточной функцией 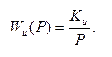
Тогда передаточная функция разомкнутой системы будет иметь вид: 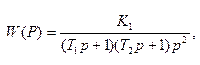
где 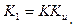 .
.
Так как порядок астатизма стал равен двум, то будет ликвидирована скоростная ошибка 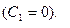
Сложив числитель и знаменатель W(P), получим характеристическое уравнение замкнутой системы: 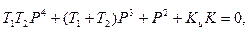 в котором коэффициент при P в первой степени равен нулю. Поэтому здесь не выполняется необходимое, но недостаточное условие устойчивости (все коэффициенты характеристического уравнения должны быть положительными) и система будет неустойчива при любых параметрах системы.
в котором коэффициент при P в первой степени равен нулю. Поэтому здесь не выполняется необходимое, но недостаточное условие устойчивости (все коэффициенты характеристического уравнения должны быть положительными) и система будет неустойчива при любых параметрах системы.
