Роль координатного метода в основной школе.

В школьной программе по математике методу координат уделяется мало внимания. По программе по математике для средней школы координаты появляются в 5 классе. Учащиеся знакомятся с координатами точки и изображением числа на прямой. В разных учебниках эти понятия вводятся по-разному. В учебнике по математике для 5 класса средней школы Виленкина в первой главе рассматривается координатный луч, затем, с его помощью, сравниваются натуральные и дробные числа. С понятием координатной прямой Виленкин знакомит учащихся в 6 классе. А вот в учебнике Дорофеева для 5 класса определение «координатный луч» не используется. Автор в начале 5 класса вводит понятие координатной прямой, еще до изучения отрицательных чисел, но учащиеся работают только с правой частью координатной прямой, которая и представляет собой координатный луч. В этом случае у учащихся могут возникнуть вопросы о другой части этой координатной прямой, что не совсем удобно. Так, в учебниках Виленкина содержится больше заданий, связанных с определением координатного луча, координатной прямой. Также автор чаще обращается к координатному лучу для введения других понятий, чем Дорофеев.

В программе по математике для средней школы в геометрии координаты изучаются в следующем объеме: координатная плоскость, формула расстояния между двумя точками плоскости, уравнение прямой и окружности.

В учебнике Погорелова «Геометрия для 7-11 классов средней школы» координаты занимают одно из основных мест. Они вводятся в 8 классе. Здесь, после рассмотрения основных понятий изучаются такие вопросы, как пересечение двух окружностей, пересечение прямой и окружности, определение синуса, косинуса и тангенса любого угла. Это первые приложения метода координат, с которыми ученики знакомятся в школе.

В учебнике Атанасяна «Геометрия для 7-9 классов средней школы» метод координат выделен в отдельную главу. В ней изучаются координаты вектора, уравнение прямой и окружности, решаются простейшие задачи в координатах. В этом учебнике метод координат дается как метод изучения геометрических фигур с помощью средств алгебры. Целью автора является не только обучение школьников применять метод координат к задачам на построение фигур по их уравнению, но и к задачам на доказательство и для вывода геометрических формул.

В учебнике Шарыгина «Геометрия 7-9 кл» уделяется больше внимания методам решения геометрических задач по сравнению с традиционными учебниками. Метод координат - предпоследняя тема 9 класса. При изучении этой темы ученики знакомятся с декартовыми координатами на плоскости, рассматривают уравнения прямой и окружности. Отметим, что в этом учебнике небольшой теоретический материал по данной теме. В отличие от учебников Атанасяна и Погорелова, формула середины отрезка у Шарыгина не рассматривается. Шарыгин не дает как такового понятия фигуры, но рассматривает уравнения «плоских линий», которые нужны для решения задач. После изучения векторов рассматривается параграф «Координатный метод». Учащимся предлагается ряд задач на данную тему. Это довольно сложные задачи, которые в основном связаны с нахождением геометрического места точек.

7.5 Различные способы задания плоскости в пространстве. Взаимное расположение двух плоскостей. Расстояние от точки до плоскости. Угол между двумя плоскостями. Методика изучения темы: «Параллельность прямых и плоскостей».

Способы задания плоскости в пространстве:

1) Общее уравнение плоскости: Ax+By+Cz+D=0

2) Параметрические уравнения плоскости: -плоскость, M₀ 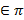, M₀(x₀, y₀, z₀) –точка, 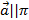, , 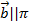(a₁, a₂, a₃), (b₁, b₂, b₃), а и b не параллельны, u и v – вещественные числа (параметры).

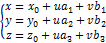
3) Уравнение плоскости, заданной точкой и двумя неколлинеарными векторами.

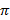- плоскость,M₀ 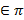, M₀(x₀, y₀, z₀) –точка, 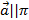, , 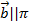(a₁, a₂, a₃), (b₁, b₂, b₃), а и b не параллельны.

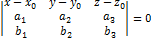
4) Уравнение плоскости, заданной тремя точками, не лежащими на одной прямой.

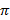-плоскость, M₁, M₂, M₃ 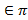М₁(х₁,y₁,z₁), М₂(х₂,y₂,z₂), М(х₃,y₃,z₃) не лежат на одной прямой.

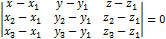
5) Уравнение плоскости в отрезках: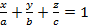

6) Уравнение плоскости, заданной точкой и вектором нормали

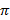- плоскость,M₀ 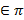, M₀(x₀, y₀, z₀) –точка, 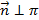, n(A,B,C)

A(x-x₀)+B(y-y₀)+C(z-z₀)=0.

7) Нормальное уравнение плоскости: α, β, γ - углы, которые составляет перпендикуляр, опущенный из начала координат на плоскость, с осями координат,p- длина перпендикуляра; xcosα+ycosβ+zcosγ=p.

Взаимное расположение двух плоскостей: две плоскости в пространстве либо параллельны, либо пересекаются.

1) Если две плоскости имеют общую точку, то они пересекаются по прямой.

Расположение прямых в пространстве: Две прямые в пространстве параллельны друг другу, пересекаются или скрещиваются.

2) Если две плоскости не имеют общих точек, то они параллельны друг другу.

Признак параллельности прямой и плоскости: Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости.

Т-ма (Расстояние от точки до плоскости).Если задана точка М(х₀, у₀ ), то расстояние до прямой Ах + Ву + С =0 определяется как d= .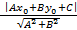

Док-во.Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁:d= 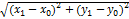(1)

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений: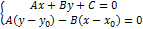

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М ₀ перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду:A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0,

то, решая, получим: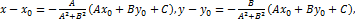

Подставляя эти выражения в уравнение (1), находим:d= 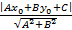.Теорема доказана.

Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможем найти угол. Точнее, косинус угла по формуле:cos = .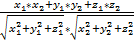