Методика обучения решению задач с помощью векторов в школьном курсе геометрии.
Тема начинает изучаться в 8 классе в курсе планиметрии. Вводится понятие вектора. Изучаются правила сложения и вычитания векторов. Дальнейшее изучение темы в 10 классе в курсе стереометрии: изучение векторов. 11 класс: в начале учебного года изучается метод координат.
При организации уроков-практикумов важно продумать систему вопросов к этапу анализа каждой задачи. Учащиеся должны осознать, какой прием использован при решении данной задач, как в дальнейшем можно использовать тот или иной факт.
Таким образом, учащиеся под руководством учителя должны выделить общий алгоритм решения задач для каждого из выделенных типов 1)-4). Например, чтобы решить задачу на перевод геометрического свойства фигуры на векторный язык, необходимо:
Записать векторное выражение, логически «вытекающее» из определения данного геометрического свойства, Записать равносильную задачу, Преобразовать с помощью законов векторной алгебры.
Важно обращать внимание учащихся на то, что одному и тому же геометрическому факту может соответствовать несколько векторных формул, но все эти соотношения равносильны между собой. При решении конкретной задачи следует выбирать ту векторную формулу, которая наиболее соответствует условию и требованию задачи.
При решении задач на преобразование векторных выражений требуется выполнить следующую последовательность действий: Раскрыть скобки, Сгруппировать векторы таким образом, чтобы к каждой паре векторов можно было применить или сложение векторов по правилу треугольника, или правило разности двух векторов с общим началом.
Для более эффективного выполнения учащимися данных типов упражнений необходимо составить с ними таблицы основных векторных формул и словарь перевода геометрических свойств фигур на векторный язык.
Так как задач, необходимых для успешного овладения выделенных умений, требуется решить достаточно много, то следует использовать принципы варьирования задач.
7.4Различные способы задания прямой на плоскости. Взаимное расположение двух прямых. Расстояние от точки до прямой. Угол между двумя прямыми. Роль координатного метода в основной школе.
Различные способы задания прямой.
1.Векторное (векторно-параметрическое) уравнение прямой.
Выберем на плоскости произвольную АСК О 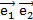 и зададим прямую
и зададим прямую 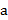 точкой М0 и направляющим вектором
точкой М0 и направляющим вектором 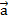 ,
, 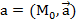 . "М
. "М 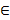 а
а 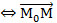 ||
|| 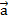 , но тогда
, но тогда 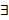 t
t 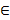 R:
R: 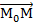 =t
=t  .
.
Пусть 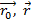 - радиус-векторы точек
- радиус-векторы точек 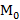 Î а и МÎа (рис.).
Î а и МÎа (рис.).
Тогда 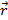 =
= 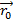 +t
+t  (
( 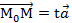 )
)
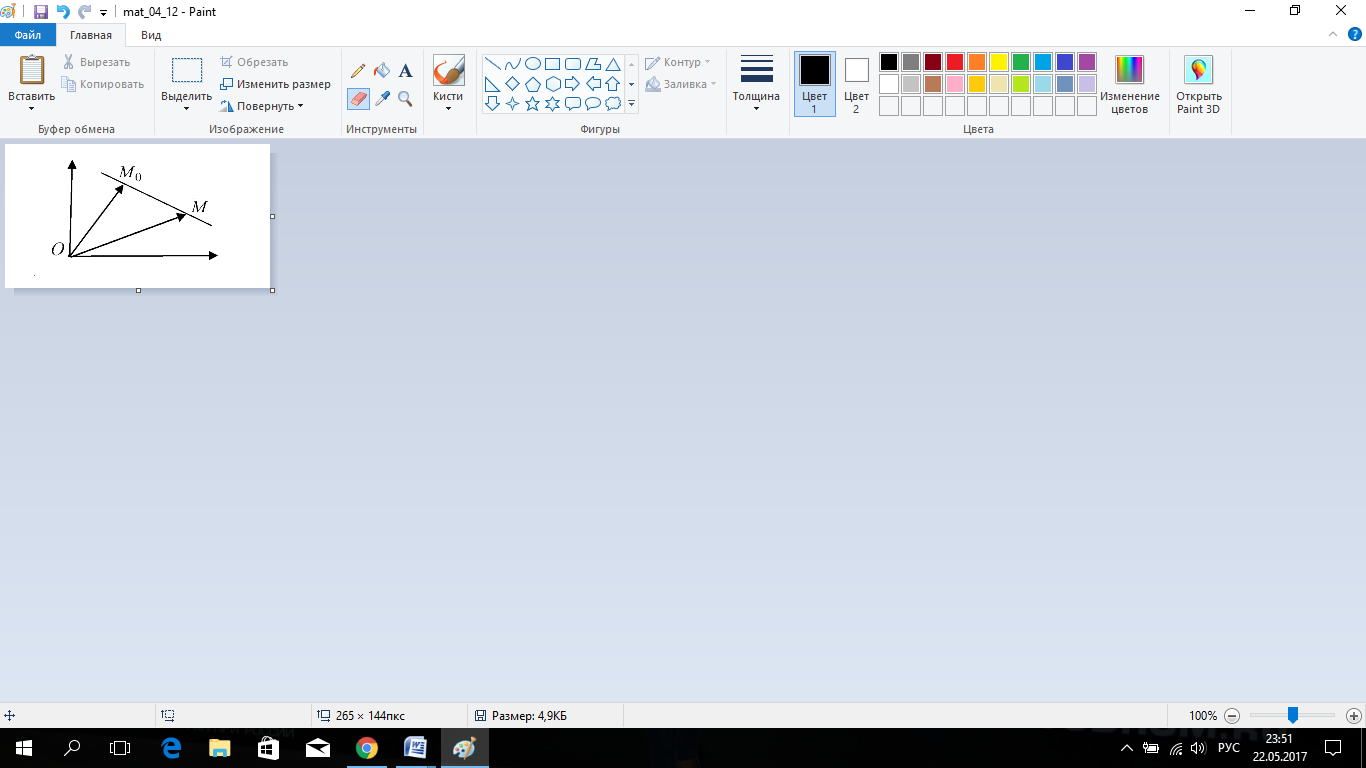
Данное уравнение наз.векторным или векторно-параметрическим ур.прямой, t-параметр.
2.Уравнение прямой, заданной точкой М0 и направляющим вектором 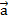 .
.
Пусть в АСК задана прямая а=( М0, 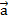 ), М0(х0,у0) ,
), М0(х0,у0) , 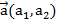 , М (х,у).
, М (х,у).
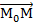 (х-х0, у-у0)
(х-х0, у-у0)
Так как 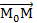 ||
|| 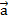 , то
, то 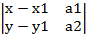 =0 или а2 (х-х0) – а1(у-у0) = 0.
=0 или а2 (х-х0) – а1(у-у0) = 0.
Полученные уравнения наз.уравнением прямой, заданной точкой и направляющим вектором.
Замечание: введем обозначения: А=а2, В= -а1, С= - а2х0+а1у0, тогда получим уравнение Ах+Ву+С=0, А2+В2≠0 ( 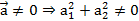 ).
).
Итак, уравнение любой прямой в АСК является уравнением первой степени, при этом вектор 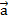 (-В,А) параллелен прямой а.
(-В,А) параллелен прямой а.
3. Общее уравнение прямой в АСК.
Т. Линия на плоскости, заданная в АСК ур.первой степени Ах+Ву+С=0, А2+В2≠0, есть прямая.
Док-во: необходимость следует из замечания (п.2). Достаточность: пусть линия на плоскости задана данным уравнением первой степени. Так как А2+В2≠0, то пусть для определенности А≠0, тогда А( 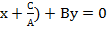 или
или 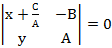 .
.
На плоскости существует М0( 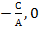 ) и
) и 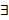
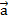 (-В,А),
(-В,А), 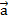 ≠0, но тогда сущ. прямая, а= (М0,
≠0, но тогда сущ. прямая, а= (М0, 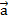 ) с направляющим вектором
) с направляющим вектором 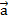 (-В,А)≠0 (
(-В,А)≠0 ( 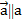 ). Ч.т.д.
). Ч.т.д.
Данное ур.наз. общим уравнением прямой.
4. Параметрические уравнения прямой.
Пусть в АСК прямая задана точкой М0 и направляющим вектором 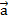 , при этом М0 (х0,у0),
, при этом М0 (х0,у0), 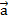 (а1, а2) и "МÎа: М(х,у).
(а1, а2) и "МÎа: М(х,у).
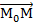 (х-х0, у-у0).
(х-х0, у-у0). 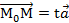 , тогда
, тогда 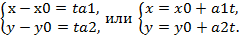
Полученные ур.наз.параметрическими ур.прямой, t-параметр.
5. Каноническое уравнение прямой.
Пусть в АСК прямая задана точкой М0 (х0,у0) и направляющим вектором 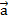 (а1, а2).
(а1, а2).
а) если а1≠0, а2≠0, то из п.4 следует 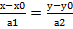 . Полученное уравнение наз.каноническим ур.прямой
. Полученное уравнение наз.каноническим ур.прямой
б) если а1=0 (а2≠0), то ур.прямой:х=х0;
если а2=0 (а1≠0), то ур.прямой: у=у0.
6. Уравнение прямой, заданной двумя точками.
Пусть в АСК О 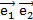 прямая задана двумя точками М1(х1, у1) и М2(х2,у2).
прямая задана двумя точками М1(х1, у1) и М2(х2,у2).
Тогда вектор 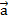 =
= 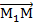 2 (х2-х1, у2-у1) – направляющий вектор прямой а. Для "М (х,у)Îа:
2 (х2-х1, у2-у1) – направляющий вектор прямой а. Для "М (х,у)Îа: 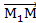 (х-х1, у-у1) ||
(х-х1, у-у1) || 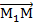 2, откуда
2, откуда 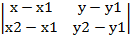 =0
=0
Если х2-х1≠0, у2-у1≠0, то получим уравнение 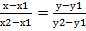 .
.
7.Уравнение прямой в отрезках.
Пусть в АСК прямая а 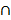 Ох=М1(а,0), а
Ох=М1(а,0), а 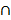 Оу=М2(0,b), точка О не принадлежит а. подставим координаты точек М1 и М2 в уравнение прямой п.6:
Оу=М2(0,b), точка О не принадлежит а. подставим координаты точек М1 и М2 в уравнение прямой п.6: 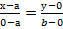 или
или 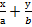 =1.
=1.
8. Уравнение прямой с угловым коэффициентом.
Пусть в АСК О 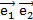 прямая задана М0 (х0,у0) и
прямая задана М0 (х0,у0) и 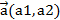 :
: 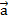 не ǁ
не ǁ 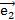 , но тогда координата а1≠0.
, но тогда координата а1≠0.
Число 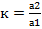 наз. Угловым коэффициентом прямой а.
наз. Угловым коэффициентом прямой а.
Т.Угловой коэффициент к прямой а не зависит от выбора направляющего вектора.
Так как 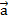 не ǁ
не ǁ 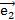 , то за точку М0 можно принять точку пересечения прямой а и Оу, т.е М0(0,b). Из ур. п2 получим:
, то за точку М0 можно принять точку пересечения прямой а и Оу, т.е М0(0,b). Из ур. п2 получим: 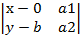 =0 или у=кх+b,
=0 или у=кх+b, 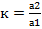 . Последнее уравнение и называют уравнением с угловым коэффициентом.
. Последнее уравнение и называют уравнением с угловым коэффициентом.
9. Уравнение прямой, заданной точкой и нормальным вектором.
Ненулевой вектор 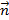 наз. перпендикулярным данной прямой а (нормальным вектором, вектором нормали), если он перпендикулярен любому направляющему вектору
наз. перпендикулярным данной прямой а (нормальным вектором, вектором нормали), если он перпендикулярен любому направляющему вектору 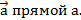
Обозначение: 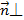 а.
а.
Если прямая а в ПДСК задана уравнением Ах+Ву+С=0, то 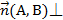 а.
а.
Т. Пусть в ПДСК О 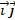 точка М0(х0,у0) Îа (а-прямая) и
точка М0(х0,у0) Îа (а-прямая) и 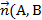 ) – нормальный вектор прямой а,
) – нормальный вектор прямой а, 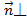 а, тогда ур. прямой а имеет вид: А(х-х0)+В(у-у0)=0.
а, тогда ур. прямой а имеет вид: А(х-х0)+В(у-у0)=0.
Док-во: Для "М(х,у) Îа: 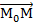 (х-х0; у-у0) ⏊
(х-х0; у-у0) ⏊ 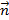 , но тогда:
, но тогда: 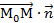 =0 или А(х-х0)+В(у-у0)=0. Ч.т.д.
=0 или А(х-х0)+В(у-у0)=0. Ч.т.д.
Данное ур.наз.уравнением прямой, заданной точкой и нормальным вектором.
10. Нормальное уравнение прямой.
Уравнение прямой в ПДСК: ax+by+c=0, 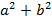 =1 наз. нормальным ур.прямой (или уравнением прямой в нормальной форме).
=1 наз. нормальным ур.прямой (или уравнением прямой в нормальной форме).
