Информация для человека — это знания, которые он получает из различных источников.

А.Н. Колмогоров(алфавитный подход): информация — это содержание последовательностей символов (сигналов) из некоторого алфавита.

Содержательный подход к измерению информации: Сообщение – информативный поток, который в процессе передачи информации поступает к приемнику. Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными. Информация - знания человека? сообщение должно быть информативно. Если сообщение не информативно, то количество информации с точки зрения человека = 0. (Пример: вузовский учебник по высшей математике содержит знания, но они не доступны 1-класснику).

Согласно Шеннону, информативность сообщения характеризуется содержащейся в нем полезной информацией – той частью сообщения, которая снимает полностью или уменьшает неопределенность какой-либо ситуации.

Неопределенность некоторого события – это количество возможных исходов данного события. Так, например, если из колоды карт наугад выбирают карту, то неопределенность равна количеству карт в колоде. При бросании монеты неопределенность равна 2.

Содержательный подход часто называют субъективным, так как разные люди информацию об одном и том же предмете оценивают по-разному.

Но если число исходов не зависит от суждений людей (случай бросания кубика или монеты), то информация о наступлении одного из возможных исходов является объективной.

Если сообщение уменьшило неопределенность знаний ровно в два раза, то говорят, что сообщение несет 1 бит информации.1 бит - объем информации такого сообщения, которое уменьшает неопределенность знания в два раза.

Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий. Тогда количество информации d, заключенное в этом сообщении, и число событий N связаны формулой: 2^d = N. Эта формула носит название формулы Хартли.

Формула Хартли: H = k log_аN, где k – коэффициент пропорциональности, а – основание системы меры. Формула Хартли не работает в случае различных состояний системы.

Пусть известны N состояний системы S, которые необходимо закодировать двоичным кодом. Вопрос: какой длины должен быть код? Число всех различных комбинаций из {0,1} длины d должно быть не меньше, чем N, т.е. 2^d≥N.

Прологарифмируем это неравенство: log₂2^d ≥ log₂N ⇒ d ≥ log₂N. Наименьшее решение этого неравенства называется мерой разнообразия множества состояний системы и задается формулой Хартли для двоичной системы счисления: H = log₂N (бит).

Модифицированная формула Хартли для неравновероятностных событий. Так как наступление каждого из N возможных событий имеет одинаковую вероятность p = 1 / N, то N = 1 / p и формула имеет вид : I = log₂N= log₂ (1/p) = - log₂ p

Количественная зависимость между вероятностью события (p) и количеством информации в сообщении о нем (I) выражается формулой: I = log₂(1/p)

Вероятность события вычисляется по формуле p=K/N, K – величина, показывающая, сколько раз произошло интересующее нас событие; N – общее число возможных исходов, событий. Если вероятность уменьшается, то количество информации увеличивается.

Алфавитный подход к измерению информации:Алфавитный подход основан на том, что всякое сообщение можно закодировать с помощью конечной последовательности символов некоторого алфавита.

Алфавит – упорядоченный набор символов, используемый для кодирования сообщений на некотором языке. Мощность алфавита – количество символов алфавита. Двоичный алфавит содержит 2 символа, его мощность равна двум. Сообщения, записанные с помощью символов ASCII, используют алфавит из 256 символов. Сообщения, записанные по системе UNICODE, используют алфавит из 65 536 символов.

С позиций computerscience носителями информации являются любые последовательности символов, которые хранятся, передаются и обрабатываются с помощью компьютера. Согласно Колмогорову, информативность последовательности символов не зависит от содержания сообщения, алфавитный подход является объективным, т.е. он не зависит от субъекта, воспринимающего сообщение. Чтобы определить объем информации в сообщении при алфавитном подходе, нужно последовательно решить задачи: Определить количество информации (d) в одном символе по формуле 2^d = N, где N - мощность алфавита.Определить количество символов в сообщении (m) Вычислить объем информации по формуле: V = d × m.

Все события происходят с различной вероятностью, но зависимость между вероятностью событий и количеством информации. Шеннон предложил связать количество информации в сообщении с вероятностью получения этого сообщения.

Вероятность – это количественная характеристика одного из исходов некоторого опыта, известная до его проведения. Измеряется в пределах от 0 до 1.

Теория Шеннона разработана как теория передачи данных по каналам связи, а мера Шеннона – как мера количества данных и не отражает семантического смысла.

Формула Шеннона дает оценку информации независимо от ее смысла: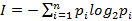

где n – число состояний системы; р_i – вероятность (относительная частота) перехода системы в i-е состояние (сумма всех p_i равна 1).