Глава 3. Функции нескольких переменных.

Определение.Если каждой паре независимых друг от друга чисел 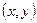из некоторого множества по какому-либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.

Определение.Областью определения функции z называется совокупность пар 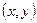, при которых функция z существует.

Область определения функции двух переменных 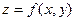представляет собой некоторое множество точек на координатной плоскости Oxy. Координата z называется аппликатой, и тогда сама функция изображается в виде некоторой поверхности в пространстве E³. Например:

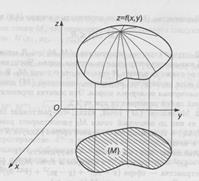
Рис.1

Частные производные.

Частная производная функции 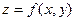по аргументу x является обыкновенной производной функции одной переменной x при фиксированном значении переменной y и обозначается:

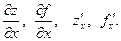
Частная производная функции 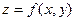по аргументу y является обыкновенной производной функции одной переменной y при фиксированном значении переменной x и обозначается:

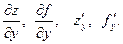
Пример 20.Найти частные производные функций.

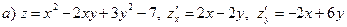
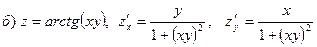
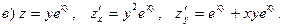
Частные производные второго порядка.

Частные производные второго порядка – это частные производные от частных производных первого порядка. Для функции двух переменных вида 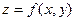возможны четыре вида частных производных второго порядка:

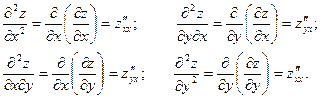
Частные производные второго порядка, в которых дифференцирование производится по разным переменным, называют смешанными производными. Смешанные производные второго порядка дважды дифференцируемой функции равны.

Пример 21.Найти частные производные второго порядка.

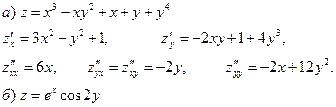
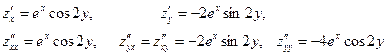
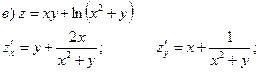
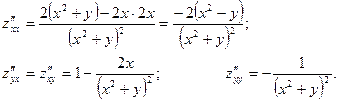
Дифференцирование неявной функции.

Определение.Функция 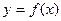называется неявной, если она задается уравнением 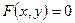, не разрешимым относительно y. Производная такой функции находится по формуле:

.

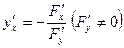Пример 22.Найти производные данных функций.

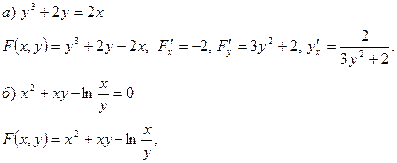
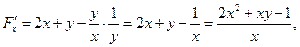
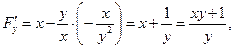
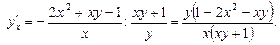
Локальный экстремум функции нескольких переменных.

Определение 1.Функция 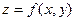имеет максимум в точке 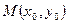, если 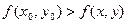для всех точек 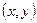достаточно близких к точке 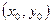и отличных от нее.

Определение 2.Функция 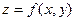имеет минимум в точке 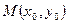, если 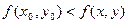для всех точек 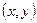достаточно близких к точке 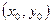и отличных от нее.

Необходимое условие экстремума.Если функция 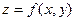достигает экстремума в точке 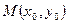, то частные производные от функции 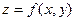обращаются в нуль или не существуют в этой точке.

Точки, в которых частные производные обращаются в нуль или не существуют, называются критическими.

Достаточный признак экстремума.Пусть функция 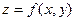определена в некоторой окрестности критической точки 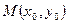и имеет в этой точке непрерывные частные производные второго порядка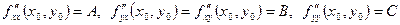

Тогда

1) 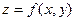имеет локальный максимум в точке 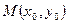, если 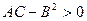и ;

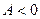2) 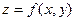имеет локальный минимум в точке 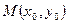, есл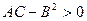и и ;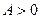

3) 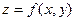не имеет локального экстремума в точке 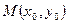, если ;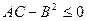