Мода и медиана случайной величины.

Мода случайной величины Mo – значение этой величины, имеющее наибольшую вероятность. Для распределения на многоугольнике – это x₂. Рассмотрение рисунка дает представление, откуда возникло понятие «пик моды». Например, высота каблука на туфлях – случайная величина (у разных людей может принимать разные значения), однако, некоторый размер встречается наиболее часто. Это модная высота каблука.

x
p	4/8	1/8	3/8

Для ряда распределения Mo = 4 (значение с наибольшей вероятностью).

Медиана случайной величины x Me – (такое ее значение, для которого одинаково вероятно, окажется ли случайная величина больше или меньше медианы.)

такое значение, что p (x<Me)= 1/2 . Для случайной величины то, что она окажется больше Me равновероятно с тем, что она окажется меньше ее. Для ряда распределения Me= 6 (хотя под требование подходит и любое число интервала (4 – 8).

Гипергеометрическое распределение.

Часто возникают задачи такого рода. Имеется N объектов, среди них M выделенных. Отбираем n объектов и изучаем случайную величину m – количество выделенных среди отобранных. Распределение такой случайной величины называется гипергеометрическим. Формула вероятности получена комбинаторными средствами:

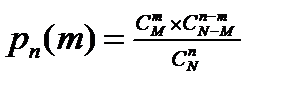
В знаменатели число всех возможных отборов n элементов, а в числителе – число способов отбора n элементов, когда m из них – выделенные.

Пример 1. На группу 22 юношей и 8 девушек дали 5 подарков. 4 подарка достались девушкам. Определить вероятность этого события при случайном розыгрыше. N=22 + 8 = 30, M = 8, n = 5, m = 4, далее по формуле: p₅ (4) =...

Пример 2. Известно, что среди 1000 билетов, участвующих в розыгрыше, 300 – выигрышных. Определить вероятность того, что из купленных пяти билетов: 1) ни один не выиграет; 2) выиграет ровно один. Здесь N = 1000, M = 300, n = 5, m = 0, 1, ...

Пример 3. В корзине 10 белых и 20 черных шаров. Определить вероятность того, что среди вытащенных 4-х не менее 2-х белых. Решение ненамного сложнее: p = p₄ (2) + p₄(3) + p₄ (4) = ...

Биномиальное распределение.

Случайное событие имеет вероятность p. Тогда вероятность того, что при n независимых испытаниях (вероятность одна и та же) оно наступит ровно m раз определяется:

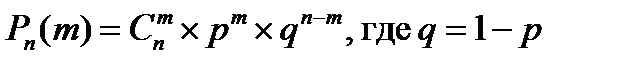
Случайная величина m – количество успехов в n независимых испытаниях имеет биномиальное распределение; p – вероятность успеха, q – неудачи. Биномиальным распределение называется потому, что вероятность является коэффициентами разложения бинома Ньютона: (p + q)ⁿ = p_n(0) + p_n(1) + ... + p_n(n).

1. В городе каждый четвертый автомобиль – иномарка. Определить вероятность того, что из пяти встречных автомобилей три окажутся иномарками.

p = 1/4, q = 3/4, m = 3, n = 5.

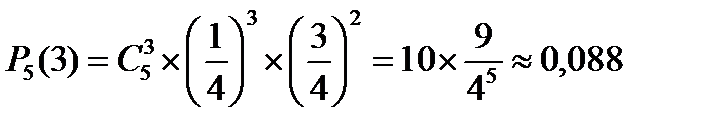
2. Вероятность при случайном блуждании по организации три раза подряд встретить женщину составляет 0,008. Определить долю мужчин в организации.

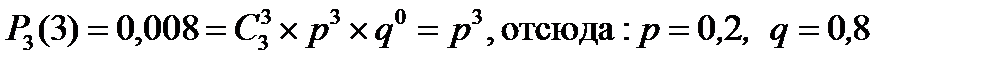
3. Шарики: 3 б + 2 ч. Вытаскиваем шар и кладем обратно (чтобы вероятность не менялась при следующем испытании – условие их независимости). Определить вероятность того, что из пяти попыток получим ровно 2 белых шара. Вероятность белого в каждой попытке одинакова p = 3/5; q = 2/5.

p₅(2) = 10 ´ (3/5)² ´ (2/5)³ = 720 / 5⁵

4. Известна вероятность того, что встречный человек – мужчина p = 0,6. Определить вероятность того, что из десяти встреченных людей трое будут мужчинами.

p₁₀(3) = (10!/(3! 7!)) ´ 0,6³ ´ 0,4⁷

5. Определить вероятность того, что событие из n попыток наступает хотя бы один раз. Заметим, что p_n(0) + p_n(1) + ... + p_n(n) = 1 (полная группа событий). Отсюда:

p(событие наступает от одного раза) = p_n(1) + ... + p_n(n)= 1 – p_n(0)= 1– qⁿ