Основные принципы и формулы комбинаторики.

Комбинаторика – раздел математики, который изучает методы подсчета числа различных комбинаций, почти всегда отвечает на вопрос: «Сколькими способами можно выполнить некоторое действие?».

Основные принципы.

1. Если действие состоит из двух операций, которые могут быть выполнены m и n способами соответственно, то общее число действий = m ´ n.

Шарики – 3 б + 2 ч. Сколькими способами можно выбрать пару б + ч? Действие можно разбить на две операции: выбор белого шарика (3 способа) и выбор черного (2 способа). Обще число способов выбора = 3 ´ 2 = 6 (этот же результат был получен в последней задаче).

На гору ведет 7 дорог. Сколько существует способов совершить прогулку на гору и обратно? Действие можно разбить на два: подъем на гору и спуск. Для любого выбранного способа подъема можно выбрать 7 способов спуска, всего 7 ´ 7 = 49 прогулок. А если потребовать не возвращаться по той же дороге, по которой поднялся? Для любого из 7 подъемов будет ровно 6 возможностей спуска, всего 7 ´ 6 = 42.

Карты (52). Число всех комбинаций карт вида («тройка»,«семерка»,«туз»)=4´4´4 (три операции: выбрать тройку, семерку и туза). Число всевозможных комбинаций из трех карт = 52 ´ 51 ´ 50 (три операции: выбрать первую, вторую, третью). Значит, вероятность вытащить комбинацию такого вида = 4´4´4 / 52 ´ 51 ´ 50.

Число четырехзначных чисел из цифр 0,1,2,3,4,5 = 5 ´ 6 ´ 6 ´ 6

Число нечетных ... = 5 ´ 6 ´ 6 ´ 3

... при условии, что цифры не повторяются = 5 ´ 5 ´ 4 ´ 3

2. Если действие выполняется любой одной из двух операций, которые могут быть выполнены m и n способами соответственно, то общее число действий = m + n.

Любая последовательность n различных объектов с учетом порядка называется перестановкой этих объектов.

Например, abc, acb, bac, bca, cab, cba – различные перестановки элементов abc.

Число всех возможных перестановок из n элементов:

P_n = n!

n! – арифметическая операция, читается n-факториал:

n! = 1 ´ 2 ´ 3 ´.... ´ n;

0! = 1.

Например, P₃ = 1 ´ 2 ´ 3 = 6, то есть можно было для его определения обойтись без перебора.

Действительно, как бы ни встали n–1 человек (одна операция), последний может разместиться среди них n способами (вторая операция), значит, из общего принципа комбинаторики: P_n = P_n–1 ´ n . Применяя многократно эту идею, и получим методом математической индукции доказательство формулы.

Например, 5 человек можно расставить в строю 5! = 1 ´ 2 ´ 3 ´ 4 ´ 5 = 120 способами.

Любое подмножество из m элементов множества, содержащего n элементов, называется сочетанием из n элементов по m.

Например, ab, ac, bc – сочетания из множества abc.

Число всех различных сочетаний из n элементов по m

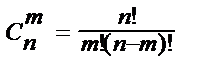
Например, число всех пар, которые можно выбрать из 5-ти шариков:

.

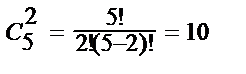Из пяти карточек с номерами 1, 2, 3, 4, 5 выбираются две. Определить вероятность того, что они окажутся соседними.

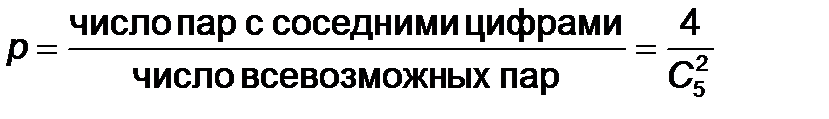
Построив таблицу сочетаний, можно обнаружить закономерность:

n	M

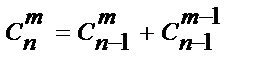Действительно, комбинации могут не содержать шарик n, а могут содержать, отсюда, по второму принципу комбинаторики, и два слагаемых.

Шарики – 3 б + 2 ч = 5. Определить вероятности того, что из двух выбранных оба белых, белый + черный, хотя бы один белый.

.

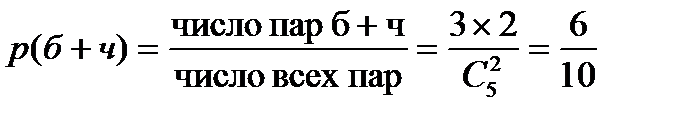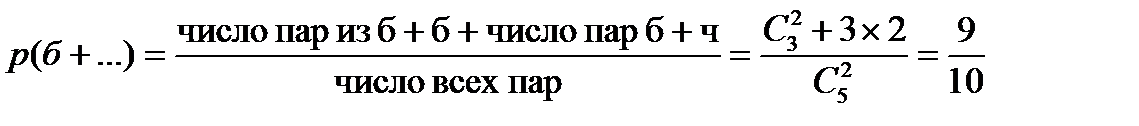
В общем виде, заменяя числа буквенными обозначениями, можно получить важную формулу, позволяющую решать многие комбинаторные задачи:

Шарики – N б + M ч = N + M. Определить вероятность того, что будет выбрана комбинация n белых + m черных.

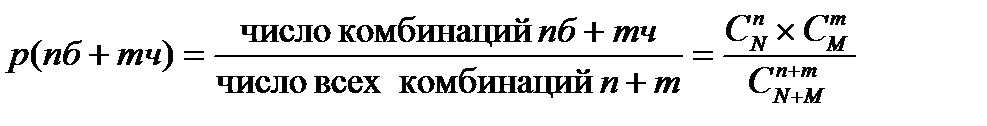
Использование формулы возможно, если удается отобразить условие задачи в задачу с шариками, то есть сопоставить шарикам объекты задачи.

Например, есть 10 вопросов. Из них учащийся знает 7. Какова вероятность того, что оба из двух вопросов билета окажутся известными? Здесь два типа объектов – известные и неизвестные вопросы. N = 7, M = 3, n = 2, m = 0. Подставляя в формулу, получим ответ 21 / 45, то есть вероятность чуть менее половины.