Дополнительный код (дополнение до двух)
Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. two's complement). Он же называется обратный дополнительный код.
Алгоритм получения дополнительного кода числа:
если число положительное, то в старший разряд записывается ноль, далее записывается само число;
если число отрицательное, то все биты модуля числа инвертируются, то есть все единицы меняются на нули, а нули — на единицы, к инвертированному числу прибавляется единица, далее к результату дописывается знаковый разряд, равный единице.
| Рис. 4. Нумерация двоичных чисел в представлении c дополнением до двух. |
 В качестве примера переведём число −5 в дополнительный восьмибитовый код. Прямой код модуля −5 — 0000101, обратный — 1111010, прибавляем 1, получаем 1111011, приписываем 1 в качестве знакового разряда, в результате получаем 11111011.
В качестве примера переведём число −5 в дополнительный восьмибитовый код. Прямой код модуля −5 — 0000101, обратный — 1111010, прибавляем 1, получаем 1111011, приписываем 1 в качестве знакового разряда, в результате получаем 11111011. Также дополнительный код отрицательного числа  , хранящегося в
, хранящегося в 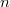 битах, равен
битах, равен  . По сути, дополнительный код представляет собой дополнение
. По сути, дополнительный код представляет собой дополнение  до
до  : так как в
: так как в 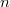 -разрядной арифметике
-разрядной арифметике  (двоичная запись этого числа состоит из единицы и
(двоичная запись этого числа состоит из единицы и 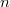 нулей, а в
нулей, а в 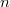 -разрядную ячейку помещаются только
-разрядную ячейку помещаются только 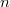 младших разрядов, то есть
младших разрядов, то есть 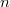 нулей), то верно равенство
нулей), то верно равенство  .
.
Для получения из дополнительного кода самого числа нужно инвертировать все разряды кода и прибавить к нему единицу. Можно проверить правильность, сложив дополнительный код с самим числом: результат должен быть равен 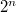 . Переведём 11111011 обратно. Инвертируем — 00000100, прибавляем 1, получаем 00000101 — модуль исходного числа −5. Проверим: 11111011 + 00000101 = 100000000.
. Переведём 11111011 обратно. Инвертируем — 00000100, прибавляем 1, получаем 00000101 — модуль исходного числа −5. Проверим: 11111011 + 00000101 = 100000000.
Можно получить диапазон значений 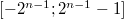 .
.
Достоинства метода:
· возможность заменить арифметическую операцию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, что существенно упрощает архитектуру процессора и увеличивает его быстродействие;
· нет проблемы двух нулей.
Недостатки: ряд положительных и отрицательных чисел несимметричен, но это не так важно: с помощью дополнительного кода выполнены гораздо более важные вещи, желаемые от способа представления целых чисел.
Арифметические действия над целыми числами
Обратный и дополнительный коды применяются особенно широко, так как они позволяют упростить конструкцию арифметико-логического устройства (АЛУ) компьютера путем замены некоторых арифметических операций сложением.
Обычно десятичные числа при вводе в машину автоматически преобразуются в двоичный код (целые без знака), обратный или дополнительный код (целые со знаком) и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе результатов из машины происходит обратное преобразование в десятичные числа.
Сложение и вычитание
Сложение и вычитание чисел без знака происходит по обычным для позиционных систем счисления алгоритмам.
Примеры (для k =3):
0012+1002= 1012;
1012-0102=0112.
Ситуации, когда уменьшаемое меньше вычитаемого или когда результат суммы не умещается в k разрядов, считаются ошибочными и должны отслеживаться устройством компьютера. Реакция на такие ошибки может быть различной в разных типах компьютеров.
