Как найти фундаментальную систему решений линейного уравнения?

Возьмём для примера такую систему линейных уравнений:

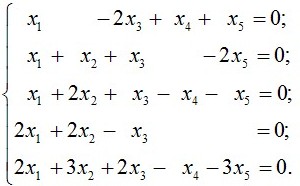
Найдём решение этой линейной системы уравнений методом Гаусса. Для начала нам надо выписать матрицу коэффициентов системы.

Преобразуем эту матрицу к треугольной. Первую строку переписываем без изменений. И все элементы, что стоят под a11, надо сделать нулями. Что бы сделать ноль в место элемента a21, надо от второй строки вычесть первую, и разность записать во второй строке. Что бы сделать ноль в место элемента a31, надо от третьей строки вычесть первую и разность записать в третьей строке. Что бы сделать ноль в место элемента a41, надо от четвёртой строки вычесть первую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента a31, надо от пятой строки вычесть первую умноженную на 2 и разность записать в пятой строке.

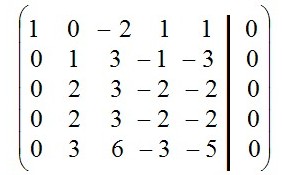
Первую и вторую строку переписываем без изменений. И все элементы, что стоят под a22, надо сделать нулями. Что бы сделать ноль в место элемента a32, надо от третьей строки вычесть вторую умноженную на 2 и разность записать в третьей строке. Что бы сделать ноль в место элемента a42, надо от четвёртой строки вычесть вторую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента a52, надо от пятой строки вычесть вторую умноженную на 3 и разность записать в пятой строке.

Видим, что последние три строки – одинаковые, поэтому если от четвёртой и пятой вычесть третью, то они станут нулевыми.

По этой матрице записываем новую систему уравнений.

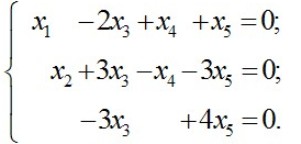
Видим, что линейно независимых уравнений у нас, только три, а неизвестных пять, поэтому фундаментальная система решений будет состоять из двух векторов. Значит, нам надо перенести две последние неизвестные вправо.

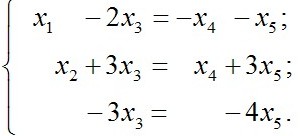
Теперь, начинаем выражать те неизвестные, что стоят в левой части через те, что стоят в правой части. Начинаем с последнего уравнения, сначала выразим x3, потом полученный результат подставим во второе уравнение и выразим x2, а потом в первое уравнение и тут выразим x1. Таким образом мы все неизвестные, что стоят в левой части, выразили через неизвестные, что стоят в правой части.

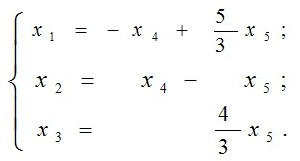
После чего вы вместо x4 и x5, можем подставлять любые числа и находить x1, x2 и x3. Каждая такая пятёрка чисел будет корнями нашей изначальной системы уравнений. Что бы найти векторы, что входят в ФСР нам надо вместо x4 подставить 1, а вместо x5 подставить 0, найти x1, x2 и x3, а потом наоборот x4=0 и x5=1.

Какие именно векторы создают фундаментальную систему решений данной системы уравнений?

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 16

1. Действия над матрицами. Обратная матрица. Матричные уравнения.

http://www.studfiles.ru/preview/5680005/

http://greleon.ru/vishmath/lekcii/173-lekciya-matricy-osnovnye-vidy-matric-deystviya-nad-matricami.html

http://www.grandars.ru/student/vysshaya-matematika/obratnaya-matrica.html

Обратная матрица

Пусть имеется квадратная матрица n-го порядка

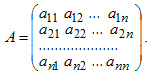
Матрица А^-1 называется обратной матрицей по отношению к матрице А, если А*А^-1 = Е, где Е — единичная матрица n-го порядка.

Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:

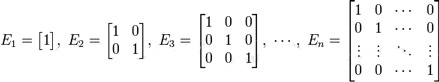
Обратная матрица может существоватьтолько для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.