Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность.

Теорема Кронекера-Капелли

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. rangA=rangA˜.

Система называется совместной, если она имеет хоть одно решение. Теорема Кронекера-Капелли говорит вот о чём: если rangA=rangA˜, то решение есть; если rangA≠rangA˜, то данная СЛАУ не имеет решений (несовместна). Ответ на вопрос о количестве этих решений даёт следствие из теоремы Кронекера-Капелли. В формулировке следствия использована буква n, которая равна количеству переменных заданной СЛАУ.

Следствие из теоремы Кронекера-Капелли

1. Если rangA≠rangA˜, то СЛАУ несовместна (не имеет решений).

2. Если rangA=rangA˜<n, то СЛАУ является неопределённой (имеет бесконечное количество решений).

3. Если rangA=rangA˜=n, то СЛАУ является определённой (имеет ровно одно решение).

Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения нет, а если существуют – то сколько.

Методы решения СЛАУ

1. Метод Крамера

Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода Крамера можно выразить в трёх пунктах:

1. Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. Δ≠0.

2. Для каждой переменной xi необходимо составить определитель Δ X_i, полученный из определителя Δ заменой i-го столбца столбцом свободных членов заданной СЛАУ.

3. Найти значения неизвестных по формуле xi= Δ X_i /Δ

Решение систем линейных алгебраических уравнений с помощью обратной матрицы.

Решение систем линейных алгебраических уравнений (СЛАУ) с помощью обратной матрицы (иногда этот способ именуют ещё матричным методом или методом обратной матрицы) требует предварительного ознакомления с таким понятием как матричная форма записи СЛАУ. Метод обратной матрицы предназначен для решения тех систем линейных алгебраических уравнений, у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода обратной матрицы можно выразить в трёх пунктах:

1. Записать три матрицы: матрицу системы A, матрицу неизвестных X, матрицу свободных членов B.

2. Найти обратную матрицу A^-1.

3. Используя равенство X=A^-1⋅B получить решение заданной СЛАУ.

Метод Гаусса. Примеры решения систем линейных алгебраических уравнений методом Гаусса.

Метод Гаусса является одним из самых наглядных и простых способов решения систем линейных алгебраических уравнений (СЛАУ): как однородных, так и неоднородных. Коротко говоря, суть данного метода состоит в последовательном исключении неизвестных.

Преобразования, допустимые в методе Гаусса:

1. Смена мест двух строк;

2. Умножение всех элементов строки на некоторое число, не равное нулю.

3. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.

4. Вычеркивание строки, все элементы которой равны нулю.

5. Вычеркивание повторяющихся строк.

Насчет последних двух пунктов: повторяющиеся строки можно вычёркивать на любом этапе решения методом Гаусса, – естественно, оставляя при этом одну из них. Например, если строки №2, №5, №6 повторяются, то можно оставить одну из них, – например, строку №5. При этом строки №2 и №6 будут удалены.

Нулевые строки убираются из расширенной матрицы системы по мере их появления.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 15

1. Преобразование матрицы линейного оператора при смене базиса.

http://www.math.mrsu.ru/text/courses/method/preobraz.htm

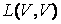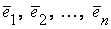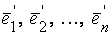Пусть V – линейное пространство, А – линейный оператор из , и – два базиса в V и 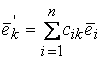– формулы перехода от базиса 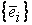к базису 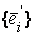. Обозначим через 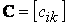матрицу перехода от базиса к базису. Отметим, что ранг матрицы С равен n. Пусть 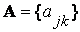и 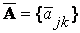– матрицы оператора А в указанных базисах.

Теорема 7.1. Матрицы А и 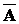оператора А в базисах 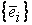и 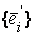связаны соотношением .

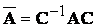Доказательство. При воздействии линейного оператора А вектор 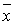пространства 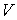переводится в вектор 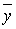этого пространства, т.е. справедливо равенство

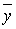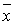= А (7.3)

(в старом базисе) и равенство

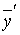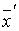= А (7.4)

(в новом базисе). Так как 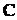– матрица перехода от старого базиса к новому, то

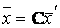(7.5)

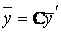(7.6)

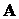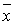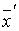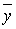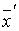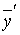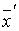Умножим равенство (7.5) слева на матрицу , получим А = АC и с учетом (7.3) = АC . Заменив левую часть полученного выражения в соответствии с (7.6), получим: С = АC или 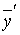= С^–1 АC 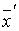. Сравнивая найденное выражение с равенством (7.4), получим доказываемую формулу.

Отсюда следует, что определитель матрицы линейного оператора не зависит от базиса.

2. Построение фундаментальной системы решений и общего решения однородной системы линейных уравнений.

http://matemonline.com/primeru/fsr/

Фундаментальная система решений (конкретный пример)

Вы можете заказать подробное решение вашей задачи здесь!!!

Чтобы понять, что такое фундаментальная система решений вы можете посмотреть видео-урок для этого же примера кликнув здесь. Теперь перейдем собственно к описанию всей необходимой работы. Это поможет вам более детально разобраться в сути данного вопроса.