Распределение касательных напряжений в сечениях балок различной формы.

Прямоугольное сечение. Найдем касательное напряжение, для чего проведем горизонтальный разрез на уровне (рис 11.3,а)

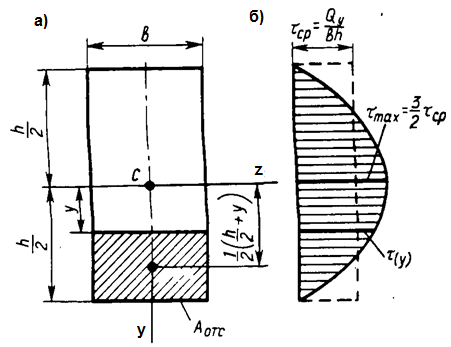
Рис. 11.3 Распределение касательных напряжений

в прямоугольном сечении балки

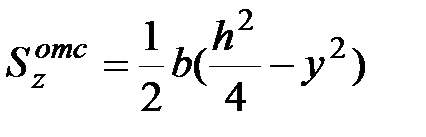(11.6)

Подставим (11.6) в (11.4) в результате получим:

,

,

,

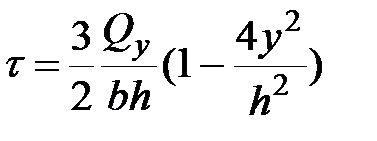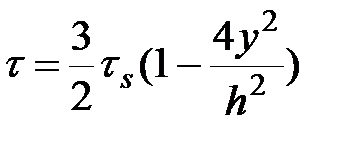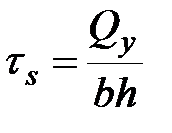(11.6)

где - среднее напряжение в сечении.

Эпюра показана на рис. 11.3,б. В крайних точках сечения 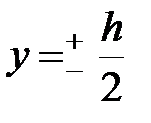, . Это согласуется с законом парности касательных напряжений, т.к. на поверхности бруса касательных напряжений нет.

Толстостенный двутавр (рис. 11.4,а).При составлении выражения для 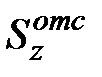следует рассмотреть два случая:1) 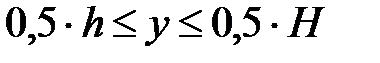(широкая часть сечения); 2)(узкая часть сечения)

Рис. 11.4 Изменение погонного сдвигового усилия и напряжений по высоте толстостенного двутавра при изгибе

В первом случае по аналогии с прямоугольным сечением:

,

(11.7)

Во втором случае

.

(11.7)

Выражения(11.5) для погонной сдвигающей силы примут вид:

,

,

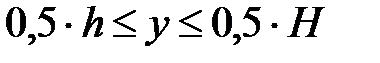(11.8)

Аналогично для второго случая:

(11.9)

Эпюры показаны на рис 11.4,б. Касательные напряжения соответственно определятся так: 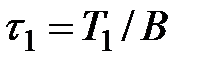, 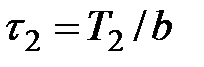. Эпюры напряжений на рис 11.4,в.

Двутавр.Двутавровое сечение может быть представлено в виде сопряжений трех прямоугольников: двух горизонтальных полок и вертикальной стенки (рис.11.5).

Рис. 11.5 К определению касательных напряжений в балке двутаврового сечения

Напряжения в стенкеопределяться по формуле (см. 11.4)

,

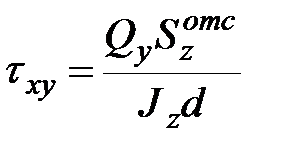(11.10)

где 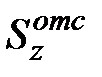- вычисляется для заштрихованной части сечения, показанной на рисунке 11.5. Наибольшие значения касательные напряжения имеют на уровне нейтральной оси при y=0.

,

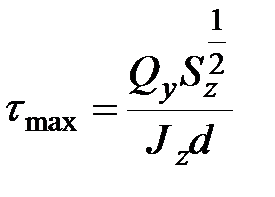(11.11)

где 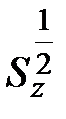- статический момент половины площади сечения относительно оси z

.

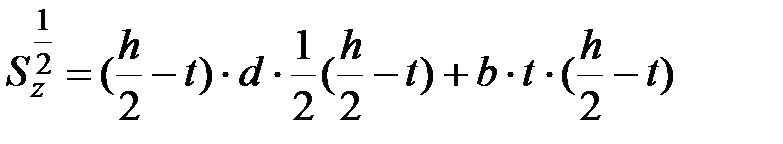(11.12)

Для прокатных двутавров и швеллеров величина статического момента половины сечения приведена в сортаменте.

На уровне сопряжения полки и стенки касательные напряжения определяются по формуле

,

.

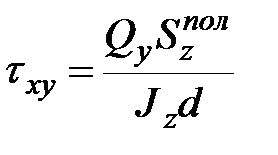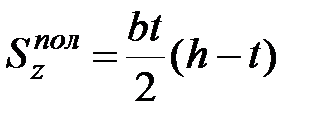(11.13)

Напряжения в полках не могут быть найдены по формуле (11.4), так как и предположение о равномерном их распределении по ширине полки становится неприемлемым. Напряжения в полках малы и не представляют практического интереса.

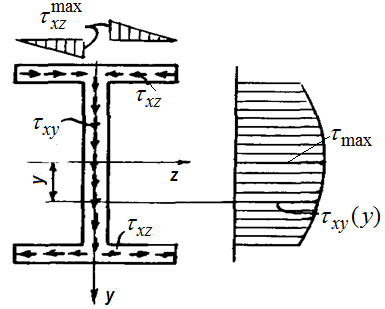
Рис. 11.6 Касательные напряжения в полках и стенке двутавра

Значительными являются горизонтальные напряжения 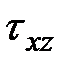в полках (рис. 11.6). Для определения этих напряжений рассмотрим равновесие бесконечно малого элемента, выделенного из нижней полки.

Согласно закону парности касательных напряжений на продольной грани этого элемента действуют напряжения 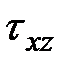(рис 11.7,а, б). Вследствие малости толщины полки двутавра эти напряжения можно считать равномерно распределенными по толщине полки . С учетом этого можно записать уравнение равновесия и определить :

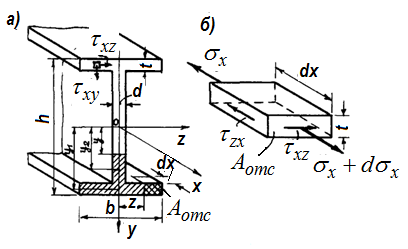
Рис. 11.7 К определению касательных напряжений

,

.

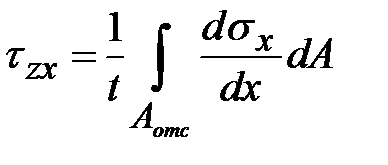(11.14)

Во второе уравнение (11.14) подставим выражение для 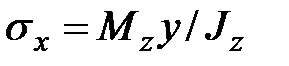и с учетом , получим

.

(11.15)

Учитывая, что и 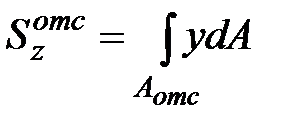будем иметь:

,

.

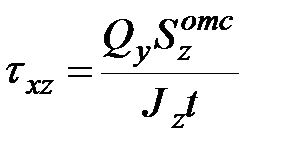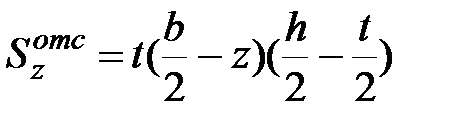(11.16)

Из формул (11.16) видно, что касательные напряжения по оси Оz (вдоль полки) изменяются по линейному закону. На рис. 11.6 показаны эпюры касательных напряжений .

Касательные напряжения образуют в сечении двутавра непрерывный поток, направленный в каждой точке параллельно контуру сечения.