Операции с векторами и матрицами
В MATLAB имеется ряд встроенных функций, позволяющих формировать векторы и матрицы определенного вида. Перечислим некоторые из них:
eye(m, n) — возвращают единичную матрицу размера m x n с единицами по диагонали и нулями в остальных ячейках;
ones(m, n) — возвращают матрицу размера m x n, состоящую из единиц;
zeros(m, n) — возвращают матрицу размера m x n, состоящую из нулей;
linspace(a, b, n) — генерирует n точек, равномерно распределенных в интервале от а до b;
rand(m, n) — генерирует матрицу случайных чисел размера m x n из промежутка (0, 1), используя равномерный закон распределения; rand () без аргументов возвращает одно случайное число;
В приведенных выше функциях (кроме linspace( n)) в качестве аргумента допустимо использовать size(A), что позволит формировать результирующую матрицу того же размера и размерности, что и А.
cat (dim, А, В) — реализует конкатенацию (объединение) массивов А и В в соответствии со спецификацией размерности dim и возвращает объединенный массив. При этом, при dim = 1 происходит горизонтальная конкатенация, при dim = 2 — вертикальная.
X = diag(v) — помещает вектор v на главную диагональ квадратной матрицы X и нули в остальные ячейки;
v = diag(X) — возвращает главную диагональ матрицы X;
repmat (А, m, n) — возвращает матрицу В размера m x n, в которой каждый элемент заменяется на копию матрицы А); если А — скаляр, то функция возвращает матрицу размера m x n со значениями элементов, заданных А;
tril(X, k) — возвращает матрицу, все элементы которой, расположенные выше k-й диагонали, заменены нулями, а нижняя треугольная часть матрицы X, включая указанную диагональ, остается неизменной. При k=0 это главная диагональ, при k>0 — одна из верхних диагоналей, при k<0 — одна из нижних диагоналей. По умолчанию к = 0.
triu(X. k) — возвращает неизменной верхнюю треугольную часть матрицы X, начиная с k-й диагонали, остальные элементы заменяются нулями. При k=0 — это главная диагональ, при k>0 — одна из верхних диагоналей, при k<0 — одна из нижних диагоналей;
magic(n) – возвращает так называемый магический квадрат – квадратную матрицу размера n x n, в которой сумма значений элементов по строкам, столбцам, а также сумма элементов главной и побочной диагонали равны.
Помимо перечисленных функций в системе имеется еще ряд встроенных функций для операций над векторами и матрицами:
prod (A, dim) — возвращает произведение элементов массива А по столбцам при dim=l или по строкам при dim=2;
sum(A, dim) — возвращает сумму элементов массива A по столбцам (dim=1) или по строкам (dim=2).
cross(U, V) — возвращает векторное произведение векторов U и V в трехмерном пространстве;
dot(U, V) — возвращает скалярное произведение векторов U и V;
transpose(X) – транспонирование вектора/матрицы Х;
trace(X) – возвращает след матрицы Х, т. е. сумму ее диагональных элементов;
isequal(U ,V) – проверка равенства векторов/матриц U и V;
norm(X, dim) – возвращает норму вектора Х, при dim=1 – первую норму ( 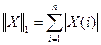 ), при dim=2 – евклидову (вторую) норму (
), при dim=2 – евклидову (вторую) норму ( 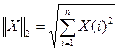 ), при dim=3 – бесконечную норму(
), при dim=3 – бесконечную норму( 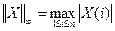 );
);
det(X) – возвращает определитель матрицы X;
inv(X) – возвращает матрицу, обратную к матрице X;
rank (X) – возвращает ранг матрицы X.
Весьма представителен в MATLAB набор матричных функций. Перечислим некоторые из них:
ехрт(Х) — возвращает 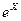 от матрицы X;
от матрицы X;
sqrtm(X) – возвращает логарифм матрицы;
logm(X) – возвращает квадратный корень из X, соответствующий неотрицательным действительным частям собственных значений X.
ЧИСЛЕННЫЕ МЕТОДЫ
