Методические указания и решение ситуации

Количественными характеристиками межличностных отношений являются социометрические индексы, которые можно разделить на два класса. Первый класс - персональные социометрические индексы, отражающие индивидуальные социально-психологические свойства личности, проявляющиеся в отношении к членам группы. Второй класс - групповые индексы, характеризующие группу в целом.

Таблица 8.2

ГРУППОВАЯ СОЦИОМЕТРИЧЕСКАЯ МАТРИЦА

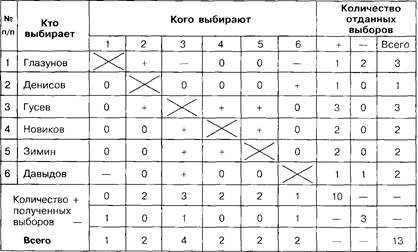
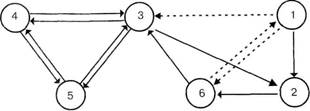
Структура анализируемых групповых отношений может быть наглядно представлена и в графической форме, в виде социограммы (рис. 8.1). Визуальный анализ социограммы позволяет судить о сложившихся взаимоотношениях в группе в аспекте того, как члены группы выбирают и кого, кто более активно выбирается, кто чаще отвергается.

Представленная социограмма может быть упрощена (и соответственно, упрощен проводимый анализ групповых отношений), если отдельно представить существующие «положительные» (рис. 8.2) и «отрицательные» (рис. 8.3) связи.

По количеству отданных выборов можно судить о степени и характере потребности отдельных членов и группы в целом в общении. В нашем примере члены группы, стоящие в списке под № 1, 3-6, проявляют умеренную потребность в общении (два-три отданных выбора из пяти возможных). Денисов (№ 2) обнаруживает по результатам анализа наименьшую потребность в общении.

- положительное отношение;

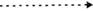- отрицательное отношение;

- взаимоположительное отношение;

- взаимоотрицательное отношение.

Рис. 8.1. Социограмма групповых отношений

Рис. 8.2. Положительные выборы по критерию

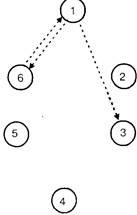
Рис. 8.3. Отрицательные выборы по критерию

По количеству полученных выборов можно судить о характере и степени влияния того или иного члена группы на других коллег по работе.

Используя данные табл. 8.2 и социограммы, можно сделать вывод о том, что наивысшим статусом в группе обладает Гусев (№ 3) - три положительных выбора. Члены группы - Гусев, Новиков и Зимин образуют неформальную группу, выбирая друг друга. Глазунов (№ 1) и Давыдов (№ 6) испытывают взаимную неприязнь. Из социограммы видно, что в сложившихся отношениях сотрудники (№ 2, 3 и 6) могут работать в единой рабочей группе, так как имеют замкнутый контур положительных выборов. Единая рабочая группа с учетом сложившихся отношений не может быть сформирована из сотрудников № 1, 3 и 6.

Сплоченность группы может быть охарактеризована соотношением положительных, отрицательных и нейтральных выборов. Используя исходные данные, можно получить следующие соотношения.

Всего получено выборов по группе	В том числе
положительных	отрицательных	нейтральных
шт.	%	шт.	%	шт.	%	шт.	%

По полученным результатам группа характеризуется средней степенью сплоченности (57% составляют нейтральные выборы и только 33% положительных выборов).

Интегральную характеристику сплоченности в группе можно получить с помощью индекса сплоченности группы (I_гр). Он рассчитывается как отношение разности взаимоположительных и взаимоотрицательных выборов по группе к общему количеству всех возможных выборов:

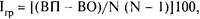
где ВП - число взаимоположительных выборов в группе; ВО - число взаимоотрицательных выборов в группе; N - число членов группы, участвовавших в опросе.

В нашем примере

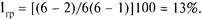
Полученное значение I_гр подтверждает ранее сделанный вывод о невысоком уровне сплоченности группы:

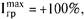
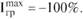
Анализ уровня связанности группы по выделенному критерию следует проводить, используя индекс социометрической когерентности (I_ког). Данный индекс можно рассчитать как отношение количества отданных (или полученных) выборов к общему количеству всех возможных выборов:

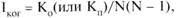
где К_о - число отданных выборов по группе;

К_п - число полученных выборов по группе;

N - число членов группы, участвовавших в опросе.

В нашем примере

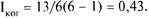
Сплоченность группы может быть изменена с помощью индекса взаимности (I_в). Сплоченность группы проявляется прежде всего в количестве взаимоположительных связей, поэтому индекс сплоченности рассчитывается по формуле

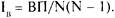
В нашем примере

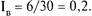
Это невысокое значение межгрупповой взаимности.

Наиболее распространенными персональными социометрическими индексами являются социометрический статус члена группы, индекс эмоциональной экспансивности и индекс объема взаимодействия.

Социометрический статус (C_i) отражает отношение членов группы к каждому ее представителю:

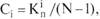
где 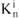- количество голосов (выборов), полученных i-м членом группы.

Одновременно принято исчислять положительный и отрицательный статусы, являющиеся частями общего социометрического статуса индивида:

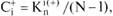
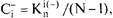
где 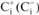- положительный (отрицательный) социометрический

статус i-го члена группы;

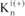- количество положительных выборов, полученных i-м членом группы;

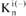- количество отрицательных выборов, полученных i-м членом группы.

Для характеристики степени активности каждого члена группы, его отношения к окружающим можно использовать индекс эмоциональной экспансивности (Ё₍), исчисляемый по формуле

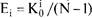
где 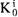- количество выборов (голосов), отданных i-м членом

группы.

Аналогично рассчитываются индексы положительной и отрицательной экспансивности:

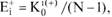
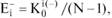
где 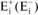- положительный (отрицательный) индекс эмоциональной экспансивности;

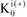- количество положительных выборов, отданных i-м членом группы;

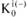- количество отрицательных выборов, отданных i-м членом группы.

Дополняет эти социометрические показатели индекс объема взаимодействия (А_;), который характеризует каждого члена группы одновременно и как субъекта выбора, и как объекта:

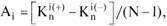
где 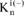- количество положительных выборов, полученных i-м членом группы;

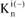- количество отрицательных выборов, полученных i-м членом группы.

В табл. 8.3 приведены расчетные значения указанных выше персональных социометрических индексов для нашего примера.

Если расположить полученные значения индекса взаимности членов группы в порядке убывания, то можно сформировать относительные оценки авторитетности.

Социометрические соотношения довольно динамичны вследствие изменчивости отношений людей, их взглядов, восприятия происходящих событий и т.д. В этой связи не следует абсолютизировать возможности и результаты социометрического анализа. Их следует рассматривать как первичную информацию для более содержательного анализа отношений в рабочем коллективе.

Таблица 8.3

ЗНАЧЕНИЯ ПЕРСОНАЛЬНЫХ СОЦИОМЕТРИЧЕСКИХ ИНДЕКСОВ

№ п/п	Члены группы	Социометрический статус	Эмоциональная экспансивность	Индекс объема взаимодействия
положительный	отрицательный	общий	положительная	отрицательная	общая
	Глазунов		0,2	0,2	0,2	0,4	0,6	-0,2
	Денисов	0,4		0,4	0,2		0,2	+0,4
	Гусев	0,6	0,2	0,8	0,6		0,6	+0,4
	Новиков	0,4		0,4	0,4		0,4	+0,4
	Зимин	0,4		0,4	0,4		0,4	+0,4
	Давыдов	0,2	0,2	0,4	0,2	0,2	0,4