Вопрос 21-22 Условный экстремум Прямой метод и метод Лагранжа
Пусть на мн-ве 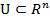 задана m+1 ф-ция
задана m+1 ф-ция 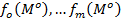 . Пусть Uo подмножество U, на котором
. Пусть Uo подмножество U, на котором 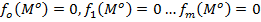 . (*)
. (*)
Ур-ние (*) – ур-ния свзяи.
ОПР: Т. хо 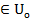 наз. точкой усл. экстремума на мн-ве U при условии выполнения ур-ний связи (*), если она явл. обычн. т. локаль. экстремума f(x) на мн-ве
наз. точкой усл. экстремума на мн-ве U при условии выполнения ур-ний связи (*), если она явл. обычн. т. локаль. экстремума f(x) на мн-ве 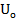 .
.
Прямой метод отыск. локальн. экстремума
Пусть требуется найти max или min ф-ции y=f(x1,x2,…xn) от перем x1,x2,…xn, которые связаны m соотношениями f1(x1,x2,…xn)=0 f2(x1,x2,…xn)=0 fm(x1,x2,…xn)=0. Разрешая эти соотнош. относит m переменных напр. x1,x2,…xn , мы выразим их через ост. n-m переменныe xn+1…xn. Подставл. эти соотн. в 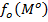 мы получим ф-цию от xm+1…xn перемен. и придём к отысканию обычн локального min и max этой ф-ции.
мы получим ф-цию от xm+1…xn перемен. и придём к отысканию обычн локального min и max этой ф-ции.
Метод Лагранжа: Пусть ф-ции f1(Mo), f2(Mo), fm(Mo) непрерыв. диф-ма в нек. окр. точки Mо из простр. 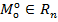 . Если т.
. Если т. 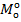 явл. точкой условн. лок. экстремума ф-ции f0(Mo ) относит. ур-ний связи, то в этой точке графдиент
явл. точкой условн. лок. экстремума ф-ции f0(Mo ) относит. ур-ний связи, то в этой точке графдиент 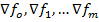 линейно зависимы, т.е. существуют числа
линейно зависимы, т.е. существуют числа 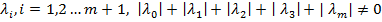 , что
, что 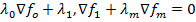
Следствие: в т. 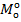 условного экстр ф-ции f0(Mo) относит ур-ний связи (*) градиент
условного экстр ф-ции f0(Mo) относит ур-ний связи (*) градиент 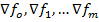 – линейно независимы, то найдутся числа
– линейно независимы, то найдутся числа 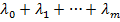 , что
, что 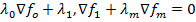 или координаты в форме:
или координаты в форме: 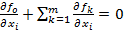 (1)
(1)
ОПР: Ф-ция F(Mo)=f(Mo)+ 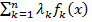 наз-ся формулой Лагранжа, а
наз-ся формулой Лагранжа, а 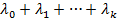 –множители лагранжа. Соотн. (1) означ, что точка Mo явл. критич. точкой ф-ции Лагранжа:
–множители лагранжа. Соотн. (1) означ, что точка Mo явл. критич. точкой ф-ции Лагранжа:
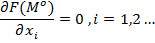
Вопрос 23 Числовые ряды, осн. определения, св-ва сходящихся рядов, критерий Коши сх-сти ряда, Признаки сх-ти числ. рядов с неотрицательными членами: Интегральный, сравнения, Даламбера, Коши, Теорема о перестановке членов ряда.
ОПР: Пара последовательностей 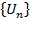 и
и 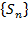 , где Sn=U1+U2+…+Un называется числ. рядом или бесконечной суммой и обознач.
, где Sn=U1+U2+…+Un называется числ. рядом или бесконечной суммой и обознач. 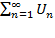 .
. 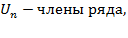 а эл-ты пос-ти Sn-частичные суммы ряда. Если сущ. конечный предел
а эл-ты пос-ти Sn-частичные суммы ряда. Если сущ. конечный предел 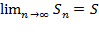 , то ряд – сходящийся и
, то ряд – сходящийся и 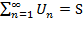 . Если пос-ть не стремится к 0, то ряд расходится.
. Если пос-ть не стремится к 0, то ряд расходится.
Простейшие свойства:
1. Ряды 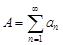 и
и 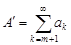 либо оба сходятся, либо оба расходятся. (Очевидно, т.к. критерий Коши даёт для обоих рядов одно и то же неравенство. При этом если ряды сходятся, то
либо оба сходятся, либо оба расходятся. (Очевидно, т.к. критерий Коши даёт для обоих рядов одно и то же неравенство. При этом если ряды сходятся, то 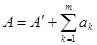 ) и
) и 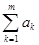 - n-ый остаток ряда.
- n-ый остаток ряда.
2. Пусть 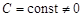 . Тогда
. Тогда 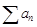 и
и 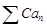 либо оба сходятся, либо оба расходятся. (Если обозначить
либо оба сходятся, либо оба расходятся. (Если обозначить 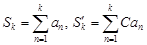 , то ясно, что
, то ясно, что 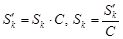 . Отсюда, если
. Отсюда, если 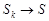 , то
, то 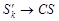 и т.п.).
и т.п.).
3. Если 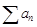 и
и 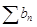 оба сходятся, то при
оба сходятся, то при 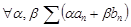 тоже сходится, причём
тоже сходится, причём 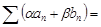
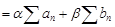 . (
. ( 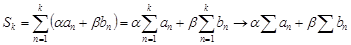 при
при 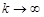 ).
).
Критерий Коши сх-сти ряда
Для того чтобы ряд сх-ся необх. и дост, чтобы для 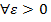 нашлось бы число nε, такое, что для всех n> nε и целых p.
нашлось бы число nε, такое, что для всех n> nε и целых p.
Док-во: 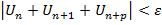 . Это утвержд. непосредств.=> из критерия Коши из последней сход-ти, поскольку
. Это утвержд. непосредств.=> из критерия Коши из последней сход-ти, поскольку 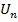 +
+ 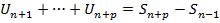
Необходимый и достаточный признак сходимости: Если 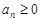 , то
, то 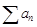 сходится тогда и только тогда, когда
сходится тогда и только тогда, когда 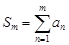 ограничена (сверху). То, что ряд сходится, равносильно тому, что существует конечный
ограничена (сверху). То, что ряд сходится, равносильно тому, что существует конечный 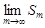 , а это, т.к.
, а это, т.к. 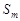 не убывает, равносильно ограниченности сверху
не убывает, равносильно ограниченности сверху 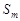 .
.
Ряды с положительными членами
Если 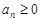 , то
, то 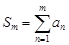 не убывает. (Действительно,
не убывает. (Действительно, 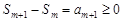 для
для 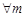 , т.е.
, т.е. 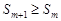 ).
).
Признак сравнения: Пусть даны 2 ряда 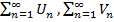 и
и 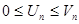 . Тогда из сходимости
. Тогда из сходимости 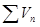 следует сходимость
следует сходимость 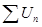 , из расходимости
, из расходимости 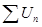 следует расходимость
следует расходимость 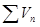 .
.
Док-во: а) Если ряд 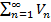 сх-ся, то он имеет конечн. сумму σ. Тогда
сх-ся, то он имеет конечн. сумму σ. Тогда 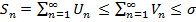 . Пос-ть частичн. сумм
. Пос-ть частичн. сумм 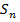 огранич. сверху, значит в силу леммы ряд
огранич. сверху, значит в силу леммы ряд 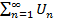 сх-ся.
сх-ся.
б) Если ряд 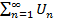 расх-ся, то и и ряд
расх-ся, то и и ряд 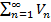 расх-ся, т.к. если это было не так и ряд
расх-ся, т.к. если это было не так и ряд 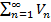 сх-ся, тов силу пункта а)
сх-ся, тов силу пункта а) 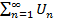 сх-ся.
сх-ся.
Признак Даламбера: Пусть 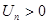 . Если при
. Если при 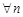 , начиная с некоторого, будет
, начиная с некоторого, будет 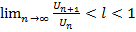 , то
, то 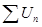 сходится, если же
сходится, если же 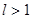 , то
, то 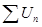 расходится.
расходится.
Док-во: Пусть l<1. Выберем число q так, что l<q<1. Т.к. 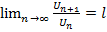 , то найд. номер no, что при n>no выполн. нер-во
, то найд. номер no, что при n>no выполн. нер-во 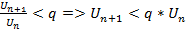 . Применим это нер-во последно для n=nо+1,nо+2…Получим
. Применим это нер-во последно для n=nо+1,nо+2…Получим 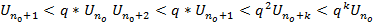 . Просуммируем эти нер-ва:
. Просуммируем эти нер-ва: 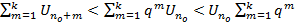 . Устремим
. Устремим 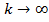 . Ряд
. Ряд 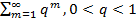 представл. собой сумму членов бескон. убыв. геометр. прогрессии. Значит в силу признака сравнения сх-ся и остаток ряда
представл. собой сумму членов бескон. убыв. геометр. прогрессии. Значит в силу признака сравнения сх-ся и остаток ряда 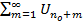 , а значит и сам ряд сх-ся.
, а значит и сам ряд сх-ся.
Радикальный признак Коши: Если для ряда 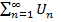
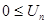 , =1,2… существует
, =1,2… существует 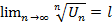 , то при l < 1 ряд сх-ся, при l > 1 рас-ся.
, то при l < 1 ряд сх-ся, при l > 1 рас-ся.
Док-во: Пусть l<1, тогда из существ 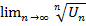 для : l<q<1 найдётся номер no: ∀ nо выполн. нер-во
для : l<q<1 найдётся номер no: ∀ nо выполн. нер-во 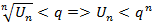 , n=nо+1,nо+2… Т.к. ряд
, n=nо+1,nо+2… Т.к. ряд 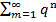 сх-ся, как бескон. убыв. геометр. прогрессия, то остаток ряда
сх-ся, как бескон. убыв. геометр. прогрессия, то остаток ряда 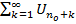 , а значит и сам ряд сх-ся.
, а значит и сам ряд сх-ся.
При 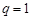 как в признаке Даламбера, так и в признаке Коши требуется дополнительное исследование.
как в признаке Даламбера, так и в признаке Коши требуется дополнительное исследование.
Интегральный признак Коши-Маклорена: Пусть 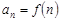 , причём
, причём 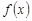 непрерывна на
непрерывна на 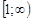 , монотонно убывает и
, монотонно убывает и 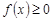 . Тогда
. Тогда 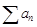 и
и 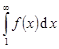 либо оба сходятся, либо оба расходятся.
либо оба сходятся, либо оба расходятся.
Док-во: Пусть k≤x≤k+1, k=1,2… Т.к. f(x) убывает, то f(k)≥f(x)≥f(k+1). Проинтегрируем от k до k+1:
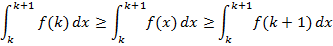
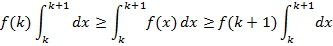
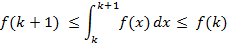
Проинтегрируем эти нерва от 1 до n: 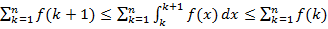
Замечание: 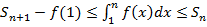
Если ряд сх-ся и его сумма равна S, то мнжво интегралов 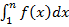 ограничено сверху, а в силу неотрицат
ограничено сверху, а в силу неотрицат 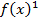
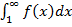 сх-ся.
сх-ся.
Теорема о перестановке членов ряда.
Пусть ряд 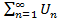 с неотр. членами сх-ся и имеет сумму S, тогда новый ряд, полученный в рез-те перестановки членов исходн. ряда так же сх-ся и имеет ту же сумму.
с неотр. членами сх-ся и имеет сумму S, тогда новый ряд, полученный в рез-те перестановки членов исходн. ряда так же сх-ся и имеет ту же сумму.
Док-во: Пусть ряд 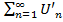 , а
, а 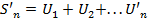 его частичн. сумма. Слагаемые этой частичн. суммы входят в исх. ряд под номерами k1, k2,…kn. Обозначим N – наиб. из этих номеров, тогда пусть SN –частич. сумма исх. ряда. Тогда
его частичн. сумма. Слагаемые этой частичн. суммы входят в исх. ряд под номерами k1, k2,…kn. Обозначим N – наиб. из этих номеров, тогда пусть SN –частич. сумма исх. ряда. Тогда 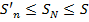 . Т.к n произвольна и S’n возрастает и огранич. сверху, то новый ряд сх-ся и его сумма
. Т.к n произвольна и S’n возрастает и огранич. сверху, то новый ряд сх-ся и его сумма 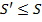 . Предполагаем аналог. рассуждения, взяв за исход. ряд не
. Предполагаем аналог. рассуждения, взяв за исход. ряд не 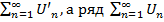 . тогда получим
. тогда получим 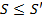 , значит
, значит 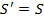 .
.
