Интегральный метод расчета пограничного слоя

Интегральный метод является универсальным – он применим как для расчета ламинарного, так и для расчета турбулентного пограничных слоев.

Этот метод основан на использовании уравнения Кармана, которое получается путем интегрирования по у дифференциальных уравнений пограничного слоя в частных производных, приведенных выше.

Уравнение Кармана в общем случае записывается следующим образом [2, 8]:

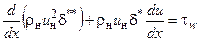
Для пограничного слоя на плоской поверхности (u_н = const , du_н/dx = 0, ρ_н = const) уравнение Кармана имеет вид

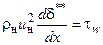(3.15)

Уравнение (3.15) содержит два неизвестных - d^** и t_w. Поэтому для его решения необходимо еще одно уравнение, которым является закон трения Ньютона

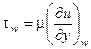(3.16)

Для определения (∂u/∂y)_w в уравнении (3.16) необходимо иметь выражение, описывающее изменение скорости в поперечных сечениях пограничного слоя, т.е. уравнение поля скоростей. Использование интегрального метода расчета возможно только для течений, поперечные поля которых обладают свойствами подобия и автомодельности. В случае пограничного слоя под подобием поперечных полей понимается совпадение безразмерных полей одноименных параметров в сходственных сечениях нескольких пограничных слоев, а под автомодельностью – независимость формы безразмерного поля некоторого параметра течения от продольной координаты х. В случае однофазных течений понятия подобия и автомодельности тождественны. Особенностью подобных и автомодельных течений является то, что для описания поперечного поля каждого параметра этих течений необходимо иметь только одно выражение, которое справедливо для любого сечения потока.

Подобие и автомодельность поперечных полей параметров жидкости имеют место в ламинарном и турбулентном пограничных слоях. В пределах переходного участка подобие и автомодельность отсутствуют.

Поле скоростей в ламинарном пограничном слое несжимаемой жидкости на плоской адиабатической поверхности хорошо аппроксимируется выражением [2, 8]

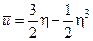(3.17)

в котором , .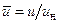

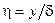В турбулентном пограничном слое вблизи обтекаемой поверхности число Рейнольдса, определенное по местным параметрам жидкости, может быть сколь угодно малым. Поэтому вблизи поверхности существует ламинарное течение. Эта часть пограничного слоя называется ламинарным подслоем. В нем скорость меняется по линейному закону

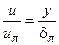
Здесь: u_л – скорость на границе ламинарного подслоя, d_л – его толщина.

Ламинарный подслой очень тонкий d_л/d ~ 0,01, но скорость на его границе относительно велика: u_л/u_н ~ 0,5.

Формулу для расчета поля скоростей в основной части турбулентного пограничного слоя можно получить, интегрируя выражение

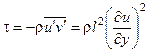, l = ky

В результате интегрирования получаем

.

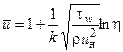Этой формулой пользоваться неудобно, так как необходимо знать t_w. Обычно для описания поля скоростей в турбулентном пограничном слое используется формула [2, 8]

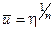, (3.18)

в которой n зависит от Re. При Re = 10⁶…10⁸ можно принять n = 7.

Используя уравнение Кармана (3.15), уравнение Ньютона (3.16), выражения (3.13) и (3.14) для d^* и d^**, формулы (3.17) и (3.18), описывающие изменение скорости в поперечных сечениях ламинарного и турбулентного пограничных слоев, можно получить формулы для расчета t_w, d, d^* и d^**. В случае течения несжимаемой жидкости вдоль плоской адиабатической поверхности эти формулы имеют вид:

для ламинарного пограничного слоя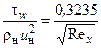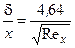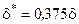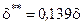

для турбулентного пограничного слоя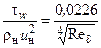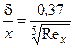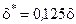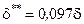

В приведенных формулах: 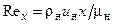, 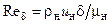. Значения коэффициентов в правых частях формул для турбулентного пограничного слоя соответствуют диапазону изменения числа Рейнольдса Re_x = 10⁶…10⁸, при котором показатель степени в формуле (3.18) равен 1/7.

Отрыв пограничного слоя

Рассмотрим обтекание крылового профиля дозвуковым потоком (рис. 3.4). Скорость жидкости, движущейся между невозмущенной линией тока и верхней поверхностью профиля, в соответствии с уравнением неразрывности на участке АВ будет возрастать, а на участке BD – падать. Согласно уравнению Бернулли давление на участке

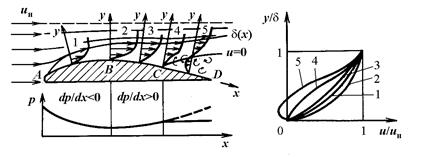АВ уменьшается (dp/dx < 0), а на участке BD – возрастает (dp/dx > 0). Можно показать, что при dp/dx ≠ 0 деформация неравномерных профилей скорости происходит всегда так, что скорость медленно движущихся слоев изменяется в большей степени, чем скорость быстродвижущихся. Поэтому в конфузорных течениях (на участке АВ) наполненность профиля скорости в пограничном слое увеличивается, а в диффузорных течениях (на участке BD) – уменьшается вдоль течения. В диффузорном течении кинетическая энергия жидкости расходуется на преодоление положительного градиента давления и на совершение работы трения, что приводит к уменьшению кинетической энергии пристенного слоя жидкости при движении от точки В к точке D. В точке С кинетическая энергия пристенного слоя жидкости и, следовательно, его скорость становится равной нулю. В этой точке (∂u/∂y)_w = 0. Жидкость из области повышенного давления (от точки D) устремляется к точке С и оттесняет пограничный слой от стенки – происходит отрыв пограничного слоя. В точке отрыва (∂u/∂y)_w = 0 и, следовательно, τ_w = μ(∂u/∂y)_w = 0. Из изложенного следует, что отрыв пограничного слоя происходит в потоках с положительным градиентом давления dp/dx>0. Это необходимое условие отрыва пограничного слоя. Достаточные условия отрыва пограничного слоя (критерии отрыва пограничного слоя) несжимаемой жидкости имеют вид [2, 8]:

- для ламинарного пограничного слоя

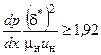или

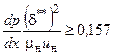
- для турбулентного пограничного слоя

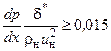или .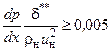

Так как профиль скорости в турбулентном пограничном слой более наполненный, то отрыв турбулентного пограничного слоя происходит при больших значениях dp/dx > 0.

Отрыв пограничного слоя можно предотвратить, уменьшая dp/dx>0 и толщину пограничного слоя, а также искусственно турбулизуя ламинарный пограничный слой перед точкой отрыва. Для уменьшения толщины пограничного слоя следует охлаждать поверхность, отсасывать или сдувать пограничный слой. При этом увеличивается поперечный градиент скорости ¶u/¶y, т.е. наполненность поперечного профиля скорости. Искусственная турбулизация ламинарного пограничного слоя достигается с помощью установки на поверхности турбулизирующего ребра.

3.2. Лабораторная работа "Теоретическое и экспериментальное исследование пограничного слоя на поверхности"

Цели работы - теоретическое и экспериментальное определение безразмерных полей скорости и толщин ламинарного и турбулентного пограничных слоев, сопоставление экспериментальных данных с результатами теоретического расчета, ознакомление с отрывом пограничного слоя и методами его предотвращения.