Объемный расход и средняя скорость в трубе

Объемный расход через поперечное сечение круглой трубы равен

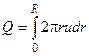
Подстановка в эту формулу выражения для скорости (1.3) с последующим интегрированием дает:

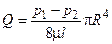(1.5)

Формула (1.5) выражает закон Пуазейля: при установившемся ламинарном движении вязкой несжимаемой жидкости в цилиндрической трубе круглого сечения объемный расход пропорционален перепаду давления на единицу длины трубы и четвертой степени ее радиуса.

Средняя скорость жидкости в поперечном сечении трубы с учетом (1.4) и (1.5) равна

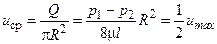
Следует отметить, что формула (1.5) позволяет экспериментально найти значение динамического коэффициента вязкости капельной жидкости. Этот метод определения коэффициента вязкости, называемый методом Пуазейля, рассматривается ниже.

Потери полного давления при течении вязкой несжимаемой

Жидкости в трубе

Любое течение вязкой жидкости сопровождается увеличением энтропии, связанным с необратимым преобразованием энергии жидкости в тепло, и, следовательно, с уменьшением полного давления жидкости. Получим формулу, которая позволяет рассчитывать уменьшение полного давления при течении несжимаемой жидкости в трубе.

Запишем для двух сечений трубы 1 и 2 уравнения неразрывности и Бернулли, полученные для элементарной струйки. Так как в элементарной струйке параметры жидкости принимаются постоянными поперек струйки, а в трубе скорость u переменна по радиусу трубы, то при использовании уравнений, полученных для элементарной струйки, для расчета течения в трубе в эти уравнения подставляется средняя скорость в сечениях трубы:

r₁u_ср1F₁ = r₂u_ср2F₂ (1.6)

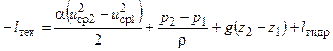(1.7)

В этих уравнениях: u_ср - средняя скорость в сечении трубы, F - площадь сечения трубы, z - положение сечения относительно нивелирной плоскости, для которой z = 0, l_тех - техническая работа, l_гидр- работа, затраченная жидкостью на преодоление гидравлических сопротивлений, a - коэффициент Кориолиса, учитывающий неравномерность поперечных полей скорости в трубе (для ламинарного течения a = 2 [8]).

При течении несжимаемой жидкости (r = const) в трубе постоянного сечения (F = const) из уравнения (1.6) следует u_cp2 = u_cp1, т.е скорость постоянна по длине трубы.

Если в трубопроводе между рассматриваемыми сечениями отсутствует насос, то l_тех= 0. При горизонтальном расположении трубы z₂ = z₁. В этом случае уравнение (1.7) упрощается:

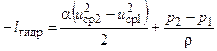(1.8)

Введя среднее по сечению трубы полное давление 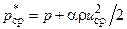, можно переписать формулу (1.8) в виде:

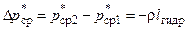(1.9)

Работа трения всегда положительна. Поэтому из уравнения (1.9) следует, что при течении вязкой жидкости в трубе полное давление уменьшается. Потери полного давления Dp^* складываются из потерь на трение на прямых участках канала постоянного сечения Dp_тр^* и местных потерь Dp_м^*, связанных с образованием и поддержанием вихревых зон при изменении площади канала, его повороте и т.п. Так как при течении несжимаемой жидкости средняя скорость не меняется по длине канала, то из формулы для давления торможения следует, что Dp_ср^* = Dp, т.е при течении несжимаемой жидкости в канале уменьшение полного давления на некотором участке канала численно равно уменьшению статического давления на этом участке (преодоление гидравлических сопротивлений происходит за счет уменьшения потенциальной энергии давления жидкости при неизменной ее кинетической энергии).

В гидравлике расчет изменения давления по длине круглой трубы на прямом ее участке проводится по формуле Дарси-Вейсбаха [8]

,

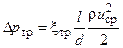в которой: x_тр- коэффициент трения, l - расстояние между рассматриваемыми сечениями, d - диаметр трубы, u_cp - средняя скорость жидкости в трубе.

Формула Дарси-Вейсбаха может быть использована для экспериментального определения коэффициента трения x_тр по определенным в эксперименте Dp_тр и u_cp при известных l и d.

Коэффициент трения зависит от режима течения. При ламинарном режиме течения он рассчитывается по формуле [8]

,

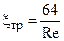в которой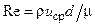

Факультативный материал