Непрерывность функции двух переменных.

Функция z = ƒ(х;у) (или ƒ(М)) называется непрерывной в точке М₀(х₀;у₀), если она:

а) определена в этой точке и некоторой ее окрестности,

б) имеет предел

в) этот предел равен 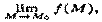значению функции z в точке Мо, т. е.

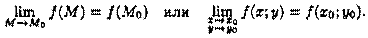
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции.

71. Производные и дифференциалы функции нескольких переменных.Пусть задана функция z = ƒ (х; у). Так как х и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Δх, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается ∆хz. Итак, Δхz=ƒ(х+Δх;у)-ƒ(х;у). Аналогично получаем частное приращение z по у: Δуz=ƒ(x;у+Δу)-ƒ(х;у). Полное приращение Δz функции z определяется равенством Δz = ƒ(х + Δх;у + Δу)- ƒ(х; у). Если существует предел 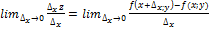, то он называется частной производной функции z = ƒ (х; у) в точке М(х;у) по переменной х и обозначается одним из символов: 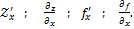Частные производные по х в точке 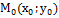обычно обозначают символами 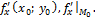Аналогично определяется и обозначается частная производная от z=ƒ(х;у) по переменной у: 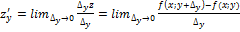. Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции ƒ(х;у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).

72. Применение дифференциала функции нескольких(двух) переменных к приближенным вычислениям.Полным дифференциалом функции нескольких переменных можно пользоваться для приближенных вычислений. Пусть дана дифференцируемая функция 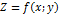.Её полное приращение выражается формулой 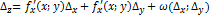. Здесь 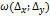стремиться к 0 быстрее чем, 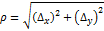. Поэтому при малых ρ, т.е. при малых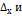 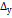, слагаемые 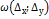можно пренебречь и написать: 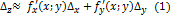, т.е. приращение функции можно приближенно заменить ее полным дифференциалом. 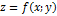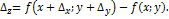Так как , то подставляем это выражение для 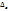в формулу (1.) получим: 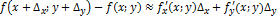, оттуда 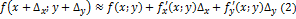.Формулой (2) можно пользоваться при приближении вычеслениях значений функции двух переменных в точке 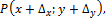близкой к точке P(x;y), если известны значения функции и ее части производных в самой точке P(x;y).

73. Частные производные первого порядка. Определение.Если существует конечный предел отношения частного приращения по x функции f(x,y,z) в точке M₀(x₀,y₀,z₀) к вызвавшему его приращению Δx при Δx 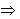0, то этот предел называется частной производной по х функции u=f(x,y,z) в точке М₀ и обозначается одним из символов: 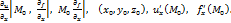По определению, 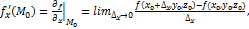Частные производные по у и по z определяются аналогично: 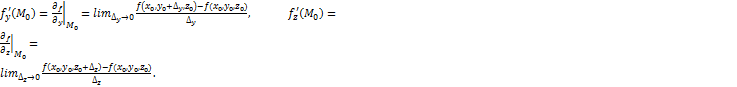Производные f'_x ; f'_y ; f'_z называются ещё и частными производными первого порядка функции f(x,y,z), или первыми частными производными. Так как частное приращение Δxf(M₀)получается лишь за счет приращения независимой переменной x при фиксированных значениях других независимых переменных, то частная производная f'_x(M₀) может рассматриваться как производная функции f(x₀,y₀,z₀) одного переменного x. Следовательно, чтобы найти производную по x, нужно все остальные независимые переменные считать постоянными и вычислять производную по x как от функции одного независимого переменного x. Аналогично вычисляются частные производные по другим независимым переменным. Если частные производные существуют в каждой точке области V, то они будут функциями тех же независимых переменных, что и сама функция.

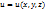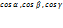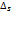74. Производная по направлению. Градиент. Пусть в некоторой области D задана функция и точка M(x,y,z). Проведем из точки M вектор , направляющие косинусы которого . На векторе , на расстоянии от его начала рассмотрим точку 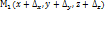, т.е. 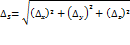. Будем предполагать, что функция u=u(x,y,z) и ее частные производные первого порядка непрерывны в области D. 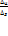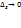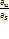Предел отношения при называется производной от функции u=u(x,y,z)в точке M(x,y,z)по направлению вектора и обозначается ,, т.е. 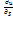. Для нахождения производной от функцииu=u(x,y,z) в заданной точке 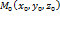по направлению вектора 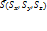используют 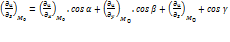формулу: где 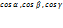– направляющие косинусы вектора 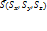, которые вычисляются по формулам: 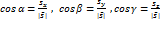. Пусть в каждой точке некоторой области D задана функцияu=u(x,y,z).Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функции u=u(x,y,z) и обозначается 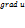или (читается «наблау»): . 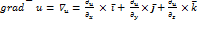При этом говорят, что в области D определено векторное поле градиентов. Для нахождения градиента функции u=u(x,y,z) в заданной точке 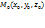используют формулу: 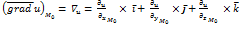. Свойства градиента1. Производная в данной точке по направлению вектора имеет наибольшее значение, если направление вектора совпадает с направлением градиента. Это наибольшее значение производной равно 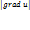. 2. Производная по направлению вектора, перпендикулярного к вектору grad u, равна нулю.

75. Экстремум функции нескольких переменных. Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной.Пусть функция z = f(x;у) определена в некоторой области D, точка N(x₀;y₀) Î D. Точка (х₀;у₀) называется точкой максимума функции z = f(x;y), если существует такая δ-окрестность точки (х₀;у₀), что для каждой точки (х;у), отличной от (х₀;у₀), из этой окрестности выполняется неравенство f(х;у)<f (x₀;y₀). Аналогично определяется точка минимумафункции: для всех точек (х;у), отличных от (x₀;y₀), из δ-ξкрестности точки (x₀;y₀) выполняется неравенство: f(x;y) > f(x₀;y₀). На рисунке 6: N₁- точка максимума, а N₂ - точка минимума функции z = f(x;y).Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называют ее экстремумами. Необходимые условия экстремума: если функция z=f(x,y) имеет в точке M₀(x₀,y₀) экстремум, то каждая частная производная первого порядка от z в этой точке или равна нулю 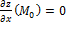, , 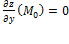или не существует. Точки, в которых частные производные 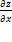и 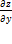функции z=f(x,y) равны нулю или не существуют, называются критическими точками этой функции. Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке (x₀;y₀) сравнивается с ее значениями в точках, достаточно близких к (x₀;y₀). В области D функция может иметь несколько экстремумов или не иметь ни одного.

76. Условный экстремум. Метод множителей Лагранжа. Функция z=f(x,y) 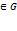имеет условный минимум(максимум) во внутренней точке M₀(x₀,y₀) 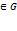, если для любых точек М(х,у) из некоторой окрестности О(М₀), удовлетворяющий уравнению связи ϕ(х,у)=0, выполняется условие ∆f(x₀,y₀)=f(x,y)-f(x₀,y₀)≥0, (∆f(x₀,y₀)≤0). В общем случае эта задача приводится к отысканию обычного экстремума Лагранжа L(x,y,λ)=f(x,y)=λϕ(x,y) с неизвестным множителем Лагранжа λ. Необходимое условие экстремума функции Лагранжа L(x,y,λ) представляет собой систему из трех уравнений с тремя неизвестными x,y,λ: 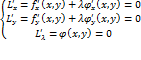. Достаточным условием для экстремума ф-ии Лагранжа заключается в следующем утверждении ∆>0, то ф-ия z=f(x,y) в точке M₀(x₀,y₀) имеет условный минимум, ∆<0- то условный максимум.

77. Числовые ряды. Основные понятия. Сходимость ряда. Числовым рядом называется выражение вида, 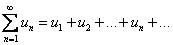где u₁ ,u₂,….,u_n,… – действительные или комплексные числа, называемые членами ряда, u_n - общим членом ряда. Ряд считается заданным, если известен общий член ряда u_n, выраженный как функция его номера n: u_n=f(n).Сумма первых n членов ряда называется n-й частичной суммой ряда и обозначается через S_n , т.е. S_n=u₁+u₂+…+u_n. Если существует конечный предел 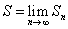последовательности частичных сумм ряда 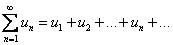, то этот предел называют суммой ряда и говорят, что ряд сходится.

78. Необходимый признак сходимости. Гармонический ряд. Теорема:Пусть числовой ряд u₁+u₂+…+u_n+…, (1) сходиться, а S-его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член u_n стремиться к 0. Этот признак яв-ся необходимым, но не достаточным признаком сходимости ряда, т.к. можно указать ряд, для которого выполняется равенство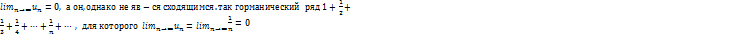

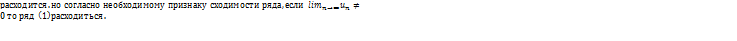На самом деле, если бы он сходился, то 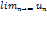равнялся бы 0. Таким образом, доказанная нами теорема иногда позволяет, не вычисляя суммы S_n, сделать заключение о расходимости того или иного ряда. Например, ряд 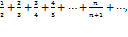расходиться так как 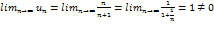. Гармонический ряд — сумма, составленная из бесконечного количества членов, обратных последовательным числам натурального ряда: 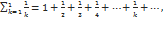Ряд назван гармоническим, так как складывается из «гармоник»: {\displaystyle k}-я гармоника, извлекаемая из скрипичной струны, — это основной тон, производимый струной длиной 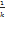{\displaystyle {\frac {1}{k}}} от длины исходной струны.