Производные основных элементарных функций.
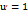
1)Степенные: 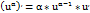
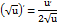
2)Показательные: 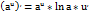
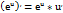
3)Логарифмические: 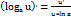
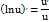
4)Тригонометрические: 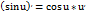
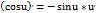
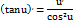
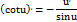
5)Обратно-тригонометрические: 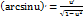
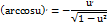
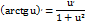
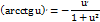
Производные высших порядков.
Очевидно, при дифференцировании элементарных функций снова получаются элементарные функции. В основном эти ф-ии имеют производную, тогда по отношению к исходной ф-ии эти производные будут второго порядка. Производной второго порядка называется производная от производной первого порядка. Аналогично дается определение производной n-го порядка. Производной n-го порядка называется производная от производной n-1 порядка.
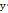 =y;
=y; 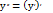 ;
; 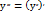 ;
; 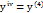
Дифференциал функции.
Главная линейная относительно ∆х часть приращения ф-ии, отличная от самого приращения на б.м.в. более высокого порядка, чем ∆х, называется дифференциалом ф-ии. Обозначается дифференциал dy. dy = 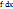 , где dx=∆х.
, где dx=∆х.
Понятие дифференциала функции.
Главная линейная относительно ∆х часть приращения ф-ии, отличная от самого приращения на б.м.в. более высокого порядка, чем ∆х, называется дифференциалом ф-ии. Обозначается дифференциал dy. Дифференциал dyназ-ют также дифференциалом 1-го порядка. Дифференциал независимой переменной равен приращению этой переменной: dx=∆x. Поэтому формулу можно записать так: dy = 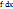 .Дифференциал ф-ии равен произведению производной этой ф-ии на дифференциал независимой переменной. Дифференциал функции составляет основную часть ее приращения.
.Дифференциал ф-ии равен произведению производной этой ф-ии на дифференциал независимой переменной. Дифференциал функции составляет основную часть ее приращения.
31:Основные теоремы о дифференциалах. 1)Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами: 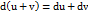 ,
, 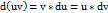
, 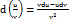 2)Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
2)Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Применение дифференциала к приближенным вычислениям.
Как уже известно, приращение  функции
функции 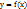 в точке X можно представить в виде
в точке X можно представить в виде 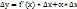 , где
, где 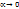 при
при 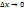 , или
, или 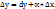 Отбрасывая бесконечно малую
Отбрасывая бесконечно малую 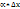 более высокого порядка, чем
более высокого порядка, чем  , получаем приближенное равенство
, получаем приближенное равенство 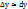 , причем это равенство тем точнее, чем меньше
, причем это равенство тем точнее, чем меньше 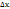 Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции. Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула
Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции. Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула 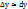 широко применяется в вычислительной практике.
широко применяется в вычислительной практике.
Дифференциалы высших порядков.
Пусть 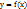 дифференцируемая функция, а ее аргумент x – независимая переменная. Тогда ее первый дифференциал
дифференцируемая функция, а ее аргумент x – независимая переменная. Тогда ее первый дифференциал 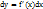 есть также функция x; можно найти дифференциал этой функции. Дифференциал от дифференциала функции
есть также функция x; можно найти дифференциал этой функции. Дифференциал от дифференциала функции 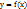 называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается
называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается  или
или 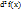
Дифференциалом порядка n, где n > 1, от функции z{\displaystyle ~z} в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1), то есть d^n z= d(d^n-1 z).
Таблица дифференциалов.
1. 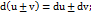
2. 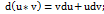
3. 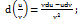
4. 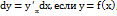
5. 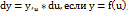
6. 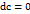 ;
;
7. 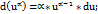
8. 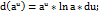
9. 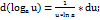
10. 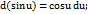
11. 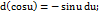
12. 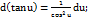
13. 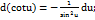
14. 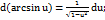
15. 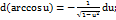
16. 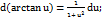
17. 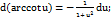
{\displaystyle ~d^{n}z=d(d^{n-135:Некоторые теоремы о дифференцируемых функциях.
Рассмотрим ряд теорем, имеющих большое теоретическое и прикладное значение.
Теорема Ролля: Если функция 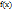 непрерывна на отрезке
непрерывна на отрезке 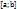 , дифференцируема на интервале
, дифференцируема на интервале 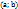 и на концах отрезка принимает одинаковые значения
и на концах отрезка принимает одинаковые значения 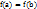 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 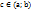 , в которой производная
, в которой производная 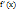 обращается в нуль, то есть
обращается в нуль, то есть 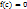 . Теорема Коши: Если функция
. Теорема Коши: Если функция 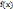 и
и 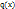 непрерывны на отрезке
непрерывны на отрезке 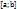 , дифференцируемы на интервале
, дифференцируемы на интервале 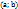 , причем
, причем 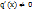 для
для 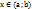 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 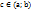 такая, что выполняется равенство
такая, что выполняется равенство 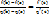 .
.
Теорема Лагранжа: Если функция 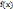 непрерывна на отрезке
непрерывна на отрезке 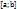 , дифференцируема на интервале
, дифференцируема на интервале 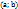 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 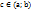 такая, что выполняется равенство
такая, что выполняется равенство 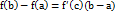 .
.
36: Правила Лопиталя. Теорема( Правило Лопиталя раскрытия неопределенностей вида ) . Пусть функции 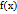 и
и 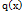 непрерывны и дифференцируемы в окрестности точки
непрерывны и дифференцируемы в окрестности точки 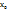 и обращаются в нуль в этой точке:
и обращаются в нуль в этой точке: 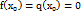 . Пусть
. Пусть 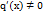 в окрестности точки
в окрестности точки 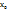 . Если существует предел
. Если существует предел 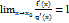 , то
, то 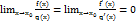
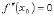 либо
либо 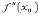 не существует. Теорема (Правило Лопиталя раскрытия неопределенностей вида
не существует. Теорема (Правило Лопиталя раскрытия неопределенностей вида  ). Пусть функция
). Пусть функция 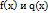 непрерывны и дифференцируемы в окрестности точки
непрерывны и дифференцируемы в окрестности точки  , в этой окрестности
, в этой окрестности 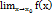 =
= 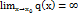 ,
, 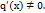 Если существует предел
Если существует предел 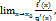 то
то 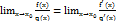 . Правило Лопиталя применяется для раскрытия неопределенностей вида и
. Правило Лопиталя применяется для раскрытия неопределенностей вида и 
 , которые называют основными.
, которые называют основными.
(Правило Лопиталя).
Пусть функции 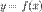 и
и 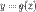 удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
1) эти функции дифференцируемы в окрестности точки 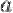 , кроме, может быть, самой точки
, кроме, может быть, самой точки  ;
;
2) 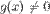 и
и 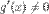 в этой окрестности;
в этой окрестности;
3) 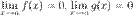 ;
;
4) 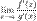 существует конечный или бесконечный.
существует конечный или бесконечный.
Тогда существует и 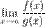 , причем
, причем 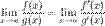
39. Первое и второе достаточные условия существования экстремума. Если непрерывная функция 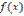 дифференцируема в некоторой δ-окрестности критической точки
дифференцируема в некоторой δ-окрестности критической точки 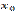 и при переходе через нее (слева направо) производная
и при переходе через нее (слева направо) производная 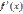 меняет знак с плюса на минус, то
меняет знак с плюса на минус, то 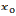 есть точка максимума; с минуса на плюс - то
есть точка максимума; с минуса на плюс - то 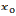 есть точка минимума. Доказательство: Рассмотрим -окрестность точки
есть точка минимума. Доказательство: Рассмотрим -окрестность точки 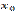 . Пусть
. Пусть 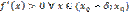 и
и 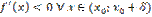 . Тогда функция
. Тогда функция 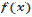 возрастает на интервале
возрастает на интервале 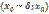 , а на интервале
, а на интервале 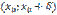 она убывает. Отсюда следует, что значение
она убывает. Отсюда следует, что значение 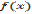 в точке
в точке 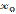 является наибольшим на интервале
является наибольшим на интервале 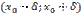 , т.е.
, т.е. 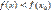 для всех
для всех 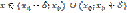 . Следовательно
. Следовательно 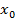 есть точка максимума. Второе достаточное условие:Если в точке
есть точка максимума. Второе достаточное условие:Если в точке 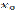 первая производная функции
первая производная функции 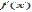 равна нулю (
равна нулю ( 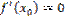 ), а вторая производная в точке
), а вторая производная в точке 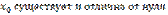 (
( 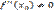 ), то при
), то при 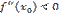 в точке
в точке 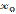 функция имеет максимум, а при
функция имеет максимум, а при 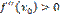 – минимум. Доказательство: Пусть
– минимум. Доказательство: Пусть 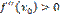 Т.к.
Т.к. 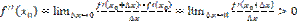 , то
, то 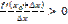 в достаточно малой окрестности точки
в достаточно малой окрестности точки 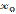 . Если
. Если 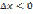 , то
, то 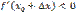 , если
, если 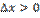 , то
, то 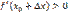 . Из этого следует, что при переходе через точку
. Из этого следует, что при переходе через точку 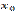 первая производная меняет знак с минуса на плюс. Следовательно
первая производная меняет знак с минуса на плюс. Следовательно 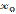 есть точка минимума.
есть точка минимума.
