Основные элементарные ф-ии и их графики. Тригонометрические ф-ии

Среди огромного числа функций в ходе развития математики была выделена небольшая совокупность сравнительно простых функций, особенно часто встречающихся в самых разнообразных приложениях математического анализа и поэтому подвергнутых наиболее подробному исследованию. Их называют основными элементарными функциями. К ним относят функции степенную, показательную и логарифмическую, тригонометрические и обратные тригонометрические функции.

Тригонометрические функции. К тригонометрическим относят следующие функции: , , . . Их графики представлены на рисунках

11. Основные элементарные функции и их графики. Обратные тригонометрические функции Среди огромного числа функций в ходе развития математики была выделена небольшая совокупность сравнительно простых функций, особенно часто встречающихся в самых разнообразных приложениях математического анализа и поэтому подвергнутых наиболее подробному исследованию. Их называют основными элементарными функциями.К ним относят функции степенную, показательную и логарифмическую, тригонометрические и обратные тригонометрические функции.К обратным тригонометрическим функциям относят : арксинус, арккосинус, арктангенс и арккотангенс/

1.Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ), имеющая область определения и множество значении .

2.Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ), имеющая область определения и множество значений .

3.Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ), имеющая область определения и множество значений

4.Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ), имеющая область определения и множество значений .

12. Числовая последовательность. Предел числовой последовательности Числовой последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров x₁,x₂,...x_n Числа x₁,x₂,...,x_n — называются элементами последовательности, символ x_n — общим элементом, а число n — его номером. Сокращенно последовательность обозначается символом {x_n}.Число а называется пределом последовательности{x_n}, если для любого ε > 0 найдется номер n₀ = n₀(ε) ∈ N такой, что для всех номеров n > n₀ выполняется неравенство |x_n — a| <ε Число b называется пределом последовательности {x_n}=x₁, x₂,..., x_n (lim {x_n} = b; n→∞) Последовательность {x_n}, имеющая конечный предел а, называется сходящейся.Последовательность, имеющая бесконечный предел или вообще не имеющая предела, называется расходящейся13. Предел функции. Определения. Основные теоремы о пределах Определение 1. Число А называется пределом функцииf(x) при , если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А. Определение 2. Число В называется пределом функции f(x) слева при , если для любой сходящейся к а последовательности аргументов функции , значения которых остаются меньше а , последовательность значений этой функции сходится к В. Обозначается: Определение 3. Число В называется пределом функции f(x) справа при , если для любой сходящейся к а последовательности аргументов функции , значения которых остаются больше а ( ), последовательность значений этой функции сходится к В. Обозначается: Определение 4. Предел функции f(x) в точке а существует, если существуют пределы слева и справа а и они равны между собой. Основные теоремы о пределах:1. Предел константы равен самой этой константе: 2. Постоянный множитель можно выносить за знак предела: 3. Предел суммы (разности) функций равен сумме (разности) пределов этих функций: 4. Предел произведения функций равен произведению пределов этих функций: 5. Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю:

14. Бесконечно большая функция (б.б.в.). Бесконечно малые функции (б.м.в.). Основные теоремы Функция f(x) называется бесконечно большой функцией в точке , если предел её в этой точке равен бесконечности. Функция f(x) называется бесконечно малой функцией в точке , если предел её в этой точке равен нулю. Основные теоремы:Теорема 1. Сумма конечного числа бесконечно малых функций (бесконечно больших функций одного знака) есть бесконечно малая функция(бесконечно большая функция). Теорема 2. Произведение конечного числа на бесконечно малую функцию (на б.б.в. кроме нуля) есть функция бесконечно малая (бесконечно большая). Теорема 3. Частное от деления бесконечно малой функции (бесконечно большой функции) на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая( бесконечно большая). Теорема 4.Если функция а(х)-бесконечно малая (а=0), то функция есть бесконечно большая функция и наоборот: если функция f(x)-бесконечно большая, то -бесконечно малая.

15. Первый замечательный предел. Второй замечательный предел Первый замечательный предел. Предел отношения синуса бесконечно малого аргумента к этому аргументу равен единице. Второй замечательный предел.Предел суммы единицы и бесконечно малой величины в степени ей обратной- бесконечно большой, равен числу е.

1) ; 2)

16. Эквивалентные бесконечно малые функции. Таблица эквивалентных величинЕсли то α и ß называются эквивалентными бесконечно малыми (при х→x₀); это обозначается так: α~ß Теорема 1: Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой. Теорема 2: Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них. Теорема 3: Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.

Таблица эквивалентных величин.

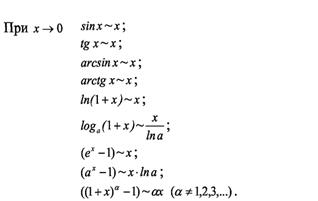17. Непрерывность функций в точке. Основные определения. Непрерывность функции на множестве Определение 1.Функция f(x) называется непрерывной в точкеa, если:1.функция f(x) определена в точке а и ее окрестности;2.существует конечный предел функции f(x) в точке a;3.этот предел равен значению функции в точке а, т.е. 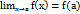Определение 2. 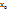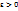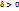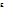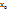Функция f(x) называется непрерывной в точке , если для любого заданного числа можно найти такое число (зависящее от и ), что для всех x, для которых 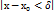, будет выполняться неравенство 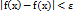Определение 3. Функция f(x) называется непрерывной в точке 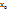, если бесконечно малому приращению аргумента 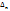соответствует бесконечно малое приращение функции 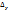, т. е. 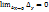. В некоторых случаях приходится пользоваться понятием односторонней непрерывности. Определение 4. Функция f(x), определенная в некоторой левой (правой) окрестности точки 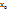, называется непрерывной слева (справа) в точке 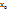, если существует предел слева (справа) функции y= f(x) и он равен 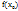. Определение 5. Функция f(x) , непрерывная во всех точках некоторого множества X, называется непрерывной на этом мно­жестве.

18. Точки разрыва функции I-го рода Определение. Точки разрыва функции I-го рода.Точка 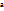, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно: Функция 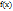определена в точке и ее окрестности;существует конечный предел функции 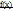в точке 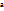;это предел равен значению функции в точке 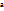, т.е. 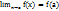называется точкой разрыва функции. Точка разрыва первого рода Определение Если в точке 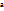существуют конечные пределы 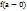и 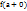, такие, что 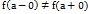, то точка 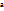называется точкой разрыва первого рода.

19. Точки разрыва функции II-го рода Определение Точка 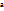, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

1. функция 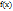определена в точке и ее окрестности;

2. существует конечный предел функции 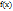в точке ;

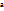3. это предел равен значению функции в точке 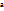, т.е.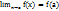

называется точкой разрыва функции.

Если хотя б один из пределов 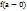или 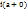не существует или равен бесконечности, то точка 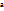называется точкой разрыва второго рода.

20. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций Основные теоремы о непрерывности функциях.Теорема 1. Сумма конечного числа непрерывных функций, определенных на некотором множестве Х, есть функция непрерывная. Теорема2. Произведение конечного числа непрерывных функций есть функция непрерывная. Теорема3. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, в которых делитель отличен от нуля. Теорема 4. Непрерывная функция от непрерывной функции есть функция непрерывная. Теорема 5. Если функция у=ƒ(х) непрерывна и строго монотонна на промежутке [a;b] оси Oх, то обратная функция у=φ(х) также непрерывна и монотонна на соответствующем отрезке [c;d] оси Оу Непрерывность элементарных функций Можно доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены. Как известно, элементарной называется такая функция, которую можно задать одной формулой, содержащей конечное число арифметических действий и суперпозиций (операции взятия функции от функции) основных элементарных функций. Поэтому из приведенных выше теорем вытекает: всякая элементарная функция непрерывна в каждой точке, в которой она определена.

21)Производная функции. Определение производной; её механический и геометрический смысл. Производной функции y=f(x) в точке 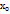называется конечный предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к 0. Функция, имеющая производную в точке 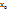, называется дифференцируемой в точке 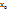. Операция нахождения производной ф-ииназ-ся дифференцированием. Скорость прямолинейного движения в материальной точке в момент времени t есть производная от пути s по времени t. Обобщая, можно сказать, что если ф-ия y=f(x) описывает какой-либо физический процесс, то производная y’ есть скорость протекания этого процесса. В этом состоит физический смысл производной. Значение производной ф-ции в точке 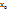равно угловому коэффициенту касательной к графику ф-ии в точке .

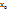22)Уравнение касательной и нормали к кривой.Как известно, из курса геометрии, уравнение прямой, проходящей через точку 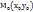с угловым коэффициентом k имеет вид y- 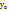=k(x- 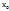), значит, уравнение касательной, проведенной к графику ф-ии y=f(x) в т. 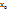можно записать в виде y – f( 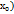= 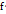( (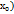x - 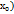. Как известно, угловые кафф. двух перпендикулярных прямых связан соотношением 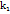= 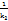, следовательно, уравнение нормали принимает вид y - f( 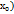= - 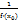(x - .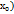

23)Связь между непрерывностью и дифференцируемостью функции. Если ф-ция дифференцируема, то она непрерывна. Обратное утверждение верно не всегда. Существуют функции, непрерывные в некоторой точке, но не имеющие в этой точке производной. Например: y = .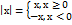

24)Производная суммы, разности, произведения и частного функции.Производная суммы двух ф-ий равна сумме производных этих ф-ий: 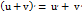. Производная разности двух ф-ий равна разности производных этих ф-ий: 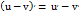. Производная произведения 2-х ф-ий равна произведению производной 1-го сомножителя на второй плюс произведение 1-го сомножителя на производную второго: 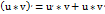. Производная частного 2-х ф-ий равна дроби, числитель которой есть разность произведений производного числителя на знаменатель дроби и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя: .

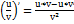25)Производная сложной и обратной функции. Рассмотрим сложную функцию y = y(u(x)). Теорема. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y'_u, u'_x), тогда сложная функция y = y(u(x)) дифференцируема и y'_x = y'_u u'_x. Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y). Теорема 5. Если обратная функция x = g(y) дифференцируема и g'(y) ≠ 0, то функция y=f(x) дифференцируема, и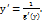

26)Дифференцирование неявных и параметрические заданных функций. Если независимая переменная x и функция y связаны уравнением вида F(x,y)=0 , которое не разрешено относительно y, то функция y называется неявной функцией переменной x.Всякую явно заданную функцию y=f(x) можно записать в неявном виде y-f(x)=0 . Обратно сделать не всегда возможно. Несмотря на то, что уравнение F(x,y)=0 не разрешимо относительно y, оказывается возможным найти производную от y по x. В этом случае необходимо продифференцировать обе части заданного уравнения, рассматривая функцию yкак функцию от x, а затем из полученного уравнения найти производную y’ . Предположим, что функциональная зависимость y от x не задана непосредственно y=f(x), а через промежуточную величину —t .Тогда формулы 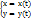задают параметрическое представление функции одной переменной. 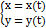Пусть функция задана параметрическими уравнениями где t – параметр. Тогда производная этой функции по переменной x равна отношению производных 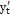и 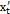по параметру t: 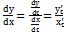Равнениями 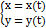где t – параметр. 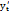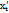Тогда производная этой функции по переменной x равна отношению производных и по параметру 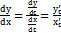t: