Условия задач, решаемых на лекциях (можно использовать при ответе на экзамене).

Площадь и статические моменты криволинейной трапеции (рис.1.11) определяются по формулам:

,

,

.

(1.12)

Формулы для осевых и центробежного моментов инерции:

,

,

.

(1.13)

Рис. 1.11 Плоская фигура, ограниченная кривой на

Пример 1.1 Найти осевые и центробежный моменты инерции прямоугольника относительно осей 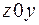(рис.1.9,а) и относительно центральных осей (рис.1.9,б)

Рис. 1.9 Прямоугольник

Пример 1.2 Определить полярный момент инерции круга, моменты инерции круга, полукруга, четверти круга относительно центральных осей ; (рис.1.10).

Рис.1.10 К примеру 1.2

Пример 1.3 Найдем координаты центра тяжести прямоугольного треугольника , (рис.1.13), осевые и центробежный моменты инерции.

Используем формулы (1.12), (1.13).

Рис.1.13Прямоугольный треугольник

Пример 1.4 Найдем координату центра тяжести полукруга (рис.1.14). Используем формулу (1.12) для .

Рис.1.14 Полукруг

Пример 1.5Определить центробежный момент инерции для четверти круга.

Рис. 1.15 К определению моментов инерции четверти круга

Пример 1.6 Прямоугольный равнобедренный треугольник со сторонами (рис.2). Вычислим главные моменты инерции и положение главных центральных осей инерции:

Рис.1.17 К определению главных центральных осей инерции

Пример 1.7Определим центр тяжести сложного сечения, состоящего из двух фигур (рис.1.18,а).

Рис. 1.18 Сложное сечение из двух фигур

Пример 3.1 Построить эпюру продольных сил .

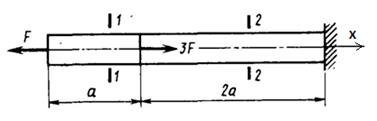
Рис.3.3

Пример 3.2 Построить эпюру продольных сил и продольных перемещений для стержня переменного сечения от действия собственного веса. Длина стержня 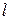. Поперечное сечение прямоугольник: высота сечения , ширина меняется по длине от 0 до . Объемный вес материала стержня .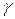

Рис.3.6

Пример 3.3 Для стержня, нагруженного как показано на рисунке, построить эпюру продольных перемещений w(x)

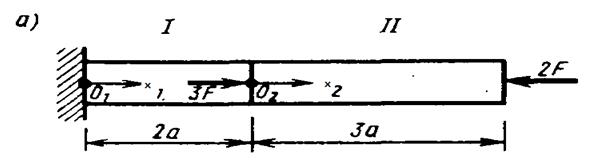
Пример 3.4Для стержня, нагруженного как показано на рис. 2.14 а, построить эпюру продольных сил и перемещений

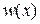
Рис.3.14 Статически неопределимая задача

Пример 5.1 Предположим, что рассматривая напряженное состояние в точке, мы выделили в ее окрестности элементарный параллелепипед и на его гранях обнаружили систему нормальных и касательных напряжений, обладающих тем свойством, что все компоненты оказались равными друг другу τ (рис. 5.3 а). Определим главные напряжения и установим, что же это за напряженное состояние.

Пример 5.2 Предположим, что рассматривая напряженное состояние в точке, мы выделили в ее окрестности элементарный параллелепипед и на его гранях обнаружили систему только равных касательных напряжений τ. Определим главные напряжения и установим, что же это за напряженное состояние.

Пример 7.1 Построить эпюры поперечных сил и изгибающих моментов для простой балки, нагруженной как показано на рис. 7.7 а.

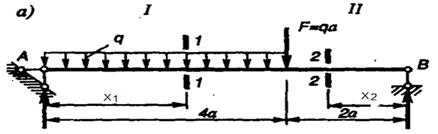
Рис.7.7

Каждый студент должен уметь самостоятельно составить выражения для Qи М и построить эпюры на участках для представленных схем загружения. (рис 7.9 )

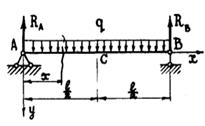Рис . 7.9

Влияние каждого вида нагрузок на характер эпюр поперечной силы и изгибающего момента показано на рис.7.11.Построить эпюры Qy, Mz, задавшись численными значениями параметров нагрузки и длин участков.

Рис. 7.11Законы изменения Q,Mв зависимости от нагружения

Пример 10.1 Шарнирно опертая балка перекрытия с пролетом 6м изготовляется из прокатного двутавра (рис. 9.2). 1) Подобрать его сечение, если расчетная равномерно распределенная нагрузка q=24 кН/м, расчетное сопротивление стали R=240 МПа.

2) Подобрать поперечное сечение двутавра для балки из примера 9.1 , используя расчеты по предельным нагрузкам.

\Пример 12.1 Построить эпюры , способом вырезания узлов и элементов.

Пример 12. 2. [1].Проверить прочность балки таврового сечения (рис.12.11), изготовленной из чугуна. Расчетное сопротивление на растяжение , расчетное сопротивление на сжатие .

Рис.12.11 Балка таврового сечения

Пример12.3 [1]. Для стальной балки указанного на рис.12.14, б сечения определить из условия прочности по методу предельных состояний наибольшую допустимую нагрузку . Построить эпюру для опасного сечения. В расчетах принять ; -коэффициент условий работы

Рис.12.14

Пример 13.1. Найдем перемещения для балки, загруженной нагрузкой, интенсивность которой изменяется по закону q=p(x/l).

Рис.13.3

Пример 13.2 Определить прогибы и внутренние усилия M и Q для балки (рис.13.4)

Рис.13.4

Пример 13.3 Определить перемещения используя локальной системы координат при наличии нескольких участков интегрирования.

Рис.13.5 Расчетная схема балки

Выражения для изгибающих моментов на участках имеют вид (см. лекцию №12 пример 12.1):

, , .

( )

Пример14.1 Выполнить расчет на жесткость балки, геометрическая схема которой с нормативной нагрузкой представлена на рис. 14.2

Рис.14.2

Пример 15.1 Стержень переменного сечения жестко заделан с двух концов и нагружен силой =40 кН (рис. 15.2,а). Построить эпюры N и .

Рис.15.2

Пример 15.2 Нагрузка в виде силы F=900 кН должна передаваться через жесткую балку на три железобетонных колонны с одинаковым поперечным сечением площадью A=400 см². При сборке системы было обнаружено, что средняя колонна изготовлена короче крайних на =0,15 см (рис.15.4). Определить усилия и напряжения в колоннах.

Рис.15.4

Пример15.3 Перекрытие цеха промышленного предприятия состоит из железобетонных плит, уложенных на кирпичные стены при температуре с зазором у одной из стен, равным (рис.15.5,а) . Температура в цехе может повышаться до 90⁰С. Возникнут ли дополнительные температурные напряжения в плитах перекрытия? Если эти напряжения возникнут, то чему они будут равны? Силами трения между плитой и ее опорной частью пренебрегаем. Толщина плиты h=20 см; коэффициент температурного расширения железобетона ; приведенный модуль упругости E=20 ГПа.

Пример15.4Для стержневой системы, изображенной на рис.15.6 ,а, определить силу при которой в наиболее напряженном стержне напряжения достигнут значения 240 МПа; м; см²; .

Рис. 15.6

Пример 16.1 Построить эпюры и для стержня ступенчато постоянного сечения, представленного на рис.16.9.

Рис. 16.9 Расчетная схема стержня

Пример 17.1 Стержень скручивается постоянным по длине моментом (рис.17.2). Дано: , , . Требуется подобрать диаметр стержня из условий прочности и жесткости.

Рис. 17.2 Кручение стержня