Графики и основные свойства элементарных функций

Основные свойства функций.

1) Область определения функции и область значений функции.

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции - это множество всех действительных значений y, которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

2) Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции.

Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.

6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

7) Периодическость функции.

Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Графики и основные свойства элементарных функций

График линейной функции

Линейная функция задается уравнением 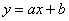. График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.

Пример 1

Построить график функции 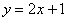. Найдем две точки. В качестве одной из точек выгодно выбрать ноль.

Если 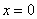, то

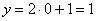
Берем еще какую-нибудь точку, например, 1.

Если 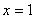, то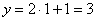

При оформлении заданий координаты точек обычно сводятся в таблицу:

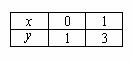
А сами значения рассчитываются устно или на черновике, калькуляторе.

Две точки найдены, выполним чертеж:

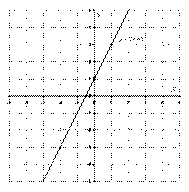
При оформлении чертежа всегда подписываем графики.

Не лишним будет вспомнить частные случаи линейной функции:

Обратите внимание, как я расположил подписи, подписи не должны допускать разночтений при изучении чертежа. В данном случае крайне нежелательно было поставить подпись рядом с точкой пересечения прямых 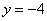, 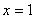или справа внизу между графиками.

1) Линейная функция вида 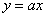( 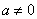) называется прямой пропорциональностью. Например, 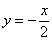. График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.

2) Уравнение вида 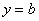задает прямую, параллельную оси 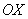, в частности, сама ось 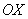задается уравнением 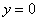. График функции строится сразу, без нахождения всяких точек. То есть, запись 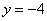следует понимать так: «игрек всегда равен –4, при любом значении икс».

3) Уравнение вида 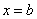задает прямую, параллельную оси 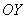, в частности, сама ось 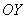задается уравнением 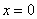. График функции также строится сразу. Запись 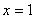следует понимать так: «икс всегда, при любом значении игрек, равен 1».

Некоторые спросят, ну зачем вспоминать 6 класс?! Так-то оно, может и так, только за годы практики я встретил добрый десяток студентов, которых ставила в тупик задача построения графика вроде 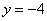или .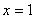

Построение прямой – самое распространенное действие при выполнении чертежей.

Прямая линия детально рассматривается в курсе аналитической геометрии, и желающие могут обратиться к статье Уравнение прямой на плоскости.

Кубическая парабола

Кубическая парабола задается функцией 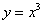. Вот знакомый со школы чертеж:

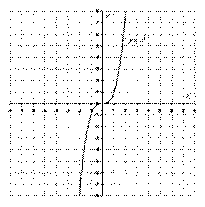
Перечислим основные свойства функции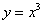

Область определения – любое действительное число: .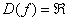

Область значений – любое действительное число: .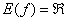

Функция 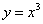является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием 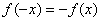. Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»:
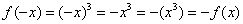, значит, функция 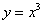является нечетной.

Функция 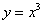не ограничена. На языке пределов функции это можно записать так: ,

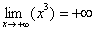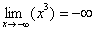
Кубическую параболу тоже удобнее строить с помощью алгоритма «челнока»:

Наверняка, вы заметили, в чем ещё проявляется нечетность функции. Если мы нашли, что 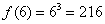, то при вычислении 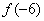уже не нужно ничего считать, автоматом записываем, что 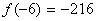. Эта особенность справедлива для любой нечетной функции.

А теперь поговорим о графиках функций-многочленов высоких степеней чуть более подробно. График функции 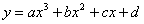( 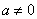) принципиально имеет следующий вид:

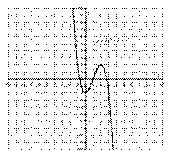
В этом примере коэффициент при старшей степени 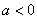, поэтому график развёрнут «наоборот». Принципиально такой же вид имеют графики функций-многочленов 5-й, 7-й, 9-й и других нечетных степеней. Чем выше степень, тем больше промежуточных «загибулин».

Функции-многочлены 4-й, 6-й и других четных степеней имеют график принципиально следующего вида:

Эти знания полезны при исследовании графиков функций.

График функции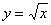

Он представляет собой одну из ветвей параболы. Выполним чертеж:

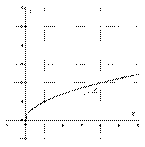
Основные свойства функции :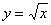

Область определения: .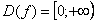

Область значений: .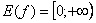

То есть, график функции полностью находится в первой координатной четверти.

Функция 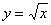не ограничена сверху. Или с помощью предела: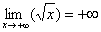

При построении простейших графиков с корнями также уместен поточечный способ построения, при этом выгодно подбирать такие значения «икс», чтобы корень извлекался нацело:

На самом деле хочется разобрать еще примеры с корнями, например, 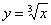, но они встречаются значительно реже. Сейчас я ориентируюсь на более распространенные случаи, и, как показывает практика, что-нибудь вроде 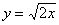приходиться строить значительно чаще. Однако унывать не нужно, в других статьях я рассмотрю самые разнообразные функции и их графики, корни в том числе.

График гиперболы

Опять же вспоминаем тривиальную «школьную» гиперболу .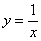

Выполним чертеж:

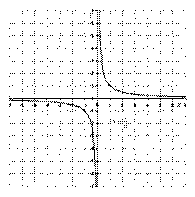
Основные свойства функции :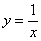

Область определения: .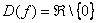

Область значений: .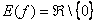

Запись 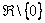обозначает: «любое действительное число, исключая ноль»

В точке 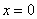функция терпит бесконечный разрыв. Или с помощью односторонних пределов: 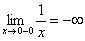, 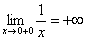. Немного поговорим об односторонних пределах. Запись 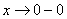обозначает, что мы бесконечно близко приближаемся по оси 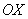к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси 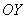. Именно этот факт и записывается пределом 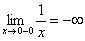. Аналогично, запись 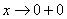обозначает, что мы бесконечно близко приближаемся по оси 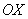к нулю справа. При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси 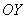. Или коротко: .

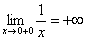Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.

В данном случае ось 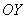является вертикальной асимптотой для графика гиперболы при .

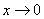Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.

Также односторонние пределы 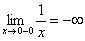, 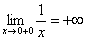говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.

Исследуем функцию на бесконечности: 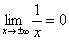, то есть, если мы начнем уходить по оси 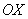влево (или вправо) на бесконечность, то «игреки» стройным шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси .

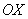Таким образом, ось 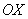является горизонтальной асимптотой для графика функции 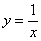, если «икс» стремится к плюс или минус бесконечности.

Функция 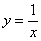является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .

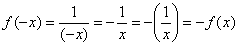График функции вида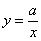(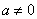) представляет собой две ветви гиперболы.

Если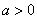, то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).

Если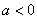, то гипербола расположена во второй и четвертой координатных четвертях.

Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.

Пример 3

Построить правую ветвь гиперболы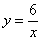

Используем поточечный метод построения, при этом, значения 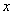выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

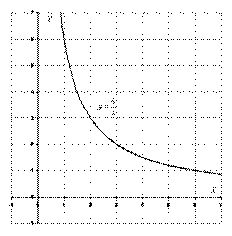
Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.

Детальную геометрическую информацию о рассмотренной линии можно найти в статьеГипербола и парабола.

График косинуса

Построим график функции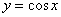

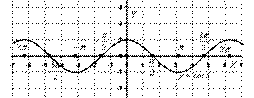
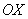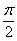График косинуса – это та же самая синусоида, сдвинутая вдоль осинавлево
(см. также Пример 8 урока о геометрических преобразованиях графиков).

Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.

Косинус – это функция четная, ее график симметричен относительно оси 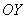, и справедлив следующий факт: 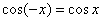. То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».

Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .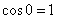

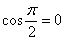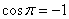Основные свойства функций.

1) Область определения функции и область значений функции.

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции - это множество всех действительных значений y, которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

2) Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции.

Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.

6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

7) Периодическость функции.

Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Графики и основные свойства элементарных функций

График линейной функции

Линейная функция задается уравнением 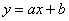. График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.

Пример 1

Построить график функции 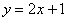. Найдем две точки. В качестве одной из точек выгодно выбрать ноль.

Если 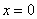, то

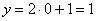
Берем еще какую-нибудь точку, например, 1.

Если 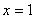, то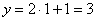

При оформлении заданий координаты точек обычно сводятся в таблицу:

А сами значения рассчитываются устно или на черновике, калькуляторе.

Две точки найдены, выполним чертеж:

При оформлении чертежа всегда подписываем графики.

Не лишним будет вспомнить частные случаи линейной функции:

Обратите внимание, как я расположил подписи, подписи не должны допускать разночтений при изучении чертежа. В данном случае крайне нежелательно было поставить подпись рядом с точкой пересечения прямых 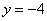, 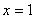или справа внизу между графиками.

1) Линейная функция вида 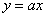( 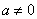) называется прямой пропорциональностью. Например, 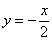. График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.

2) Уравнение вида 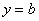задает прямую, параллельную оси 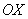, в частности, сама ось 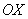задается уравнением 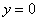. График функции строится сразу, без нахождения всяких точек. То есть, запись 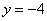следует понимать так: «игрек всегда равен –4, при любом значении икс».

3) Уравнение вида 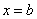задает прямую, параллельную оси 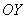, в частности, сама ось 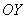задается уравнением 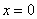. График функции также строится сразу. Запись 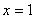следует понимать так: «икс всегда, при любом значении игрек, равен 1».

Некоторые спросят, ну зачем вспоминать 6 класс?! Так-то оно, может и так, только за годы практики я встретил добрый десяток студентов, которых ставила в тупик задача построения графика вроде 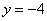или .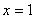

Построение прямой – самое распространенное действие при выполнении чертежей.

Прямая линия детально рассматривается в курсе аналитической геометрии, и желающие могут обратиться к статье Уравнение прямой на плоскости.