Средняя геометрическая величина

Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произве­дение индивидуальных величин, то следует применить геометрическую среднюю величину. Ее формула такова:

Средняя геометрическая: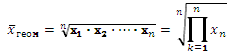

1) Основное применение геометрическая средняя находит при определении средних темпов роста, о чем будет сказано в теме «Ряды динамики».

Пусть, например, в результате инфляции за первый год цена товара возросла в 2 раза к предыдущему году, а за второй год еще в 3 раза к уровню предыдущего года. Ясно, что за два года цена выросла в 6 раз. Каков средний темп роста цены за год?

Арифме­тическая средняя здесь непригодна, ибо если за год цены возросли бы в 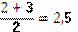раза, то за два года цена возросла бы в 2,5 х 2,5 = 6,25 раза, а не в 6 раз. Геометрическая средняя дает правильный ответ: 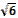= 2,45 раза.

2) Геометрическая средняя величина дает наиболее правильный по содержанию результат осреднения, если задача состоит в нахождении такого значения признака, который качественно был бы равно удален как от максимального, так и от минимального значения признака.

Например, если максимальный размер выиг­рыша в лотерее составляет миллион рублей, а минимальный — сто рублей, то какую величину выигрыша можно считать средней между миллионом и сотней?

Арифметическая средняя явно непригодна, она составляет 500 050 руб., а это, как и миллион, крупный, а никак не средний выигрыш; он качественно одноро­ден с максимальным и резко отличен от минимального.

Не дают верного ответа ни квадратическая средняя (707 107 руб.), ни кубическая (793 699 руб.), ни рассматриваемая далее гармоничес­кая средняя (199,98 руб.), слишком близкая к минимальному значению.

Только геометрическая средняя дает верный с точки прения экономики и логики ответ: 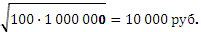Десять тысяч — не миллион, и не сотня! Это, действительно, нечто среднее между ними.

Средняя гармоническая

1. Средняя гармоническая невзвешенная.Эта форма средней имеет следующий вид:

Для иллюстрации области ее применения воспользуемся услов­ным примером. Пусть упаковкой и отправкой товаров занимают­ся два работника фирмы, специализирующейся на торговле по по­чте. Первый из них на обработку одного заказа затрачивает 8 мин., второй- 14 мин. Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?

На первый взгляд, ответ на этот вопрос заключается в осредне­нии индивидуальных значений затрат времени на 1 заказ, т.е. .

Проверимобоснованность такого подхода на примере одного часа работы. За этот час фактически первый работник обра­батывает 7,5 заказов (60 : 8), второй - 4,3 заказа (60 : 14). В сумме это составляет 11,8 заказа. Если же заменить индивидуальные зна­чения их предполагаемым средним значением, то общее число об­работанных обоими работниками заказов в данном случае умень­шится:

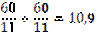заказов

Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени разделить на общее число обработанных за этот интервал двумя работниками заказов:

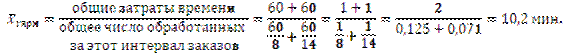
Проверим, если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за 1 час заказов не изменится:

заказов

Таким образом, средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения w_iдля единиц совокупности равны (рабочий день у сотрудников оди­наковый).

2. Средняя гармоническая взвешенная.Данная форма использует­ся, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель.

Рассмотрим расчет средней урожайно­сти, являющейся одним из основных показателей эффективности сельскохозяйственного производства (табл.).

Таблица - Валовой сбор и урожайность подсолнечника по центрально-черноземному району

(в хозяйствах всех категорий)*

Область	Валовой сбор, тыс. т	Урожайность, ц/га
Белгородская		16,1
Воронежская		9,5
Курская	0,5	4,8
Липецкая		10,9
Тамбовская		7,0

^{* Цифры приблизительные (90-е годы XX в.).}

Средняя урожайность любой сельскохозяйственной культуры по нескольким территориям, агрофирмам, фермерским хозяйствам и т. п. может быть определена только на основе следующего исход­ного соотношения:

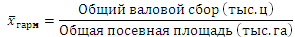
Общий валовой сбор мы получим простым суммированием ва­лового сбора по областям. Данные же о посевной площади отсут­ствуют, но их можно получить, разделив валовой сбор по каждой области на урожайность. С учетом этого определим искомую сред­нюю, предварительно переведя для сопоставимости тонны в цент­неры:

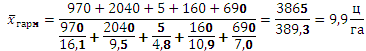
Таким образом, общая посевная площадь подсолнечника по Центрально-Черноземному району составляла 389,3 тыс. га, а сред­няя урожайность - 9,9 ц/га.

В данном примере расчет произведен по формуле средней гар­монической взвешенной:

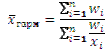, где .

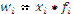Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса w за ряд временных интервалов.

ИЛИ (средняя гармоническая простая) ВАРИАНТ 2

Если по условиям задачи необходимо, чтобы неизменной оставалась при осреднении сумма величин, обратных индивидуальным значениям признака, то средняя величина является гармонической средней.

Формула гармонической средней величины такова:

Например, автомобиль с грузом от предприятия до склада ехал со скоростью 40км/ч, а обратно порожняком — со скоростью 60км/ч. Какова средняя скорость автомобиля за обе поездки? Пусть расстояние перевозки составляло S км. Никакой роли при расчете средней скорости величина S не играет. При замене индивиду­альных значений скорости х₁ = 60 и х₂ = 40 на среднюю величину необходимо, чтобы неизменной величиной осталось время, зат­раченное на обе поездки, иначе средняя скорость может оказаться любой — от скорости черепахи до скорости света. Время поездок есть s/x₁+s/x₂. Итак, s/x + s/x= s/x₁ + s/x₂. Сокра­тив все члены равенства на s, получим 1/х + 1/х = 1/х₁ + 1//x₂. т.е. выполняется условие гармонической средней. Подставляя х₁ и х₂, получаем:

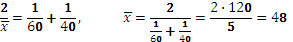км/ч.

Арифметическая средняя 50 км в час неверна, так как приво­дит к другому времени движения, чем на самом деле. Если расстояние равно 96 км, то реальное время движения составит:

То же время дает гармоническая средняя 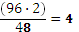.