Аппроксимация законов движения с ускорением

Разгон с постоянным ускорением – установившееся движение (с постоянной скоростью) – торможение с постоянным ускорением. Это – движение с четырьмя «мягкими» ударами (рис. П4).

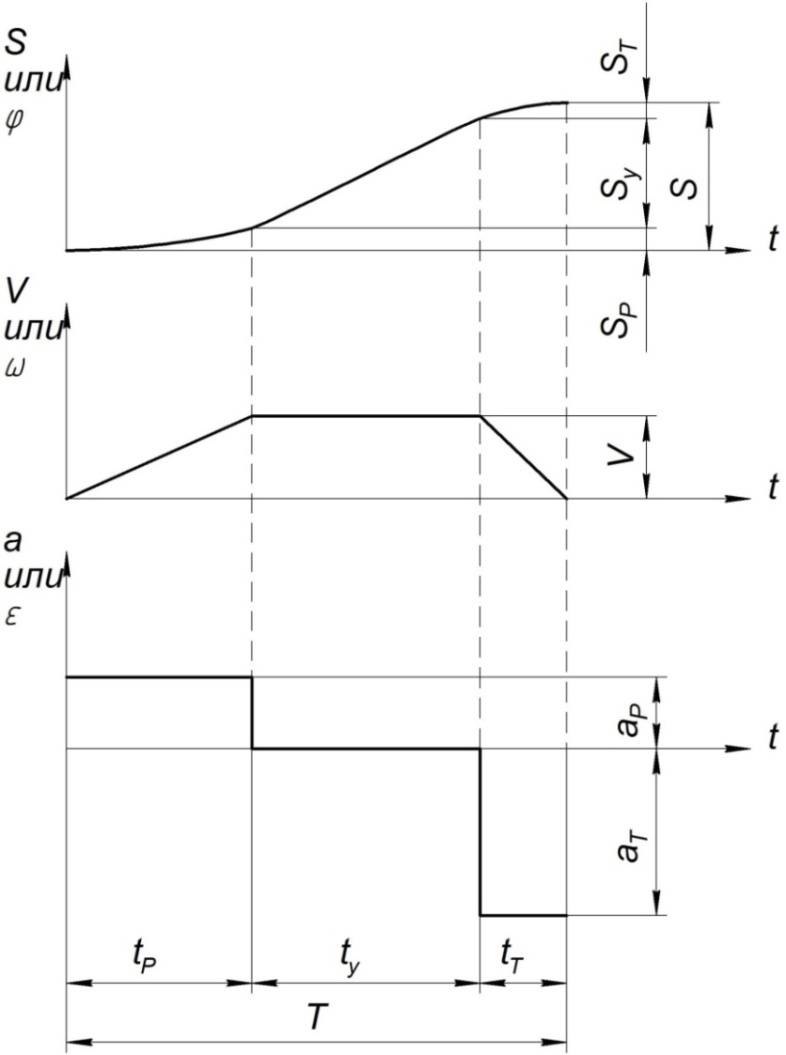
Рис. П4. Законы изменения параметров движения при a(t) = const

Если заданы перемещение S, время разгона t_р, время установившегося движения t_у, время торможения t_т, то:

перемещения при разгоне, движении с постоянной скоростью, торможении

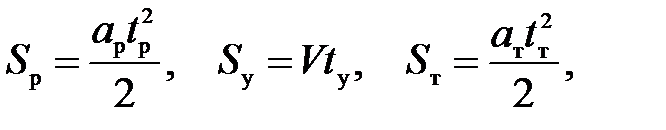(П.13)

максимальная скорость

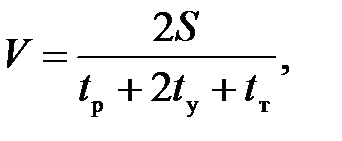(П.14)

ускорения при разгоне и торможении

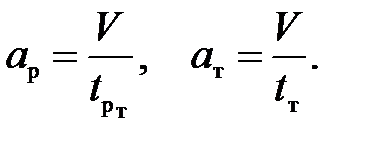(П.15)

Если заданы перемещение S, ускорение a_р = a_т = a и время T перемещения на величину хода, то максимальная скорость:

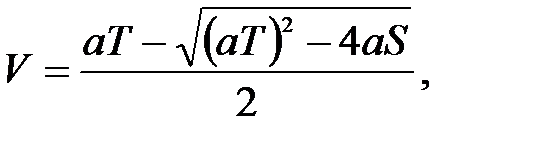(П.16)

а если заданы S, V и a, то время перемещения

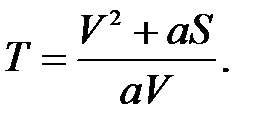(П.17)

Разгон – установившееся движение – торможение с ускорениями, изменяющимися по закону a(t) = a×sinwt. Это – безударное управляемое движение (рис. П5).

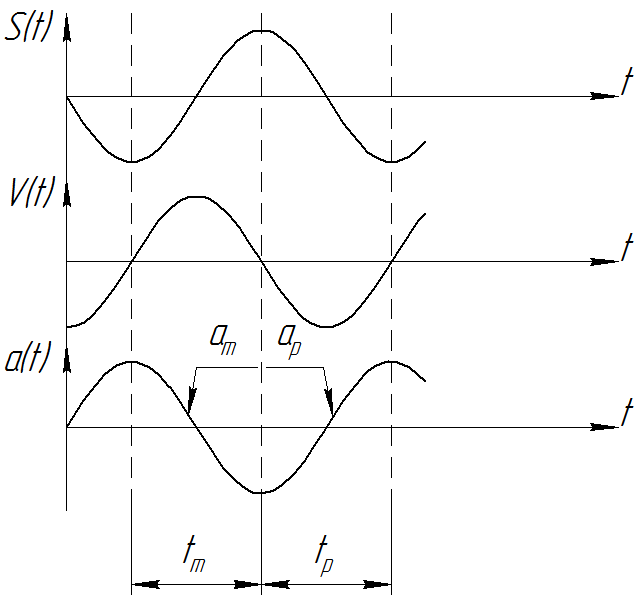
Рис. П5. Законы изменения параметров движения при a(t) = a×sinwt

текущее ускорение звена

на участке разгона

a(t) = a_рsinw₁t, (П.18)

на участке торможения

a(t) = a_тsinw₂t, (П.19)

где w₁, w₂ – круговые частоты на участках разгона и торможения;

w₁ = 2pf₁ = p/t_р, w₂ = 2pf₂ = p/t_т.

текущая скорость звена

на участке разгона

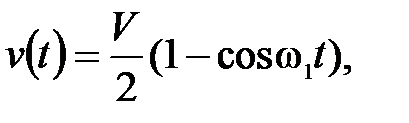(П.20)

на участке торможения

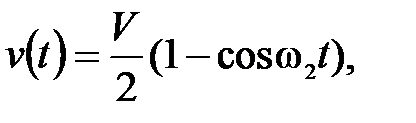(П.21)

на участке установившегося движения

v(t) = V.

текущее перемещение звена S(t) = ò v(t)dt

на участке разгона

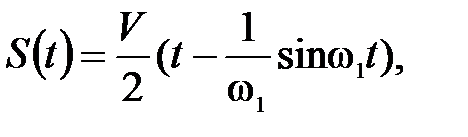(П.22)

на участке торможения

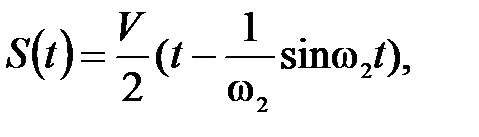(П.23)

на участке установившегося движения S(t) = Vt.

Если заданы перемещение S, время движения T, время разгона t_р и время торможения t_т, то

максимальная скорость

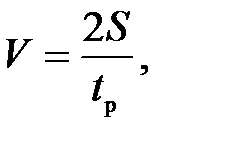(П.24)

максимальное ускорение на участке разгона

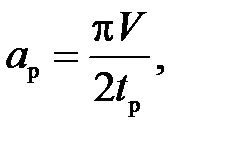(П.25)

максимальное ускорение на участке торможения

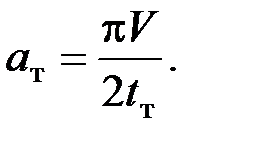(П.26)

Движение точки звена по окружности

Перемещение точки по дуге радиуса R

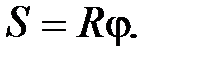(П.27)

где j - угол дуги.

Угловая скорость

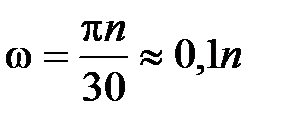(рад/с, 1/с), (П.28)

где n - частота вращения или скорость вращения (об/мин, 1/мин).

Окружная скорость

V = wR (П.29)

Ускорение точки М (рис. П6)

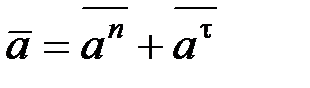(П.30)

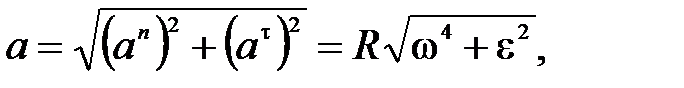
где aⁿ = w²R – нормальное ускорение, a^t = eR – тангенциальное ускорение.

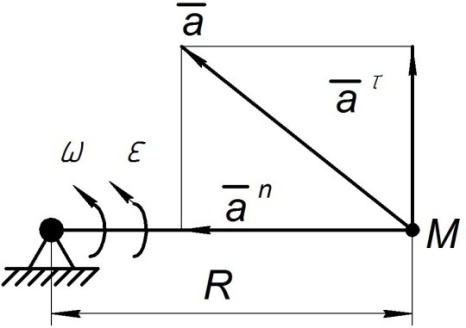
Рис. П6. Ускорение точки звена при вращении

Скорость и ускорение точки звена при наличии относительного движения (рис. П7)

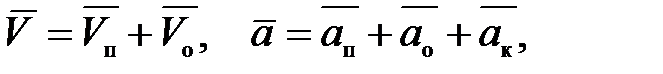(П.31)

где 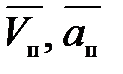- скорость и ускорение точки в переносном движении,

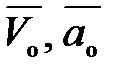- скорость и ускорение точки в относительном движении,

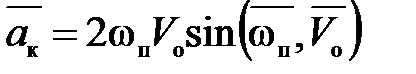- ускорение Кориолиса.

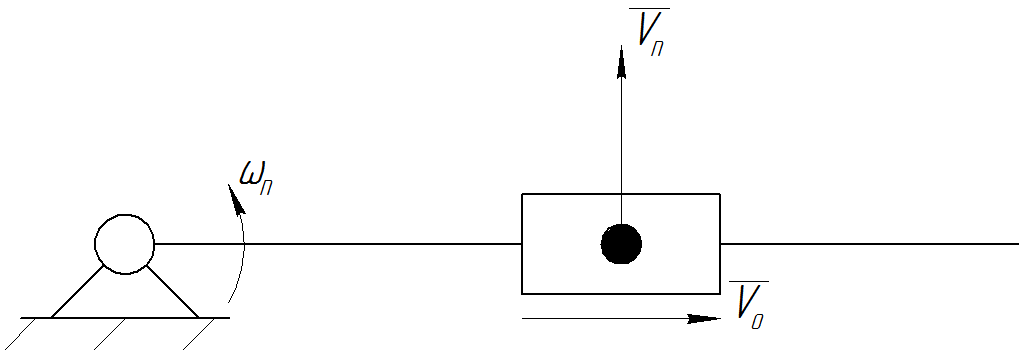
Рис. П7. Переносное и относительное движение точки звена

СИЛА, МОМЕНТ СИЛЫ

Сложение сил

Равнодействующая сил 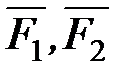(рис. П8), приложенных в одной точке

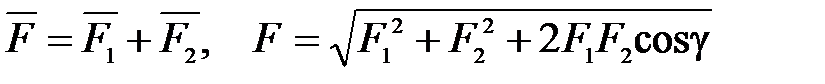(П.32)

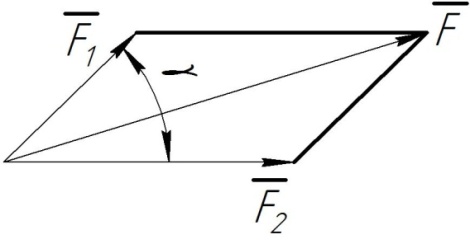
Рис. П8. Сложение сил, приложенных в одной точке

Равнодействующая параллельных сил 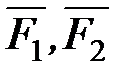(рис. П9)

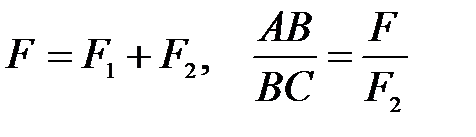(П.33)

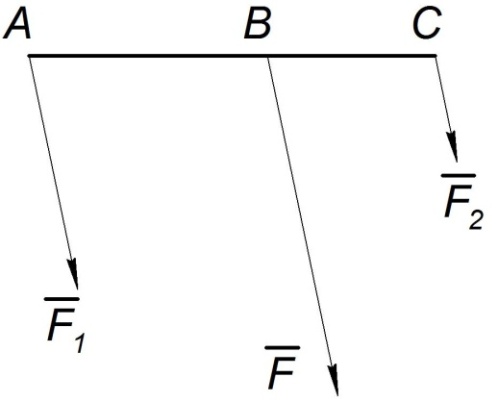
Рис. П9. Сложение параллельных сил

Момент силы F относительно оси Z (рис. П10)

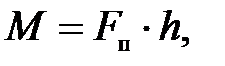(П.34)

где F_п – проекция силы 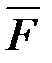на плоскость П, перпендикулярную оси Z,

h – плечо силы.

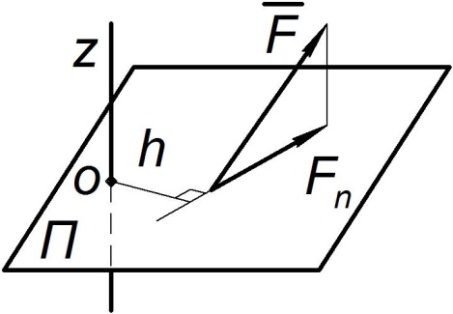
Рис. П10. Момент силы относительно оси

Момент пары сил (рис. П11)

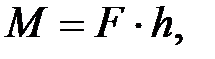(П.35)

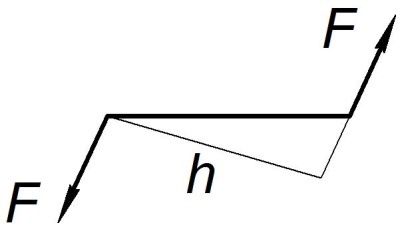
Рис. П11. Момент пары сил

Параллельное смещение силы из точки А в точку В (рис. П12)

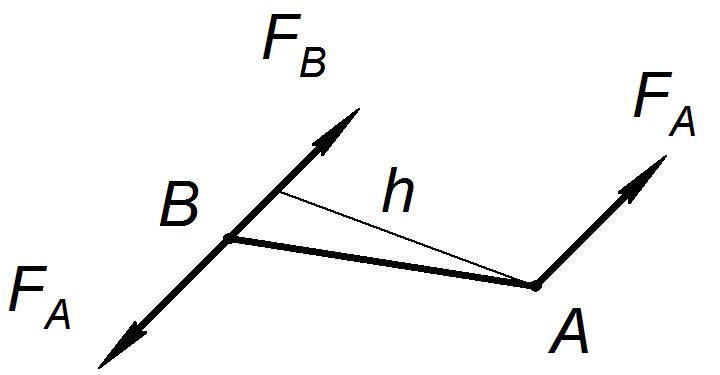
Рис. П12. Параллельное смещение силы

Эквивалентом силы F_A является сила F_B = F_A и пара сил F_A с плечом h.

Система уравнений равновесия звена

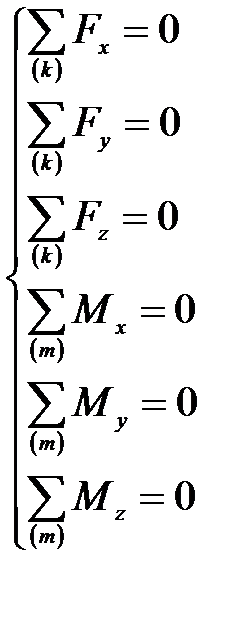, (П.36)

где F_x, F_y, F_z – проекции силы на оси координат;

M_x, M_y, M_z – моменты силы и моменты пары сил относительно осей координат;

k – число сил, действующих на звено;

m – число моментов сил и пар сил, действующих на звено.

Сила тяжести

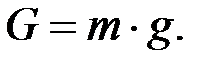(П.37)

Тело массой 1 кг имеет вес G = 1×9,81 = 9,81 Н = 1 кгс.

Сила трения скольжения

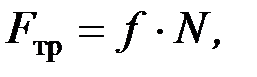(П.38)

где f – коэффициент трения скольжения, который зависит от скорости скольжения V и изменяется от f_max = f_п до f_min (рис. П13);

N – нормальное давление;

f_п – коэффициент трения покоя.

При наличии смазки коэффициенты трения движения и покоя:

в паре сталь-сталь f = 0,1…0,2; f_п = 0,2…0,3,

в паре сталь-бронза f = 0,1…0,15; f_п = 0,15…0,2.

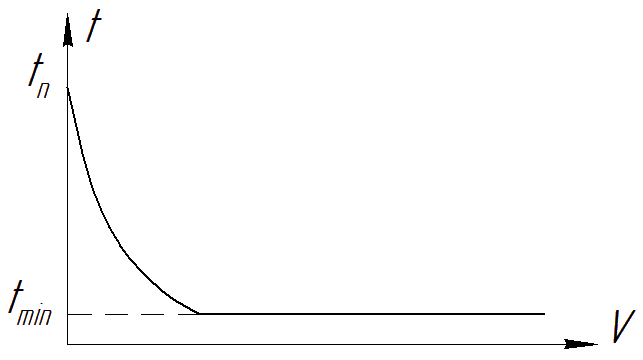
Рис. П13. Коэффициент трения скольжения

Момент трения в подшипнике скольжения

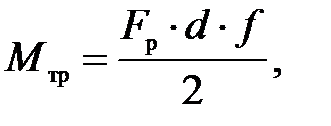(П.39)

где F_р – радиальная нагрузка на подшипник;

d – диаметр подшипника.

Момент сопротивления при качении

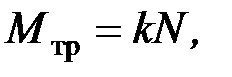(П.40)

где k – коэффициент трения качения (плечо пары трения).

Для катка на плоской пластине

k » 1×10^-5 м, если каток и пластина сделаны из закаленной стали,

k » 5×10^-5 м, если каток и пластина сделаны из мягкой стали или чугуна.

Приведенная сила трения, которая действует на объект, движущийся на колесах (рис. П14)

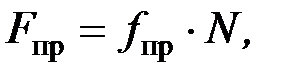(П.41)

где f_пр – приведенный коэффициент трения, который зависит от конструкции и качества узла колеса и от дороги.

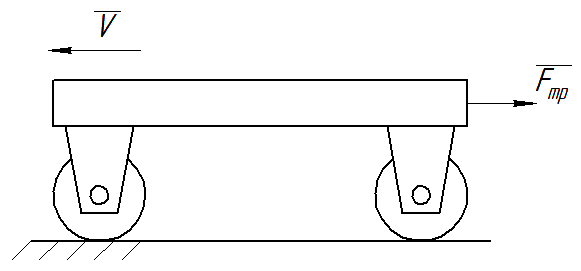
Рис. П14. Объект на колесах

Момент трения в подшипнике качения

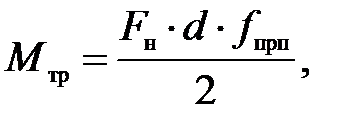(П.42)

где 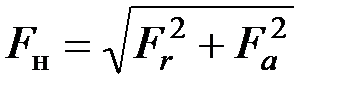- нагрузка на подшипник;

F_r и F_a – радиальная и осевая нагрузки на подшипник;

d – внутренний диаметр подшипника;

f_прп – приведенный коэффициент трения в подшипнике, который учитывает все источники трения в подшипнике, f_прп » const.

Для шариковых и роликовых подшипников f_прп = 0,002…0,01.

Сила инерции в поступательном движении

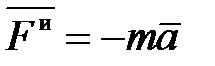. (П.42)

Момент сил инерции при вращении

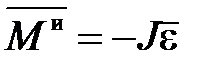. (П.43)

Движущая сила при поступательном движении

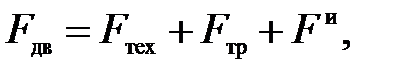(П.44)

где F_тех – сила технологического сопротивления;

F_тр – сила трения;

F^и – сила инерции, F^и = const при использовании принципа кинетостатики.

Движущий момент при вращении

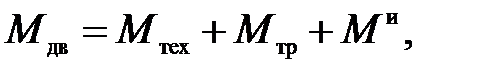(П.45)

где М_тех – момент технологического сопротивления;

М_тр – момент сил трения;

М^и – момент сил инерции.

Пример

Ползун П движется с ускорением и преодолевает технологическое сопротивление (рис. П15).

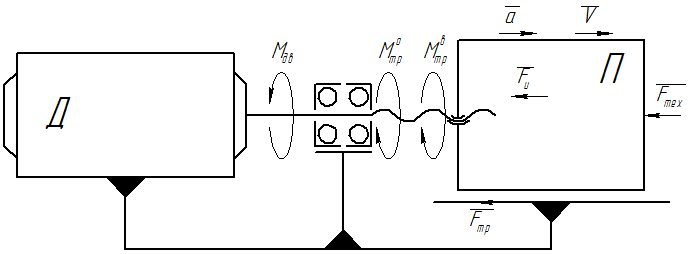
Рис. П15. Движущий момент при перемещении ползуна

Движущий момент на валу двигателя Д

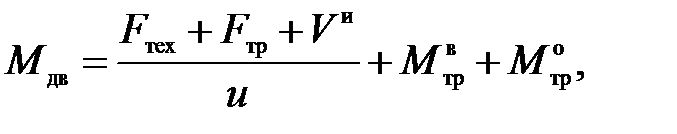
где F_тех – технологическое усилие, действующее на ползун;

F_тр – сила трения в опоре ползуна;

F^и – сила инерции ползуна;

U – передаточное число винтовой передачи;

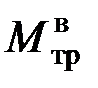– момент трения в винтовой передаче;

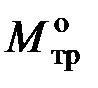– момент трения в опоре винта.

Гироскопический момент (рис. П16)

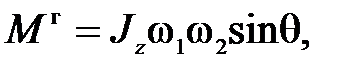(П.46)

где J_z – момент инерции звена, вращающегося вокруг оси своей симметрии;

w₁ – скорость вращения звена;

w₂ – скорость вращения оси симметрии;

q – угол между векторам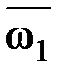и и .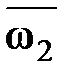

Уравнение движения при поступательном движении звена

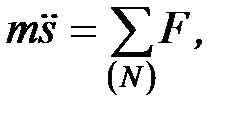(П.47)

где m – масса звена;

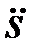– ускорение центра масс;

F – внешняя сила, действующая на звено;

N – число внешних сил.

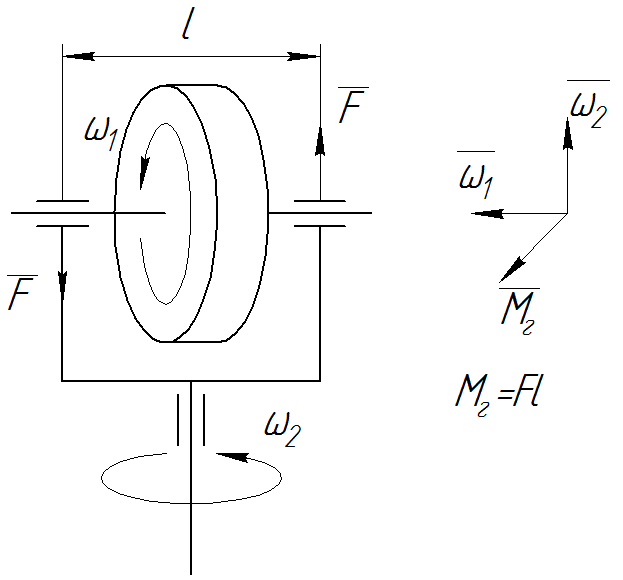
Рис. П16. Гироскопический момент

Уравнение движения при вращении звена вокруг оси

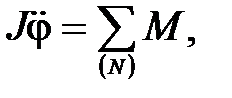(П.48)

где J – момент инерции звена;

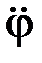– угловое ускорение звена;

М – момент внешней силы, действующей на звено;

N – число моментов.

Кинетическая энергия звена, движущегося поступательно

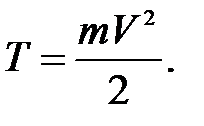(П.49)

Кинетическая энергия вращающегося звена

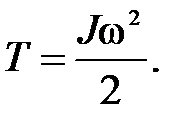(П.50)

Потенциальная энергия (работа) при перемещении звена в поле сил тяжести

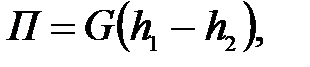(П.51)

где h₁ и h₂ - начальное и конечное положения звена по высоте подъема.

Потенциальная энергия сжатой (или растянутой) пружины

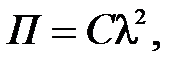(П.52)

где С - жесткость пружины;

l - деформация пружины.

Закон сохранения механической энергии

Т + П = const (П.53)

Уравнение Лагранжа 2-го рода

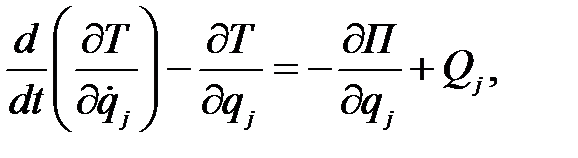(П.54)

где Т и П – кинетическая и потенциальная энергия системы;

q_j – обобщенная координата, j = 1, 2, …;

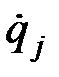– обобщенная скорость;

Q_j – обобщенная сила.

Пример

Блок (рис. П17) весом G₀ радиуса r с массой, распределенной по ободу, приводится во вращение канатом, несущим грузы G₁ и G₂ > G₁. Найдем ускорение e блока.

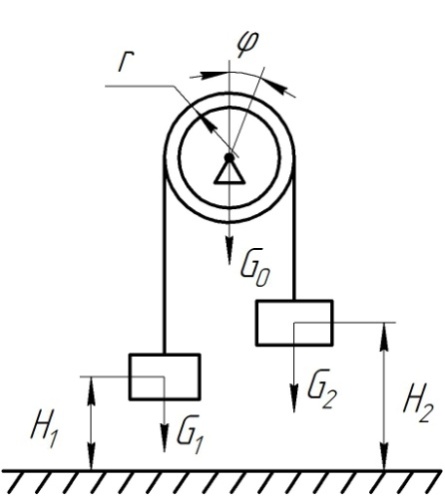
Рис. П17. Блок с грузами

Выберем в качестве обобщенной координаты угол j. Тогда

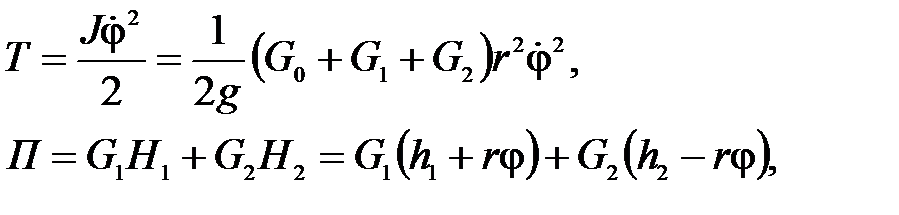
где h₁, h₂ – начальные высоты грузов над горизонтальной плоскостью.

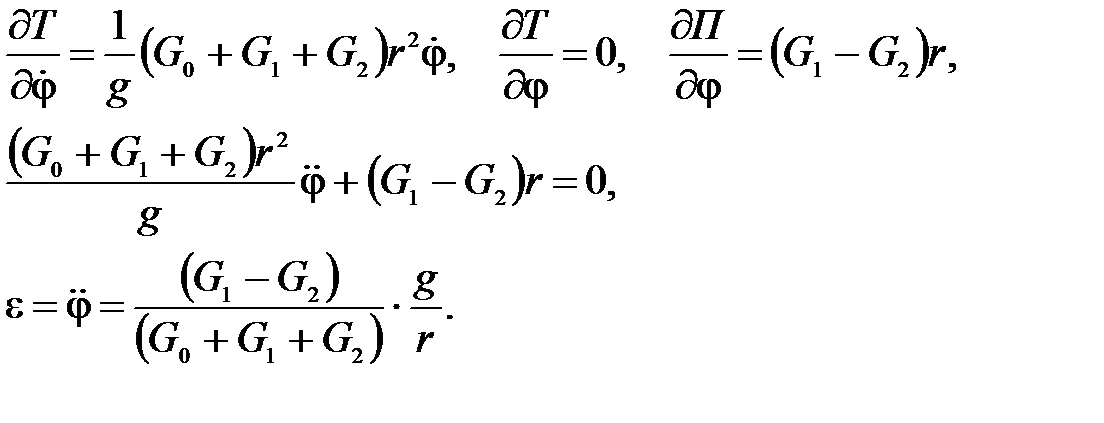
Мощность при поступательном движении

Р = FV (П.55)

Мощность при вращении

Р = Мw (П.56)

Мощность двигателя

Р_дв = Р_из + Р_пот, (П.57)

где Р_из - мощность на исполнительном звене механизма;

Р_пот - мощность потерь в передаче движения от двигателя к исполнительному звену.

Р_дв = Р_из/h (П.58)

где h - КПД передач движения, h = f(Р_из).

Средняя мощность на участке траектории движения с координатой S₁ £ s £ S₂

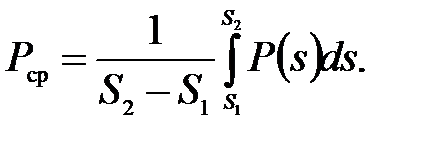(П.59)

ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ

Упрощенная структура привода представлена на рис. П18.

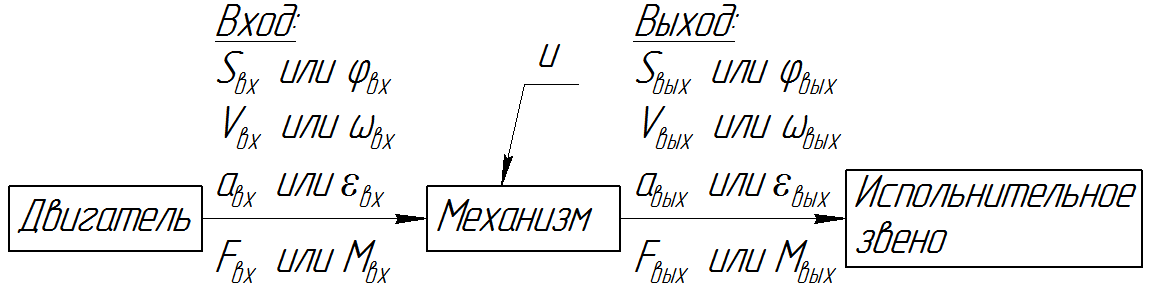
Рис. П18. Структура привода

В качестве входа и выхода привода могут рассматриваться перемещение S, скорость V, ускорение a, сила F для поступательного движения или соответственно угол поворота j, угловая скорость w, угловое ускорение e, момент М – для вращательного движения.

Передаточное отношение механизма от двигателя (входа) к исполнительному звену (выходу)

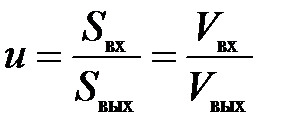. (П.60)

Отметим, что формула (П.60) соответствует «поступательному типу» входа и выхода. В случае «вращательного типа» в числителе и знаменателе должны использоваться соответствующие угловые характеристики. Например, при вращательном входе и поступательном выходе

.

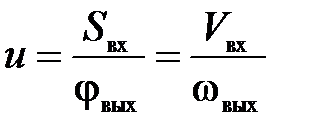Передаточное отношение механизма колеса (рис. П19)

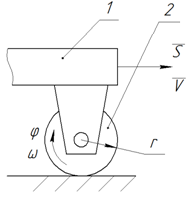
Рис. П19. Механизм колеса

1 – объект на колесах; 2 – колесо

Если колесо 2 ведущее (вход)

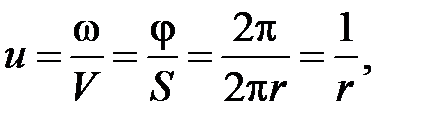
где r – радиус колеса.

Если объект 1 ведущий

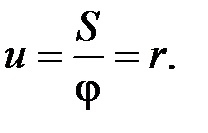
Передаточное отношение механизма с зубчатой передачей (рис. П20)

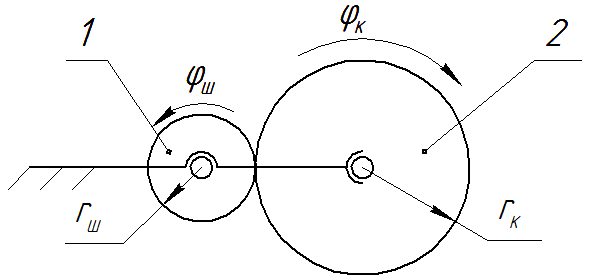
Рис. П20. Механизм с зубчатой передачей

1 – шестерня; 2 – колесо

Если шестерня ведущая

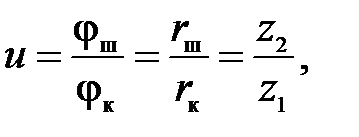
где z₁, z₂ – число зубьев на шестерне и колесе 8.

Передаточное отношение винтового механизма (рис. П21)

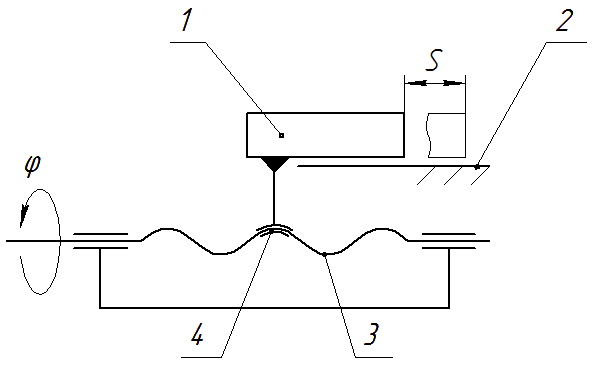
Рис. П21. Винтовой механизм

1 – ползун; 2 – направляющая; 3 – винт; 4 – гайка

Если винт ведущий

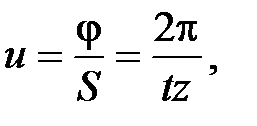
где t – шаг винта;

z – число заходов винта.

Передаточное отношение кривошипно-ползунного механизма (рис. П22)

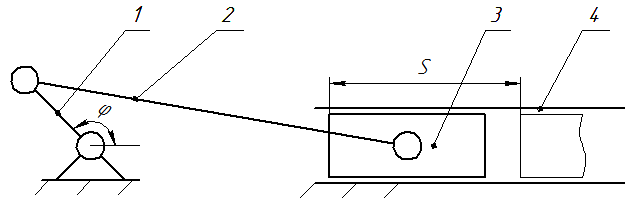
Рис. П22. Кривошипно-ползунный механизм

1 – кривошип; 2 – шатун; 3 – ползун; 4 – направляющая

Если кривошип ведущий

.

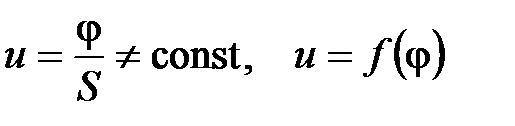Если ползун ведущий

.

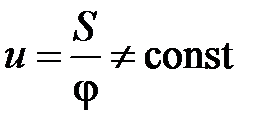Полное передаточное отношение механизма, включающего ряд последовательно соединенных механизмов с передаточными отношениями u₁, u₂,…, u_n

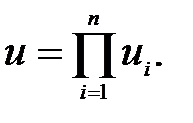. (П.61)

Пример.

Определим передаточное отношение для привода поворота платформы (рис. П23).

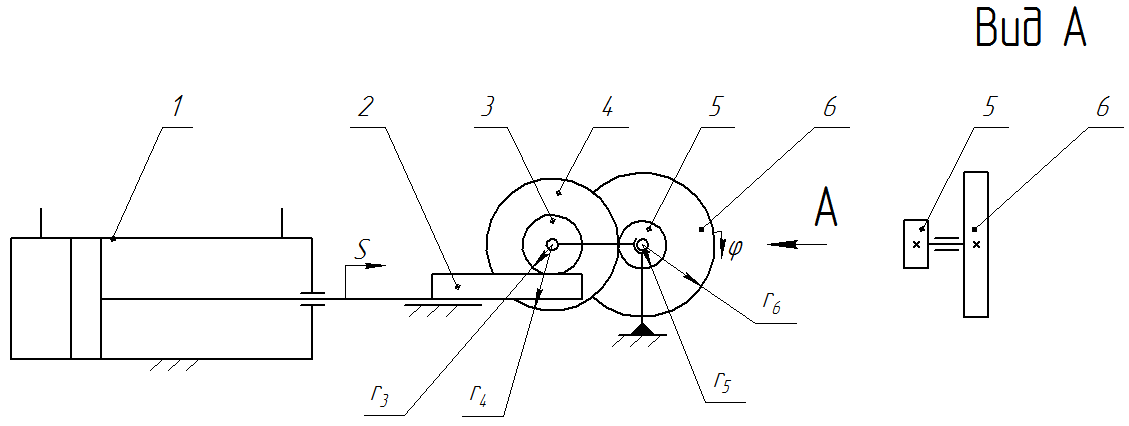
Рис. П23. Пневмопривод поворота платформы

1 – пневмоцилиндр; 2 – зубчатая рейка; 3, 4, 5 – зубчатые колеса; 6 – платформа

При перемещении штока пневмоцилиндра (двигателя) 1 на величину S платформа 6 поворачивается на угол j. Полное передаточное отношение

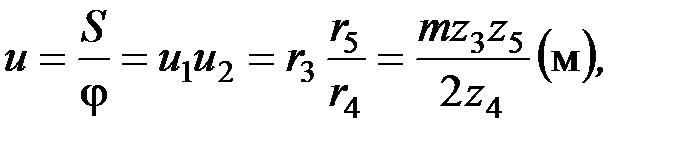
где u₁ – передаточное отношение рейка - колесо 3;

u₂ – передаточное отношение колесо 4 - колесо 5;

m – модуль в передаче рейка - колесо 3;

z₃, z₄, z₅ – числа зубьев колес 3, 4, 5.

Для схемы, представленной на рис. П18, имеем

· перемещение на двигателе

S_вх (или j_вх) = S_вых×u (или j_вых×u)

· скорость на двигателе

V_вх (или w_вх) = V_вых×u (или w_вых×u)

· ускорение на двигателе

a_вх (или e_вх) = a_вых×u (или e_вых×u)

· усилие на двигателе

F_вх (или M_вх) = F_вых/u (или M_вых/u).

Тимофеев Александр Николаевич Попов Аркадий Николаевич Полищук Михаил Нусимович