Оптимизация контура регулирования на модульный оптимум, объект которого содержит большую и малую инерционности
Дана передаточная функция объекта
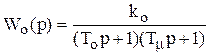 ,
,
где Т0 – большая инерционность;
Тm – малая инерционность (некомпенсированная постоянная, определяющая помехозащищенность);
k0 – коэффициент усиления объекта.
Найдем передаточную функцию регулятора 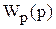 .
.
Если взять П-регулятор, то контур будет статическим, т.е. будет ошибка, стремящаяся к нулю. Для придания системе астатических свойств, а также для компенсации большой инерционности объекта подойдет ПИ-регулятор.
Передаточная функция ПИ-регулятора
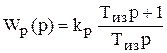 ,
,
где Тиз = Т0.
Найдем kр
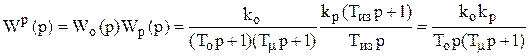 ;
;
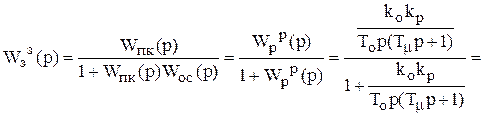
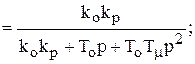
Wпк(р) = W p(p);
Woc(p) = 1;
k0kp = b0 = a0; T0 = a1; T0Tm = a2.
Из условия оптимизации на модульный оптимум 2a0a2 = a12, находим
2kpk0T0Tm = T02;
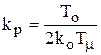 .
.
Тогда 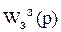 перепишется
перепишется
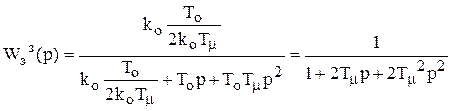 .
.
Из полученного выражения видно, что характер переходных процессов в оптимизированной замкнутой системе будет определяться малой постоянной времени Тm.
В соответствии с рисунком 5.2, на котором представлен переходный процесс в оптимизированной замкнутой системе, можно привести следующие цифры
s = 4,3% – перерегулирование;
t1 = 4,7×Tm;
t2 = 6,3×Tm;
t3 = 8,4×Tm.
Этот переходный процесс не является предельным ни по быстродействию, ни по перерегулированию.
Оптимизация по этой процедуре носит название настройки на модульный оптимум (МО).
В общем виде передаточную функцию можно представить
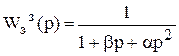 ;
;
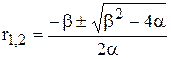 ;
;
b2 – 4a ³ 0 – переходный процесс апериодический;
b2 – 4a < 0 – переходный процесс колебательный.
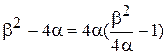 ;
;
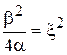 ,
,
где x – коэффициент демпфирования.
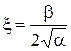 ;
;
x ³ 1 – переходный процесс апериодический;
x < 1 – переходный процесс колебательный.
В нашем случае b = 2Тm; a = 2Тm2;
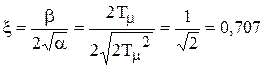 .
.
Настройка на МО является компромиссной. Быстродействие контура можно увеличить, но вместе с тем растет перерегулирование, аналогично перерегулирование можно уменьшить, но уменьшится и быстродействие (см. рисунок 5.3).
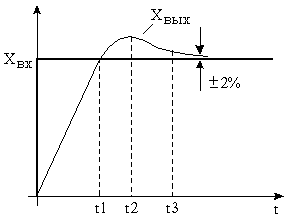 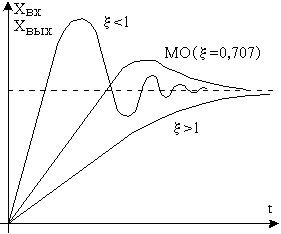 Рисунок 5.2 Рисунок 5.3 Рисунок 5.2 Рисунок 5.3 |
Настройка на модульный оптимум дает средние показатели по быстродействию и перерегулированию и легко технически реализуема.
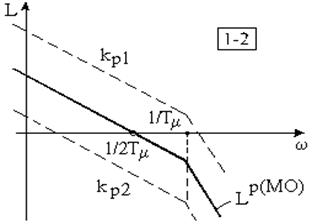 Рисунок 5.4 Рисунок 5.4 |
ЛАЧХ разомкнутого контура оптимизированного на МО представлена на рисунке 5.4.
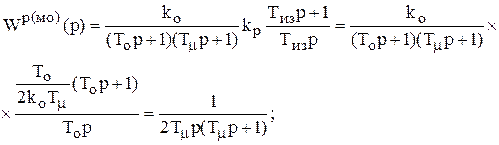
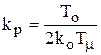 ;
;
Тиз = Т0.
Увеличение kр приведет к увеличению быстродействия, но и к повышению колебательности.
ЛАЧХ разомкнутого контура с 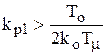 и
и 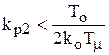 представлены на рисунке 5.4.
представлены на рисунке 5.4.
Передаточная функция замкнутого контура
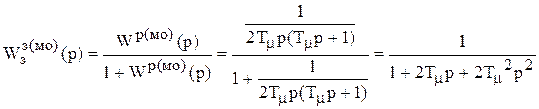 ;
;
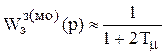 .
.
После оптимизации контура на МО контур будем представлять по упрощенному виду как апериодическое звено первого порядка (см. рисунок 5.5), а не колебательное.
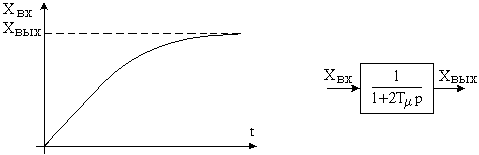 Рисунок 5.5 Рисунок 5.5 |
Порядок оптимизации на МО по ЛАЧХ (см. рисунок 5.6):
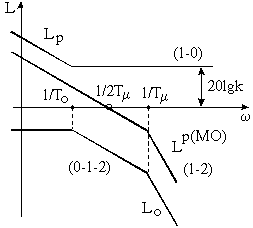 Рисунок 5.6 Рисунок 5.6 |
Дана передаточная функция разомкнутого контура
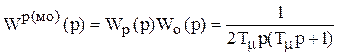 ,
,
где 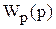 – передаточная функция регулятора;
– передаточная функция регулятора;
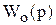 – передаточная функция объекта.
– передаточная функция объекта.
Из нее находим передаточную функцию регулятора
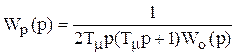 .
.
При Тиз < Т0 увеличивается площадь НЧ части характеристики, появляется участок с наклоном 40дб/дек в средней части ЛАЧХ (см. рисунок 5.7). Это приводит к увеличению быстродействия контура, но может вызвать неустойчивость в нем, если частота среза будет приходиться на участок 40дб/дек.
При Тиз > Т0 площадь НЧ части ЛАЧХ уменьшается (см. рисунок 5.8), что должно уменьшить быстродействие.
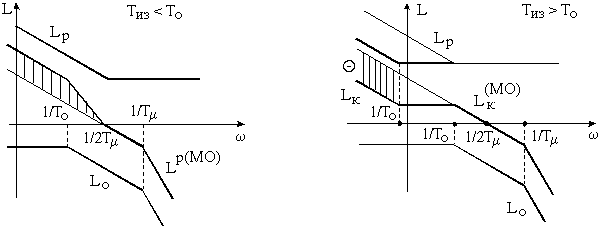 Рисунок 5.7 Рисунок 5.8 Рисунок 5.7 Рисунок 5.8 |
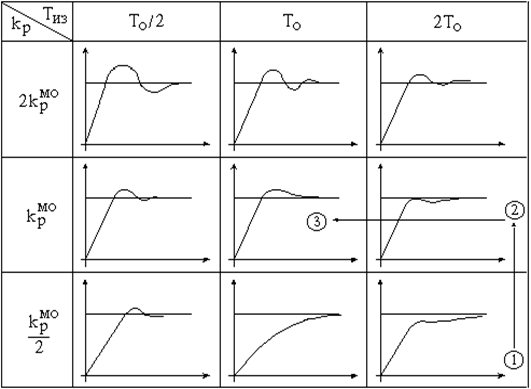 Рисунок 5.9 – Диаграммы сигналов при различных настройках контура Рисунок 5.9 – Диаграммы сигналов при различных настройках контура |
Диаграммы сигналов при различных настройках контура представлены на рисунке 5.9.
При оптимизации следующих контуров регулирования внутренний контур будет представлен апериодическим звеном.
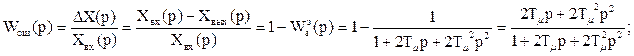
 ;
;
DХ(р) = Wош (р)×Хвх (р).
