Усталостная прочность. Виды циклов нагружения. Кривая Веллера.
К динамическим нагрузкам, несмотря на отсутствие значительных инерционных сил, можно отнести периодические многократно повторяющиеся (циклические) нагрузки, действующие на элементы конструкции.
Как показывает практика, нагрузки, циклически изменяющиеся во времени по величине или по величине и по знаку, могут привести к разрушению конструкции при напряжениях, существенно меньших, чем предел текучести (или предел прочности). Такое разрушение принято называть «усталостным». Усталостное разрушение – разрушение материала под действием повторно-переменных напряжений.
Усталость материала – постепенное накопление повреждений в материале под действием переменных напряжений, приводящих к образованию трещин в материале и разрушению.
Выносливость– способность материала сопротивляться усталостному разрушению.
Физические причины усталостного разрушения материалов достаточно сложны и еще не до конца изучены. Одной из основных причин усталостного разрушения принято считать образование и развитие трещин.
В машиностроительной практике детали машин и элементы инженерных конструкций довольно часто испытывают воздействие напряжений, переменных во времени. Рассмотрим пример. Тяжелое колесо (маховик, шкив) насажено на вал, который вращается в подшипниках с постоянной угловой скоростью 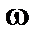 .
.
Пусть единственной нагрузкой, действующей на вал, будет вес колеса 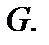 Расчетная схема вала будет представлять собой балку, нагруженную силой
Расчетная схема вала будет представлять собой балку, нагруженную силой 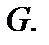 Наибольший изгибающий момент, обозначенный нами
Наибольший изгибающий момент, обозначенный нами 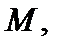 будет возникать под силой. Выясним, что будет происходить с напряжениями в некоторой точке
будет возникать под силой. Выясним, что будет происходить с напряжениями в некоторой точке  принадлежащей контуру вала. Положение этой точки будет определяться углом
принадлежащей контуру вала. Положение этой точки будет определяться углом 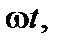 где
где  — время. Нормальные напряжения в данной точке будут равны
— время. Нормальные напряжения в данной точке будут равны
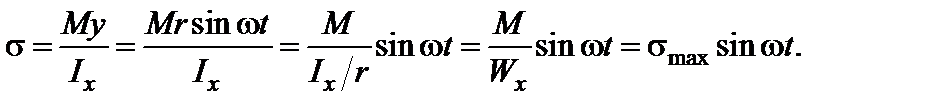
Таким образом, мы видим, что напряжения в точках контура сечения вала будут меняться по закону синуса в диапазоне
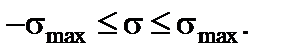
Точка, вращаясь вместе с валом, попеременно оказывается то в сжатой зоне, то в растянутой. Напряжения будут меняться циклическим образом.
Точно такая ситуация будет возникать, например, в вале редуктора, оси транспортного средства и прочих вращающихся деталях. Возникает опасность усталостного разрушения.
Виды циклов нагружения.
Усталостная прочность материалов при повторно-переменном нагружении во многом зависит от характера изменения напряжений во времени, от периодической нагрузки.
Периодическая нагрузка – переменная нагрузка с установившимся во времени характером изменения, значения которой повторяются через определенный промежуток (период) времени.
| t |
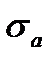 |
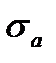 |
 |
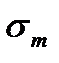 |
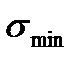 |
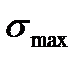 |
| Цикл напряжений. |
Обычно цикл напряжений характеризуется двумя основными параметрами цикла:
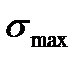 - максимальное напряжение цикла;
- максимальное напряжение цикла; 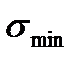 - минимальное напряжение
- минимальное напряжение
цикла;
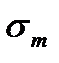 - среднее напряжение цикла:
- среднее напряжение цикла: 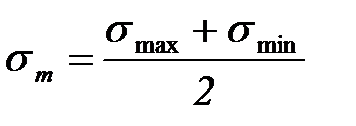 ;
;
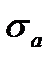 - амплитудное напряжение цикла:
- амплитудное напряжение цикла: 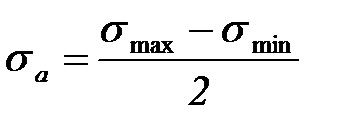 ;
;
R – коэффициент асимметрии цикла напряжении:
| t |
 |
 |
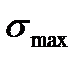 |
| Симметричный цикл. |
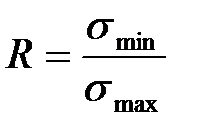 .
. В зависимости от величины перечисленных характеристик циклы напряжений могут быть подразделены на следующие основные типы:
Симметричный цикл – максимальное и минимальное напряжения равны по абсолютной величине и противоположны по знаку 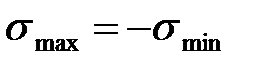 , R= –1;
, R= –1;
| t |
 |
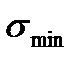 |
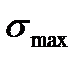 |
| Асимметричный цикл. |
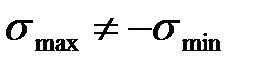 ), при этом асимметричный цикл может быть знакопеременным или знакопостоянным;
), при этом асимметричный цикл может быть знакопеременным или знакопостоянным; Знакопеременный цикл - максимальное и минимальное напряжения не равны по абсолютной величине и противоположны по знаку ( 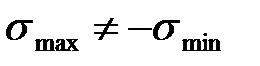 ,
, 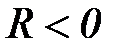 ,
, 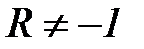 );
);
Знакопостоянный цикл - максимальное и минимальное напряжения не равны по абсолютной величине и имеют одинаковый знак ( 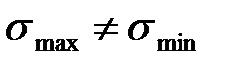 ,
, 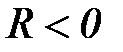 ,
, 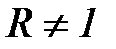 );
);
Отнулевой (пульсирующий) цикл – максимальное или минимальное напряжения равны нулю ( 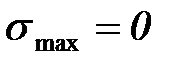 или
или 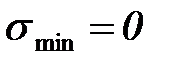 ,
, 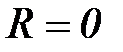 или
или 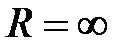 ).
).
Кривая усталости (кривая Веллера)
Кривая усталости (рис.1) строится на основании результатов усталостных испытаний при симметричном цикле.
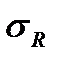 |
| N |
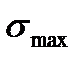 |
| Рис.1 Кривая Веллера. |
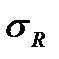 ).
). Предел выносливости (усталости) 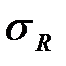 - наибольшее (предельное) напряжение цикла, при котором не происходит усталостного разрушения образца после произвольно большого числа циклов.
- наибольшее (предельное) напряжение цикла, при котором не происходит усталостного разрушения образца после произвольно большого числа циклов.
Так как испытания нельзя проводить бесконечно большое время, то число циклов ограничивают некоторым пределом, который называют базовым числом циклов. В этом случае, если образец выдерживает базовое число циклов (для черных металлов – N = 107), то считается, что напряжение в нем не выше предела выносливости.
Ударные нагрузки.
Основы расчетов на ударное нагружение. Динамический коэффициент. Случаи удара при простейших деформациях.
Явление удара получается в том случае, когда скорость рассматриваемой части конструкции или соприкасающихся с ней частей изменяется в очень короткий период времени.
Таким образом, в ударяемой части конструкции возникают такие напряжения, как будто к ней была приложена сила инерции ударяющего тела; мы можем вычислить эти напряжения, рассматривая силу инерции 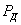 как статическую нагрузку нашей конструкции. Затруднение заключается в вычислении этой силы инерции. Продолжительности удара, т. е. величины того промежутка времени, в течении которого происходит падение скорости до нуля, мы не знаем. Поэтому остается неизвестной величина ускорения, а стало быть, и силы
как статическую нагрузку нашей конструкции. Затруднение заключается в вычислении этой силы инерции. Продолжительности удара, т. е. величины того промежутка времени, в течении которого происходит падение скорости до нуля, мы не знаем. Поэтому остается неизвестной величина ускорения, а стало быть, и силы 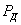 . Таким образом, хотя вычисление напряжений при ударе представляет собой частный случай задачи учета сил инерции, однако для вычисления силы
. Таким образом, хотя вычисление напряжений при ударе представляет собой частный случай задачи учета сил инерции, однако для вычисления силы 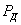 и связанных с ней напряжений и деформаций здесь приходится применять иной прием и пользоваться законом сохранения энергии.
и связанных с ней напряжений и деформаций здесь приходится применять иной прием и пользоваться законом сохранения энергии.
Применяя закон сохранения энергии, надо:
1) вычислить кинетическую энергию ударяющего тела Т;
2) вычислить потенциальную энергию 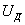 тел, воспринимающих удар, под нагрузкой их силами инерции при ударе; потенциальная энергия должна быть выражена через напряжение (
тел, воспринимающих удар, под нагрузкой их силами инерции при ударе; потенциальная энергия должна быть выражена через напряжение ( 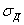 ,
, 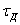 ) в каком-либо сечении, через деформацию (удлинение, прогиб) или через силу инерции
) в каком-либо сечении, через деформацию (удлинение, прогиб) или через силу инерции 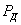 ударяющего тела;
ударяющего тела;
3) приравнять величины 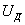 и Т и из полученного уравнения найти или непосредственно динамическое напряжение, или деформацию, а по ней, пользуясь законом Гука, напряжение или силу
и Т и из полученного уравнения найти или непосредственно динамическое напряжение, или деформацию, а по ней, пользуясь законом Гука, напряжение или силу 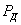 и соответствующие ей динамические напряжения и деформации.
и соответствующие ей динамические напряжения и деформации.
При ударе происходит очень быстрое превращение одного вида энергии в другой: кинетическая энергия ударяющего тела превращается в потенциальную энергию деформации. Выражая эту энергию в функции силы 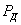 или напряжений, или деформаций получаем возможность вычислить эти величины.
или напряжений, или деформаций получаем возможность вычислить эти величины.
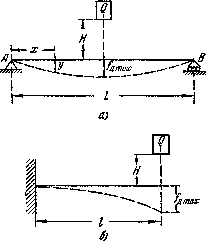
Рис.2 Модель поперечного удара.
Полагая, что кинетическая энергия Т ударяющего тела полностью переходит в потенциальную энергию 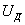 деформации упругой системы, можем написать:.
деформации упругой системы, можем написать:.
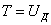 (1)
(1)
Так как к моменту окончания деформации ударяющее тело пройдет путь 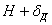 , то его запас энергии будет измеряться произведенной им работой
, то его запас энергии будет измеряться произведенной им работой 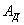 и будет равен:
и будет равен:
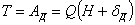
Вид формулы для 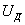 при ударе примем тот же, что и при статическом нагружении системы С силой инерции
при ударе примем тот же, что и при статическом нагружении системы С силой инерции 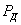 , т. е.
, т. е.
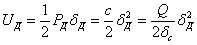
Подставляя значения Т и 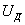 в уравнение (1), получаем:
в уравнение (1), получаем:
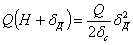 или
или
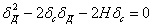
Отсюда
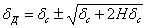 , или
, или 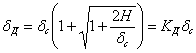
Обозначив 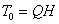 —энергия ударяющего тела к моменту начала удара, выражение для динамического коэффициента может быть представлено еще и в таком виде:
—энергия ударяющего тела к моменту начала удара, выражение для динамического коэффициента может быть представлено еще и в таком виде:
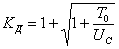
Формулы 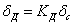 и
и 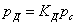 , в которых
, в которых 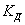 выражается через
выражается через 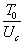 , могут быть использованы также для решения задачи о встречном ударе тел, двигающихся с некоторой скоростью.
, могут быть использованы также для решения задачи о встречном ударе тел, двигающихся с некоторой скоростью.
Описанный общий прием расчета на удар предполагает, что вся кинетическая энергия ударяющего тела целиком переходит в потенциальную энергию деформации упругой системы. Это предположение не точно. Кинетическая энергия падающего груза частично превращается в тепловую энергию и энергию неупругой деформации основания, на которое опирается система.
Вместе с тем при высоких скоростях удара деформация за время удара не успевает распространиться на весь объем ударяемого тела и в месте удара возникают значительные местные напряжения, иногда превосходящие предел текучести материала.
Рассмотрим некоторые случаи удара при простейших деформациях. При этом для нахождения коэффициента динамичности применим основные полученные формулы для динамического коэффициента.
Для определения 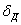 ,
, 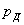 и
и 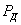 используем зависимости:
используем зависимости:
 и
и 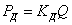
При изгибе величина статической деформации 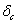 , представляющей собой статический прогиб балки
, представляющей собой статический прогиб балки 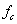 с в месте удара, зависит от схемы нагружения и условий опирания балки.
с в месте удара, зависит от схемы нагружения и условий опирания балки.
Так например, для для консоли, испытывающей удар от груза Q, падающего на свободный конец консоли с высоты Н (Рис 1):
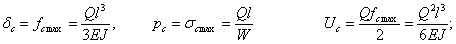
Подставляя в формулу для коэффициента динамичности 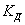 значения
значения 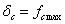 или
или 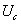 , находим
, находим 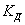 , а затем и величину динамических напряжений и деформаций.
, а затем и величину динамических напряжений и деформаций.
Имея в виду, что
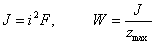 и
и 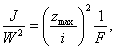
можем представить выражение для 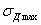 еще и в таком виде:
еще и в таком виде:
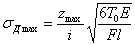
Из последней приближенной формулы видно, что динамические напряжения при изгибе балки зависят от модуля упругости материала, объема балки, формы ее поперечного сечения (отношение 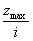 ), а также от схемы нагружения и условий опирания балки (в данном случае в подкоренном выражении стоит
), а также от схемы нагружения и условий опирания балки (в данном случае в подкоренном выражении стоит 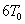 ; для балок, иначе загруженных и закрепленных, числовой коэффициент у
; для балок, иначе загруженных и закрепленных, числовой коэффициент у 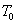 будет другим)
будет другим)
