Коэффициенты гармонической линеаризации типовых нелинейностей

Статическая характеристика нелинейного элемента
Линейная характеристика с зоной нечувствительности
Линейная характеристика с ограничением
Линейная характеристика с зоной нечувствительности и ограничением
Характеристика «люфт»
Идеальная релейная характеристика
Однозначная релейная характеристика с зоной нечувствительности
Неоднозначная релейная характеристика с зоной нечувствительности
Кубическая парабола:
Характеристика «петля гистерезиса»

Передаточная функция нелинейного эле­мента имеет существенное отличие от передаточной функ­ции линейной системы , заключающееся в том, что зависит от амплитуды и частоты входного сигнала.

Выражение (8.22) запишем в виде:

q(A) + q₁(A), (8.23)

где q(A), q₁(A) – коэффициенты гармонической линеаризации, определяемые как отношения коэффициентов ряда Фурье для пер­вой гармоники выходных колебаний к амплитуде вход­ных колебаний:

q(A) = q₁(A) = . (8.24)

Заменяя в выражении (8.23) р на , получим выражение для комплексного коэффициента передачи нелинейного элемента:

q(A) +j q₁(A), (8.25)

являющегося аналогом АФХ для линейного звена.

В качестве примера определим выражение для комплексного коэффициента передачи нелинейного элемента с релейной статической характеристикой (8.14). Коэффициенты ряда Фурье A₁ и B₁ для указанной нелинейности равны:

;

B₁ .

Очевидно, что коэффициент B₁ будет равен нулю для любого нелинейного элемента с нечетно-симметричной статической нелинейностью.

Тогда, согласно выражениям (8.24) и (8.25) получим:

q(A) = ; q₁(A) = 0 и W(A) = .

Значения коэффициентов гармонической линеаризации для нескольких типовых нелинейностей приведены в таблице 8.1.

8.5. Методы определения параметров автоколебаний

Если в замкнутой нелинейной системе САУ возникают автоколебания с постоянной амплитудой и частотой, то коэффициенты гармонической линеаризации оказывают­ся постоянными, а вся система стационарной. Незатуха­ющие колебания в замкнутых системах возникают в том случае, когда характеристиче­ское уравнение системы содержит пару мнимых сопря­женных корней.

Характеристический полином замкнутой системы (рис.8.1) при осуществлении гармонической линеаризации входящего в нее нелинейного звена запишем в виде:

, (8.26)

где —передаточная функция линейной части си­стемы; —передаточная функция нелинейного элемента после его линеаризации.

Если , то выражение (8.26) можно записать в виде:

. (8.27)

Заменяя в выражении (8.27) р на , по­лучим комплексное выражение, в котором необходимо выделить вещественную и мнимую части:

[ q(A) +j q₁(A)] . (8.28)

При этом условие возникновения периодических колебаний в системе с частотой и амплитудой запишем:

(8.29)

Если решения системы (8.29) комплексные или отрицательные, режим автоколебаний в системе невозможен. Наличие положительных вещественных решений для и свидетельствует о наличии в системе автоколебаний, которые необходимо проверить на устойчивость.

В качестве примера найдем условия возникновения автоколеба­ний в САУ, если передаточная функция ее линейной части равна:

(8.30)

и нелинейным элементом типа «петля гистерезиса».

Передаточная функция гармонически линеаризованного нелинейного элемента (см. табл. 8.1) имеет вид:

. (8.31)

Подставляя выражения (8.30) и (8.31) в выражение (8.26) и заменяя р на , найдем выражение для :

.

Отсюда в соответствии с выражением (8.29) получаем следующие условия возникновения автоколебаний в системе:

Решение системы уравнений (8.29) обычно затруднительно, так как ко­эффициенты гармонической линеаризации имеют слож­ную зависимость от амплитуды входного сигнала. Кроме того, помимо определения амплитуды и частоты , необходимо оценить устойчивость автоколебаний в системе.

Условия возникновения автоколебаний в нелинейной системе и параметры предельных циклов можно исследо­вать, используя частотные критерии устойчивости, например, критерий устойчи­вости Найквиста. Согласно этому критерию при наличии автоколебаний амплитудно-фазовая характеристика разомкнутой гармонически линеаризованной системы, равная

= ,

проходит через точку (-1, j0). Следовательно, для и справедливо равенство:

или

. (8.32)

Решение уравнения (8.32) относительно частоты и амплитуды автоколебаний можно получить графически. Для этого на комплексной плоскости необходимо, изменяя частоту от 0 до , построить годограф АФХ линейной части системы и, изменяя амплитуду А от 0 до , построить годограф обратной ха­рактеристики нелинейной части , взятый с знаком «минус». Если эти годографы не пересекаются, то режим автоколебаний в исследуемой системе не существует (рис. 8.18, б).

Рис. 8.18. К определению наличия и устойчивости автоколебаний в нелинейной системе

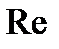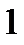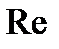а)

б)

При пересечении годографов (рис. 8.18, а) в системе возникают автоколебания, частота и амплитуда которых опреде­ляются значениями и в точке пересечения.

Если и - пересекаются в нескольких точках (рис. 8.18, а), то это свидетельствует о наличии в системе нескольких предельных циклов. При этом колебания в системе могут быть устойчивы­ми и неустойчивыми.

Устойчивость автоколебательного режима оценивается следующим образом. Режим автоколебаний устойчив, если точка на годографе нелинейной части , соответствующая амплитуде большей по сравнению со значением в точке пересечения годографов, не охватывается годографом частотной характеристики линейной части системы. В противном случае автоколебательный режим неустойчив.

На рис. 8.18, а годографы пересекаются в точках 1 и 2. Точка 1определяет неустойчивый режим автоколебаний, так как точка годографа , соответствующая увеличенной амплитуде, охватывается годографом частотной характеристики линейной части системы. Точке 2 соответствует устойчивый режим автоколебаний, амплитуда которых определяется по годографу а частота – по годографу .

В качестве примера оценим устойчивость автоколебаний в двух нелинейных системах. Будем полагать, что передаточные функции линейных частей этих систем совпадают и равны:

,

но входящие в них их нелинейные элементы различны. Пусть в первую систему включен нелинейный элемент «идеальное реле», описываемый системой (8.14), а во вторую – нелинейный элемент со статической характеристикой «кубическая парабола». Воспользовавшись данными таблицы 8.1, получим:

и – .

Рис. 8.19. К оценке устойчивости автоколебаний

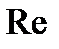а)

б)

На рис. 8.19 изображены годографы этих систем совместно с годографом АФХ линейной части системы . На основании изложенного можно утверждать, что в первой системе возникают устойчивые автоколебания с частотой и амплитудой , а во второй системе автоколебания неустойчивые.

Вопросы для самопроверки

1. Сформулируйте принцип суперпозиции.

2. Назовите несколько причин, обуславливающих нелинейность САУ.

3. Перечислите методы, позволяющие решать задачи анализа и синтеза нелинейных систем.

4. С чем связано ограничение на использование фазовой плоскости для описания динамики нелинейных систем?

5. Что называется фазовой траекторией?

6. Назовите общие закономерности, которым удовлетворяют фазовые траектории нелинейных систем.

7. Перечислите типы особых точек на фазовой траектории.

8. Что называется предельным циклом на фазовой траектории?

9. С чем связано ограничение метода гармонической линеаризации?

10. Как могут быть определены параметры автоколебаний и их устойчивость?

Курсовая работа

Цель курсовой работы – закрепить теоретический материал и освоить методику анализа САУ.

В рамках курсовой работы не ставится задача проек­тирования CAУ для конкретного технологического процесса, так как подобные задачи решаются в последующих кур­сах специальности. В выполняемой курсовой работе математическое описание и структура системы заданы. Требуется, используя методы теории уп­равления, обеспечить необходимые статические и динамические показатели качества регулирования системы путем введения в нее корректирующих звеньев.

Приведенные методические рекомендации по решению основных задач, решаемых в рамках курсовой работы, но они не являются обязательными. Можно выбрать другие обоснованные методы их решения. Курсовая работа включает в себя два раздела: расчет линейной и нелинейной систем автоматичес­кого регулирования.

Курсовая работа представляется к проверке в виде расчетно-пояснительной записки, содержащей вариант задания, расчетные формулы и соотношения, список использован­ной литературы, на которую должны быть сделаны ссылки в тексте, расчеты и необходимые пояснения к ним, выводы на основа­нии полученных результатов.

После проверки курсовой работы преподавателем, необходимо устранить замечания (если это требуется) и защитить её. Во время защиты следует обосновать принятые решения и полученные результаты, объяснить формулы, характеристики и графики, знать теоретические разделы курса, использованные в работе.

Номер варианта задания равен сумме трех последних цифр учебного шифра студенческого билета.

Задание для расчета линейной CAУ

Дана структурная схема линейной САУ

1. Проанализировать устойчивость замкнутой сис­темы, используя прямой метод оценки устойчивости и произвольно выбранный критерий устойчивости.

2. Провести синтез последовательного и параллельного корректирующих звеньев, обеспечивающих следующие показа­тели качества процесса регулирования в скорректированной системе:

a) перерегулирование σ ≤ 25 %;

б) длительность переходного процесса, не превышающую значения t_рег, в соответствие с вариантом задания;

в) точность скорректированной системы должна быть не ниже точности нескорректированной САУ.

3.

_

Рассчитать точность скорректированной системы по управляющему и возмущающему воздействиям в установившемся режиме.

4. Определить критическое время запаздывания, при котором скорректированная система будет находиться на границе устойчивости.

Варианты задания для расчета линейной САУ

Вариант задания	Варианты W(p									ξ	tр
						0,1	0,025	0,002	0,001	-	0,15
					4,5	0,225	0,002	-	0,001	0,8	0,1
						-	0,0001	0,5	0,0001	-	0,5
						-	0,175	0,001	0,002	0,8	0,1
						0,001	0,07	0,001	-	-	0,4
						0,007	0,125	-	0,0015	0,8	0,3
						-	0,0025	0,05	1,2	0,8	0,3
						0,5	0,07	0,003	0,001	-	0,2
						1,2	0,0025	-	0,05	0,8	0,3
			2,5			-	0,002	0,2	0,002	-	0,3
						-	0,125	0,001	0,002	0,8	0,1
				0,5		0,001	0,1	0,001	-	-	0,8
						0,001	0,2	-	0,0025	0,8	0,1
						-	0,0025	0,001	0,2	0,8	0,1
							0,13	0,006	0,001	-	0,3
			0,5		0,5		0,001	-	0,004	0,8	0,5
		2,5				-	0,001	0,3	0,001	-	0,3
		0,2	0,2			-	0,65	0,005	0,001	0,8	0,3
		2,5		0,4		0,001	0,9	0,001	-	-	1,5
						0,005	0,5	-	0,0025	0,8	0,5
						-	0,002	0,001	0,15	0,8	0,1
						0,38	0,135	0,005	0,001	-	0,3
						0,25	0,001	-	0,004	0,8	0,3
				2,5		-	0,001	0,1	0,001	-	0,6
						-	0,005	12,5	0,001	0,8	0,3
				3,5		0,001		0,001	-	-	1,5
						0,12	0,008	-	0,0015	0,8	0,3
						-	0,002	0,001	0,2	0,8	0,1

Варианты передаточных функций линейной САУ

Варианты W(p)

Задание для расчета нелинейной САУ

1. Исследовать динамические режимы системы методом фазовой плоскости для заданной статической характеристики нелинейного элемента (НЭ).

2. Построить переходный процесс по полученной фазовой траектории.

3. Определить наличие автоколебаний в системе, оценить их устойчивость и рассчитать параметры.

Варианты задания для расчета нелинейной САУ

Вариант задания	Варианты структуры и нелинейного элемента						h	a	b
			-	-	0,8	0,4			-
					-	-			-
						-
			-	-	0,7	0,8			-
					-	-			-
						-
			-	-		0,8			-
				2,5	-	-			-
						-
			-	-		0,8			-
					-	-			-
						-
			-	-		0,6			-
					-	-			-
						-
		0,5	-	-	0,8	0,6			-
				2,5	-	-			-
						-
			-	-	0,5	0,8			-
					-	-			-
						-
			-	-		0,15			-
					-	-			-
						-
			-	-		0,2			-
					-	-			-
						-
			-	-	1,5	0,3			-

Варианты структурных схем нелинейных систем

2)

1)

3)

Варианты статических характеристик нелинейного элемента

1)

3)

2)

Экзаменационные вопросы

1. Классификация систем автоматического управления.

2. Принципы линеаризации систем автоматического управления.

3. Использование дифференциальных и операторных уравнений при описании систем автоматического управления. Основные свойства преобразования Лапласа.

4. Передаточные функции систем автоматического управления.

5. Временные характеристики систем автоматического управления.

6. Частотные характеристики систем автоматического управления.

7. Характеристики пропорционального звена

8. Характеристики идеального дифференцирующего звена.

9. Характеристики апериодического звена первого порядка.

10. Характеристики реального дифференцирующего звена.

11. Характеристики инерционного звена второго порядка.

12. Характеристики звена чистого запаздывания.

13. Характеристики интегро-дифференцирующего звена.

14. Характеристики пропорционально-интегрирующего звена.

15. Эквивалентные преобразования структурных схем линейных систем автоматического управления.

16. Понятие устойчивости линейных систем автоматического управления. Необходимое и достаточное условия устойчивости. Прямой метод оценки устойчивости.

17. Алгебраический критерий устойчивости Гурвица.

18. Частотный критерий устойчивости Михайлова. Принцип аргумента.

19. Частотный критерий устойчивости Найквиста.

20. Устойчивость систем с запаздыванием.

21. Оценка качества процесса регулирования по переходной характеристике системы.

22. Частотные критерии качества.

23. Корневые критерии качества.

24. Интегральные критерии качества.

25. Оценка точности систем автоматического управления. Статические и астатические системы.

26. Коэффициенты ошибки системы.

27. Системы комбинированного управления.

28. Типы корректирующих звеньев в системах автоматического управления.

29. Частотный метод синтеза корректирующих устройств.

30. Последовательные корректирующие устройства..

31. Параллельные корректирующие устройства.

32. Техническая реализация корректирующих устройств.

33. Особенности нелинейных систем и методы их анализа.

34. Исследование нелинейных систем на фазовой плоскости.

35. Метод гармонической линеаризации нелинейных звеньев.

36. Методы определения параметров автоколебаний.

Литература

1. Теория автоматического регулирования: Учеб. пособие/ А.С.Востриков, Г.А.Французова - М.: Высшая школа, 2004.- 365 с.

2. Пупков К.А., Егупов Н.Д., Баркин А.И. и др. Методы классической и современной теории автоматического управления. В 5 томах. Том 1. Математические модели, динамические характеристики и анализ систем автоматического управления. – М.: Издательство МГТУ им. Н. Э. Баумана, 2004 – 656 с.

3. Теория автоматического управления: Учебник для вузов/ С.Е. Душин,

Н.С. Зотов, Д.Х. Имаев и др.; Под ред. В.Б.Яковлева.– М.: Высшая школа, 2003.– 567 с.

4. Мирошник И.В. Теория автоматического управления. Линейные системы. – СПб.: Питер, 2005. – 336 с.: ил.

5. Пупков К.А., Егупов Н.Д., Баркин А.И. и др. Методы классической и современной теории автоматического управления. В 5 томах. Том 2. Статистическая динамика и идентификация систем автоматического управления . – М.: Издательство МГТУ им. Н. Э. Баумана, 2004 – 656 с.

6. Мирошник И. В. Теория автоматического управления. Часть 2. Нелинейные и оптимальные системы. – СПб.: Питер, 2005. – 336 с.: ил.

7. Никулин Е. А. Основы теории автоматического управления. Частотные методы анализа и синтеза систем. – СПб.: БХВ-Петербург, 2004. – 640 с.

8. Теория автоматического управления: Учебное пособие для ВУЗов/ Анхимюк В. Л., Опейко О. Ф., Михеев Н. Н. – М.: Дизайн ПРО, 2002. – 352 с.

9. Ерофеев А.А. Т