Сочетания без повторений и с повторениями
Цель: Изучить на практике методику расчета числа сочетаний без повторений и с повторениями
.Содержание:
Задание 11(на число сочетаний без повторений).
Задание 12(начисло сочетаний с возможными повторениями).
Задание 13 (начисло сочетаний с обязательными повторениями).
Задание 11(начисло сочетаний без повторений).
Сколько различных подарков по m различных предметов в каждом можно составить, выбирая предметы без повторения из следующего набора n=5 штук разных предметов: 1-яблоко,3 - слива, 5 - груша, 7 - апельсин, 9 - банан? Решить задание для m=3
ЧИСЛО СОЧЕТАНИЙ БЕЗ ПОВТОРЕНИЙ.КРАТКАЯ ТЕОРИЯ
Сочетаниями без повторений или просто сочетаниями элементов n различных типов по т называются их неупорядоченные наборы из m различных элементов, отличающиеся друг от друга только самими элементами.
При этом т < n, поскольку не допускается повторение элементов в их неупорядоченном наборе из т элементов. (Здесь и далее под неупорядоченным набором из т элементов понимается их линейно неупорядоченное множество, аналогичное множеству разноцветных шаров, помещенных в урну, причем нет никакого порядка в их взаимном расположении.)
Число всех сочетаний элементов п различных типов по неупорядоченным наборам из т различных элементов (обозначается 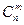 ) есть
) есть 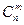 =
= 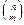 =n!/(m!(n-m)!) (числа
=n!/(m!(n-m)!) (числа 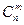 часто называют биномиальными коэффициентами).
часто называют биномиальными коэффициентами).
КОНЕЦ ТЕОРИИ.
Решение.
В задании 11m=3, n=5. Тогда по формуле имеем 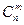 = n!/(m!(n-m)!). Подставляя в формулу m=3 и n=5, имеем
= n!/(m!(n-m)!). Подставляя в формулу m=3 и n=5, имеем 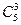 = 5!/(3)!(5-3)!)= 5!/((3)!2!)=120/(6×2)=10.
= 5!/(3)!(5-3)!)= 5!/((3)!2!)=120/(6×2)=10.
Ответ: 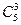 =10, т. е 10 различных подарков по m=3 различных предметов в каждом можно составить, выбирая предметы без повторения из следующего набора n=5 предметов
=10, т. е 10 различных подарков по m=3 различных предметов в каждом можно составить, выбирая предметы без повторения из следующего набора n=5 предметов
Задание 12(начисло сочетаний с возможными повторениями).
Сколько различных подарков по m предметов в каждом можно составить, выбирая предметы с возможностью повторения из следующего набора n=5 штук разных предметов: 1-яблоко,3 - слива, 5 - груша, 7 - апельсин, 9 - банан? Решить задание для m=3.
ЧИСЛО СОЧЕТАНИЙ С ВОЗМОЖНЫМИ ПОВТОРЕНИЯМИ.КРАТКАЯ ТЕОРИЯ
Сочетаниями с повторениями элементов n различных типов по т называются их неупорядоченные наборы из т элементов, отличающиеся друг от друга только самими элементами.
При этом возможно и т ≤ п, и т > п,поскольку допускается повторение элементов в их неупорядоченном наборе из т элементов.
Число всех сочетаний с повторениями элементов л различных типов по неупорядоченным наборам из т элементов (обозначается 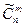 ) есть
) есть 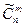 =
= 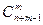 =
= 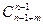 .
.
КОНЕЦ ТЕОРИИ.
Решение.
В задании 12m=3, n=5. Тогда по формуле имеем 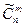 =
= 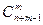 =(n+m-1)!/(m!(n-1)!). Подставляя в формулу m=3 и n=5, имеем
=(n+m-1)!/(m!(n-1)!). Подставляя в формулу m=3 и n=5, имеем 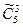 =(5+3-1)!/(3! (5-1)!)==7!/((3)!4!)=5040/(6×24)= 35.
=(5+3-1)!/(3! (5-1)!)==7!/((3)!4!)=5040/(6×24)= 35.
Ответ: 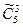 =35, т. е. 35 различных подарков по m=3 предмета в каждом можно составить, выбирая предметы с возможностью повторения из набора n=5 штук разных предметов.
=35, т. е. 35 различных подарков по m=3 предмета в каждом можно составить, выбирая предметы с возможностью повторения из набора n=5 штук разных предметов.
Задание 13(начисло сочетаний с обязательными повторениями).
Сколько различных подарков по m предметов в каждом можно составить, выбирая предметы с обязательными повторениями из следующего набора n=5 штук разных предметов: 1-яблоко,3 - слива, 5 - груша, 7 - апельсин, 9 - банан? Решить задание для m=3.
ЧИСЛО СОЧЕТАНИЙ С ОБЯЗАТЕЛЬНЫМИ ПОВТОРЕНИЯМИ.КРАТКАЯ ТЕОРИЯ
Пусть A - множество сочетаний элементов с возможными их повторениями из n по m элементов, B - множество сочетаний элементов без возможности их повторениями из n по m элементов. Очевидно, число элементов n(A) множества A равно 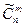 , а числоэлементов n(B) множества B равно
, а числоэлементов n(B) множества B равно 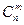 . Так как множество B есть подмножество множества A, то BÌA, поэтому число элементов их пересечения равно n(A∩B)=n(B)=
. Так как множество B есть подмножество множества A, то BÌA, поэтому число элементов их пересечения равно n(A∩B)=n(B)= 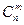 . Наконец, пусть A\B - множество сочетаний элементов с обязательными повторениями из n по m элементов. Тогда по следствию из правила суммы число элементов последнего множества A\B равно n(A\B)= =n(A)-n(A∩B)=
. Наконец, пусть A\B - множество сочетаний элементов с обязательными повторениями из n по m элементов. Тогда по следствию из правила суммы число элементов последнего множества A\B равно n(A\B)= =n(A)-n(A∩B)= 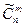 -
- 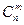 .
.
КОНЕЦ ТЕОРИИ.
РЕШЕНИЕ.
В задании 13m=3, n=5. Тогда по формуле имеем n(A\B)= 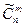 -
- 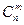 =
= 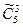 -
- 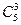 =35-10=25.
=35-10=25.
Ответ: n(A\B)= 25, т. е 25 различных подарков по m=3 предметов в каждом можно составить, выбирая предметы с обязательным повторением из набора n=5 штук разных предметов.
ЗАНЯТИЕ 6.
РАЗМЕЩЕНИЯ И СОЧЕТАНИЯ БЕЗ ПОВТОРЕНИЙ И С ПОВТОРЕНИЯМИ НА ПРИМЕРЕ БРОСАНИЯ ИГРАЛЬНЫХ КОСТЕЙ.
Цель: Изучить на практике методику вычисления количества размещений и сочетаний без повторений и с повторениями на примере бросания игральных костей
.Содержание:
Задание 14 (на число размещений и сочетаний на примере бросания игральных костей).
Задание 14 (на число размещений и сочетаний на примере бросания игральных костей).
Брошены наудачу m штук правильных n-гранников, на каждой грани которых нанесены точками последовательные натуральные числа от 1 до n (игральные “кубики”) (см. параграф ”Тела Платона”). Сколько при этом возможно результатов бросания в следующих случаях:
1) все m штук правильных n-гранников разные (например разного цвета), а учитываются только разные (неодинаковые, неповторяющиеся) числа, выпавшие на них,
2) все m штук правильных n-гранников разные (например разного цвета), а учитываются только в том числе и одинаковые (повторяющиеся) числа, выпавшие на них,
3) все m штук правильных n-гранников разные (например разного цвета), а учитываются обязательно одинаковые (повторяющиеся) числа, выпавшие на них,
4) все m штук правильных n-гранников одинаковые, а учитываются только разные (неодинаковые, неповторяющиеся) числа, выпавшие на них,
5) все m штук правильных n-гранников одинаковые, а учитываются только в том числе и одинаковые (повторяющиеся) числа, выпавшие на них,
6) все m штук правильных n-гранников одинаковые, а учитываются обязательно одинаковые (повторяющиеся) числа, выпавшие на них?
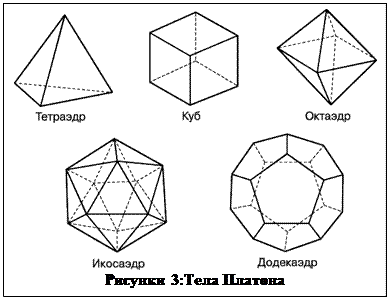
Замечание.В качестве правильных n-гранников в этом задании могут быть выбраны любые из 5 тел Платона, показанные на рис. 3 (n=4 - тетраэдр, n=6 – гексаэдр или куб, n=8 - октаэдр, n=12 - додекаэдр, n=20 - икосаэдр). Решить задание например для n=6 и m=2.
Решение
Данное задание - на число размещений и сочетаний на примере бросания игральных костей.Ее решение дано в виде таблицы ниже:
| Тип учитываемых чисел¯ | Тип используемых n-гранников ¯ | |
| Все разные | Все одинаковы | |
| Все разные=запрещеныодинаковые | 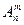 решает п. 1 задания 14 решает п. 1 задания 14 | 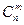 решает п. 4 задания 14 решает п. 4 задания 14 |
| Возможны одинаковые | 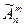 решает п. 2 задания 14 решает п. 2 задания 14 | 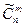 решает п. 5 задания 14 решает п. 5 задания 14 |
| Обязательно есть одинаковые | 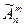 - - 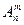 решает п. 3 задания 14 решает п. 3 задания 14 | 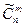 - - 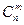 решает п. 6 задания 14 решает п. 6 задания 14 |
Решим задание например для n=6 и m=2. Имеем ответы:
Ответ на п. 1 задания 14: 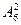 =30
=30
Ответ на п. 2 задания 14: 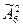 =36
=36
Ответ на п. 3 задания 14: 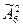 -
- 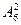 =36-30=6
=36-30=6
Ответ на п. 4 задания 14: 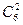 =15
=15
Ответ на п. 5 задания 14: 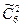 =21
=21
Ответ на п. 6 задания 14: 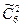 -
- 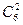 =21-15=6.
=21-15=6.
ТЕЛА ПЛАТОНА ИЛИ ПРАВИЛЬНЫЕ МНОГОГРАННИКИ. КРАТКАЯ ТЕОРИЯ
Тела Платона-это выпуклые многогранники, все грани которых правильные многоугольники. Все многогранные углы правильного многогранника конгруэнтны. Как это следует уже из подсчета суммы плоских углов при вершине, выпуклых правильных многогранников не больше пяти. Указанным ниже путем можно доказать, что существует именно пять правильных многогранников (это доказал Евклид). Они - правильный тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.
Таблица. Тела Платона
| Название: | Число ребер при вершине | Число сторон грани | Число граней | Число ребер | Число вершин |
| Тетраэдр | |||||
| Куб | |||||
| Октаэдр | |||||
| Додекаэдр | |||||
| Икосаэдр |
Тетраэдр-четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками; один из пяти правильных многоугольников.(рис. 3.1).
Куб или правильный гексаэдр - правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами.(рис.3.2).
Октаэдр-восьмигранник; тело, ограниченное восемью треугольниками; правильный октаэдр ограничен восемью равносторонними треугольниками; один из пяти правильных многогранников.(рис.3.3).
Додекаэдр-двенадцатигранник, тело, ограниченное двенадцатью многоугольниками; правильный пятиугольник; один из пяти правильных многогранников. (рис.3.4).
Икосаэдр-двадцатигранник, тело, ограниченное двадцатью многоугольниками; правильный икосаэдр ограничен двадцатью равносторонними треугольниками; один из пяти правильных многогранников(рис.3.5).
КОНЕЦ ТЕОРИИ.
ЗАНЯТИЕ 7
