Перестановки без повторений и с повторениями.

НЕУПОРЯДОЧЕННЫЕ УПОРЯДОЧЕННЫЕ РАЗБИЕНИЯС ФИКСИРОВАННЫМИ РАЗМЕРАМИ ЧАСТЕЙ

Цель: Изучить на практике методику расчета числа перестановок без повторений и с повторениями

Содержание:

Задание 4 (начисло перестановок без повторений).

Задание 5 (начисло перестановок с повторениями).

Задание 6 (начисло неупорядоченных разбиений с фиксированными размерами частей).

Задание 7 (начисло упорядоченных разбиений с фиксированными размерами частей).

Задание 4 (начисло перестановок без повторений).

Сколько различных n– значных телефонных номеров (натуральных чисел) можно написать, переставляя следующий набор n штук цифр: 1,3,5,7,9?

ЧИСЛО ПЕРЕСТАНОВОК БЕЗ ПОВТОРЕНИЙ.КРАТКАЯ ТЕОРИЯ

Перестановками без повторений или просто перестановками из элементов п различных типов называются их последовательности, отличающиеся друг от друга только порядком входящих в них элементов. (Здесь и дальше под последовательностью из п элементов понимается их линейно упорядоченное множество, аналогичное п книгам, стоящим в ряд на полке.)

Пример. Перестановки из 3 различных элементов а, b и с: аbс, bса, саb, сbа, bас, асb.

Число всех перестановок из п различных элементов (обозначается Р_п) есть Р_п= 1 • 2 • 3 •... • n = п! (п! читается "эн-факториал").

В таблице ниже приведены числовые значения факториалов первых натуральных чисел и нуля.

Таблица. Значения факториалов первых натуральных чисел и нуля.

n=
n!=

КОНЕЦ ТЕОРИИ.

Решение.

В задании 4n=5, ибо переставляются местами всевозможными способами n=5 штук различных цифр: 1,3,5,7,9. При этом каждой новой перестановке цифр соответствует новый телефонный номер (натуральное число). Поэтому искомое число различных телефонных номеров равно числу различных перестановок без повторений из n=5 штук различных элементов.

Согласно теории, искомое число равно Р₅ = 5!= 120 различных 5– значных телефонных номеров.

Ответ: 120 различных 5– значных телефонных номеров.

Задание 5 (начисло перестановок с повторениями.)

Сколько различных n– значных телефонных номеров (натуральных чисел) можно написать, переставляя следующий набор n штук цифр: 1,1,1,3,3,5?

ЧИСЛО ПЕРЕСТАНОВОК С ПОВТОРЕНИЯМИ.КРАТКАЯ ТЕОРИЯ

Перестановки с повторениями

Перестановками с повторениями из т элементов n различных типов, среди которых k₁одинаковых элементов 1-го типа, k₂одинаковых элементов 2-го типа, ... , k_nодинаковых элементов п-го типа (k₁ + k₂ + ... + k_п = m) , называются их последовательности, отличающиеся только порядком входящих в них элементов.

Пример. Перестановки из 3 элементов, среди которых 2 одинаковых элемента типа а и 1 элемент типа b: ааb, аbа, bаа.

Число перестановок из т элементов, среди которых k₁- одинаковых элементов 1-го типа, k₂ одинаковых элементов2-го типа,..., k_п- одинаковых элементов n-го типа [обозначается Р (m; k₁,k₂ ,..., k_п) ] равно:

Р (m; k₁,k₂ ,..., k_п)= т!/ (k₁!k₂ !... k_п!).

Для примера перестановок с повторениями из 3 элементов, среди которых 2 одинаковых типа а и 1 элемент типа b, имеем Р (m=3; k₁=2,k₂=1)= 3!/ (2!1!).

КОНЕЦ ТЕОРИИ.

Решение.

В задание 5m=6, ибо переставляются местами всевозможными способами m =6 штук различных цифр: 1,1,1,3,3,5, среди которых есть повторяющиеся (одинаковые). При этом каждой новой перестановке цифр соответствует новый телефонный номер (натуральное число). Поэтому искомое число различных телефонных номеров равно числу различных перестановок с повторениями из m =6 штук элементов, среди которых k₁=3 одинаковых элементов 1-го типа (цифра 1), k₂=2 одинаковых элементов2-го типа (цифра 3), k₃=1одинаковых элементов 3-го типа (цифра 5), равно Р (m; k₁,k₂ ,..., k_п)= т!/ (k₁!k₂ !... k_п!), Р(6; 3, 2, 1) = 6!/(3! 2! 1!)= =60.

Ответ: Р(6; 3, 2, 1) = 60, т. е 60 различных вариантов 6– значных телефонных номеров (6-значных чисел), содержащих цифру 1 трижды, 3 —дважды и 5 — один раз.

Задание 6 (на число неупорядоченных разбиений с фиксированными размерами частей).

Сколько всего вариантов можно получить, разбивая группу из пяти человек (из пяти солдат) на три подгруппы — две подгруппы по два человека (по два автоматчики) и одна подгруппа из одного человека (из одного пулеметчика)?

НЕУПОРЯДОЧЕННЫЕ РАЗБИЕНИЯ. КРАТКАЯ ТЕОРИЯ

Неупорядоченное разбиениеn -элементного множества X — это любое семейство {X₁, X₂,…, X_k}, где 1≤k≤п; X₁, X₂,…, X_k - непустые попарно непересекающиеся подмножества множества X , объединение которых равноX.

Называем такое разбиение неупорядоченным, таккак семейство — это неупорядоченнаясовокупность.

Пример.Для множества {а,b,с} неупорядоченное разбиение это, например, {{а},{b,с}}. Причем {{а},{b,с}}={{b,с},{а}}.

Для множества с п элементами обозначим через D(n; k₁, k₂,…, k_n) число всех таких неупорядоченных разбиений,в которых есть k₁ подмножеств с однимэлементом, k₂ подмножеств с двумяэлементами и т.д., где k₁≥0, k₂≥0,…, k_n≥0; k₁+2 k₂+…+n k_n= n.

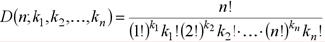Имеем

КОНЕЦ ТЕОРИИ.

Решение.

Каждый вариант— это неупорядоченное разбиение { Иванов, Петров, Сидоров, Андреев, Борисов }. Множество из 5 элементов Один из вариантов разбиения {{Иванов, Петров}, {Сидоров, Андреев}, {Борисов}}

Имеем п = 5, k₁=1, k₂=2, k₃=0, k₄=0, k₅=0 (так как по условию нет подгрупп из трех, четырех, пяти человек).

Получим

Ответ: 15 вариантов.

Задание 7 (начисло упорядоченных разбиений с фиксированными размерами частей).

Сколькими способами можно выбрать из десяти солдат трех пулеметчиков, трех гранатометчиков и четырех автоматчиков (3 пулеметчика 3 гранатометчика 4 автоматчика, всего 10 солдат)?

УПОРЯДОЧЕННЫЕ РАЗБИЕНИЯ.КРАТКАЯ ТЕОРИЯ

Упорядоченным разбиениемконечного множества X с n элементами называется любой кортеж вида <X₁, X₂,…, X_k>, где 1 ≤k ≤n; X₁, X₂,…, X_k - непустые попарно непересекающиеся, подмножества множества X, объединение которых равно X.

Называем такое разбиение упорядоченным, так как элементы кортежа упорядочены.

Пример.Для множества {а,b,с} упорядоченное разбиениеэто, например, кортеж <{{а},{b,с}}>.Причем <{{а},{b,с}}>¹<{{b,с},{а}}>.

Для множества с п элементами обозначим через E(n; m₁, m₂,…, m_k,) число всех таких упорядоченных разбиений на подмножества X₁, X₂,…, X_k, содержащие m₁, m₂,…, m_k, где m ₁≥0, m ₂≥0,…, m _k≥0; m ₁+ m ₂+…+ m _k= n.

Число всех упорядоченных разбиений<X₁, X₂,…, X_k> множества с п элементами на подмножества X₁, X₂,…, X_k, содержащие m₁, m₂,…, m_k, элементов соответственно. определяется по полиномиальной формуле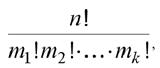

где m₁≥1, m₂≥1,…, m_n≥1; m₁+ m₂+…+m_k= n.

КОНЕЦ ТЕОРИИ.

Решение.

В задании имеем упорядоченное разбиение <X₁, X₂, X₃>множества с десятьюэлементами, где X₁ - подмножество пулеметчиков,Х₂ — подмножество гранатометчиков,Х₃ — подмножество автоматчиков;

поэтому п = 10, m₁ = 3, т₂, = 3, т₃ = 4.

Тогда всего есть

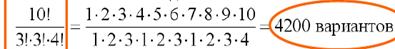
Ответ: 4200 вариантов

ЗАНЯТИЕ 4.