Правило суммы и произведения в комбинаторике
ЗАНЯТИЕ 1.
ОПЕРАЦИИ И ОТНОШЕНИЯ НАДПРОСТЫМИ И СЛОЖНЫМИ МНОЖЕСТВАМИ
Цель: Изучить на практике методику выполнения операций над простыми и сложными множествами
.Содержание:
Задание 1. Выполнить операции над простыми и сложными множествами, заданными ниже в табл. 1, и найти отношения между ними.
Табл. 1.
| Задание 1. Даны множества… | |
| …букв (простые множества): | …треугольников (сложные множества): |
| A={л,и,с,а} | A-прямоугольных |
| B={а,и,с,т} | B-равнобедренных |
| C={к,р,о,т} | C-с углом 540 |
| D={к,о,т } | D-со стороной 10 см |
| E={в,о,л,к} | E-тупоугольных |
| F={з,а,я,ц} | F-равносторонних |
| G={е,ж,и,к} | G-имеющих площадь 10 кв. см. |
| H={р,е,п,а} | H- имеющих периметр 10 см |
| K={м,ы,ш,ь} | K- вписанных в окружность радиусом 10 см |
| U- всех русских букв | U- всех возможных треугольников |
Выполнить операции над множествами:
| Вариант номер | Задание варианта |
| 1. | AÇB, A\B, B\A, AÈB, ┐A, ┐B |
| 2. | AÇC, A\C, C\A, AÈC, ┐A, ┐C |
| 3. | AÇD, A\D, D\A, AÈD, ┐A, ┐D |
| 4. | AÇE, A\E, E\A, AÈE, ┐A, ┐E |
| 5. | AÇF, A\F, F\A, AÈF, ┐A, ┐F |
| 6. | AÇG, A\G, G\A, AÈG, ┐A, ┐G |
| 7. | AÇH, A\H, H\A, AÈH, ┐A, ┐H |
| 8. | BÇC, B\C, C\B, BÈC, ┐B, ┐C |
| 9. | BÇD, B\D, D\B, BÈD, ┐B, ┐D |
| 10. | BÇE, B\E, E\B, BÈE, ┐B, ┐E |
| 11. | BÇF, B\F, F\B, BÈF, ┐B, ┐F |
| 12. | BÇG, B\G, G\B, BÈG, ┐B, ┐G |
| 13. | BÇH, B\H, H\B, BÈH, ┐B, ┐H |
| 14. | CÇD, C\D, D\C, CÈD, ┐C, ┐D |
| 15. | CÇE, C\E, E\C, CÈE, ┐C, ┐E |
| 16. | CÇF, C\F, F\C, CÈF, ┐C, ┐F |
| 17. | CÇG, C\G, G\C, CÈG, ┐C, ┐G |
| 18. | CÇH, C\H, H\C, CÈH, ┐C, ┐H |
| 19. | DÇE, D\E, E\D, DÈE, ┐D, ┐E |
| DÇF, D\F, F\D, DÈF, ┐D, ┐F | |
| DÇG, D\G, G\D, DÈG, ┐D, ┐G | |
| DÇH, D\H, H\D, DÈH, ┐D, ┐H | |
| EÇF, E\F, F\E, EÈF, ┐E, ┐F | |
| EÇG, E\G, G\E, EÈG, ┐E, ┐G | |
| EÇH, E\H, H\E, EÈH, ┐E, ┐H | |
| FÇG, F\G, G\F, FÈG, ┐F, ┐G | |
| FÇH, F\H, H\F, FÈH, ┐F, ┐H | |
| GÇH, G\H, H\G, GÈH, ┐G, ┐H | |
| AÇK, A\K, K\A, AÈK, ┐A, ┐K | |
| BÇK, B\K, K\B, BÈK, ┐B, ┐K | |
| CÇK, C\K, K\C, CÈK, ┐C, ┐K | |
| DÇK, D\K, K\D, DÈK, ┐D, ┐K |
Здесь «∩» - знак операции пересечения множеств, «\» - знак операции вычитания множеств, «È» - знак операции пересечения множеств, ┐A - знак операции дополнения множества A до универсума U. Иногда ┐A обозначают через 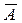 . При этом ┐A=
. При этом ┐A= 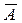 = U\A.
= U\A.
Решение.
1) Найдем пересечение X1=AÇB. Данное задание - на операции над простыми и сложными множествами
| ОПЕРАЦИЯ ПЕРЕСЕЧЕНИЯ МНОЖЕСТВ. КРАТКАЯ ТЕОРИЯ. Определение. Пересечением (или произведением) множеств А и В называется множество С, состоящее из всех тех элементов, которые принадлежат и множеству А, и множеству В. Обозначается: С = А Ç В (или С = А В). Знак Ç называется знаком пересечения. На рис. 1 пересечение множеств А и В — это область, покрытая и горизонтальной штриховкой. КОНЕЦ ТЕОРИИ. | |
| Решение для множеств букв (простые множества): | Решение для множеств треугольников(сложные множества): |
| Согласно определения С = А Ç В имеем… | |
| …Ответ на п. 1 задания 1: AÇB={и,с,а} | …Ответ на п. 1 AÇB - множество прямоугольных равнобедренных треугольников |
На рис. 1 множество X1=AÇB показано в виде «линзы» (двойного кругового сегмента) с горизонтальной штриховкой. 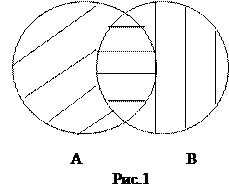 |
Решение.
2) Найдем разность X2=A\B. Данное задание - на операции над простыми и сложными множествами
ОПЕРАЦИЯ ВЫЧИТАНИЯ МНОЖЕСТВ. КРАТКАЯ ТЕОРИЯ. Результат операции вычитания множеств называют их разностью Определение. Разностью множеств А и В называется множество С, состоящее из всех тех элементов множества А, которые не являются элементами множества В. Разность множеств А и В обозначается С = А\В. При этом В может содержаться в множестве А полностью, частично или совсем не включаться. На рис. 11.5, а — в изображены эти три случая. Разность А\В каждый раз заштрихована.  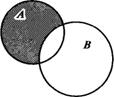 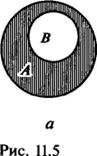
б в КОНЕЦ ТЕОРИИ. | ||||
| Согласно определения С = А\В имеем… | ||||
| Решение для множеств букв (простые множества): | Решение для множеств треугольников(сложные множества): | |||
| …Ответ на п. 2 задания 1:A\B={л} | …Ответ на п. 2 задания 1: A\B - множество прямоугольных неравнобедренных треугольников | |||
| На рис. 1 множество X2= A\B показано в виде левого полумесяца с наклонной штриховкой. | ||||
| РЕШЕНИЕ. 2) Найдем разность X2= B\A. Данное задание - на операции над простыми и сложными множествами Согласно определения C= B\A имеем… | ||||
| Решение для множеств букв (простые множества): | Решение для множеств треугольников(сложные множества): | |||
| …Ответ на п. 2 задания 1: B\A={т} | …Ответ на п. 2 задания 1: B\A - множество непрямоугольных равнобедренных треугольников. | |||
| На рис. 1 X3= B\A показано в виде правого полумесяца с вертикальной штриховкой. |
Решение.
3) Найдем разность X2= B\A. Данное задание - на операции над простыми и сложными множествами
| Согласно определения C= B\A имеем… | |
| Решение для множеств букв (простые множества): | Решение для множеств треугольников(сложные множества): |
| …Ответ на п. 3 задания 1: B\A={т} | …Ответ на п. 3 задания 1: B\A - множество непрямоугольных равнобедренных треугольников. |
| На рис. 1 X3= B\A показано в виде правого полумесяца с вертикальной штриховкой. |
Решение.
4) Найдем разность X= АÈВ. Данное задание - на операции над простыми и сложными множествами.
| ОПЕРАЦИЯ ОБЪЕДИНЕНИЯ МНОЖЕСТВ. КРАТКАЯ ТЕОРИЯ. Определение. Объединением (или суммой) множеств А и В называется множество С, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В. Обозначается: С = АÈВ (или С = А + В). Знак «È» называется знаком объединения. На рис. 1 изображены два множества точек плоскости: круг А и круг В. Их объединение С = АÈВ — это область, покрытая или горизонтальной, или вертикальной, или наклонной штриховкой. КОНЕЦ ТЕОРИИ. | |
| Согласно определения C=АÈВ. имеем… | |
| Решение для множеств букв (простые множества): | Решение для множеств треугольников(сложные множества): |
| …Ответ на п. 4 задания 1: AÈB={и,с,а,л,т} | …Ответ на п. 4 задания 1: AÈB - множество прямоугольных равнобедренных треугольников, множество прямоугольных неравнобедренных треугольников и множество непрямоугольных равнобедренных треугольников. |
| На рис. 1 три множества: в виде левого и правого полумесяцев, а также в виде двойного кругового сегмента,- соответственно с наклонной, вертикальной и горизонтальной штриховками. |
Решение.
5) Найдем разность X5= АÈВ. Данное задание - на операции над простыми и сложными множествами.
ОПЕРАЦИЯ ДОПОЛНЕНИЯ МНОЖЕСТВА. КРАТКАЯ ТЕОРИЯ. Определение. Дополнением множества А до множества U называется разность C=U\A. Само универсальное множество U, изображают в виде прямоугольника, а его подмножества — в виде кругов, расположенных внутри прямоугольника. Дополнение некоторого множества А до универсального множества U обозначается ┐A или 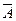 . Дополнение множества А (до U), т.е. множество ┐A изображается той частью прямоугольника, которая лежит за пределами круга, изображающего А (рис. 1, a). . Дополнение множества А (до U), т.е. множество ┐A изображается той частью прямоугольника, которая лежит за пределами круга, изображающего А (рис. 1, a). | |
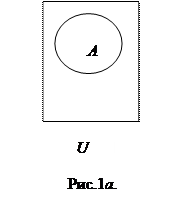 КОНЕЦ ТЕОРИИ. КОНЕЦ ТЕОРИИ. | |
| Согласно определения C= ┐A =U\A. имеем… | |
| Решение для множеств букв (простые множества): | Решение для множеств треугольников(сложные множества): |
| …Ответ на п. 5 задания 1: ┐A – множество всех русских букв, кроме “л”,”и”,”с”,”а” | …Ответ на п. 5 задания 1: ┐A - множество непрямоугольных треугольников. |
| …Ответ на п. 6 задания 1: ┐B – множество всех русских букв, кроме ”а”, ”и”,”с”,“т” | …Ответ на п. 6 задания 1: ┐B - множество неравнобедренных треугольников. |
| Ответ: Множества А и В находятся вотношениипересечения, что видно из пересечения кругов А и В на рис. 1. | Ответ: Множества А и В находятся вотношениипересечения, что видно из пересечения кругов А и В на рис. 1. |
ЗАНЯТИЕ 2.
Решение.
Пусть даны конечные множества элементов A и B с числом элементов соответственно k1=n(A) и k2=n(B). Тогда могут быть определены множества X= AÈ B, X1= AÇB, X2= A\B, X3= B\A с числом элементов соответственно k3=n(AÈB), k4=n(AÇB), k5=n(A\ B), k6=n(B \A).Вэтомслучае справедливо правило суммы (ф. (1)), два следствия из него (ф. (2-3)), а также контрольное соотношение (ф. (4)):
1) n(AÇB)= n(A)+n(B)-n(AÈB), k4= k1+ k2- k3, (1)
2) n(A\B)= n(A)-n(AÇB), k5= k1- k4, (2)
3) n(B\A)= n(B)-n(AÇB), k6= k2- k4, (3)
4) n(AÈB)= n(A\B)+n(B\A)+n(AÇB), k3= k5+ k6+ k4. (4)
КОНЕЦ ТЕОРИИ.
Обозначим через A и B множества студентов группы, факультативно изучавших соответственно математику и информатику с числом элементов, согласно условия, соответственно k1=n(A)=13 и k2=n(B)=11. Тогда по определению операции объединения множеств X= AÈB - множество студентов группы, факультативно изучавших математику и/или информатику. Число его элементов, согласно условия, равно k3=n(AÈB)=18.
1) По определению операции пересечения множеств X= AÇB - множество студентов группы, факультативно изучавших математику и информатику одновременно. Число элементов этого множества, обозначенное через k4=n(AÇB), является искомым в пункте 1 вопроса задания. Его мы найдем, по ф.(1) правила суммы (см. краткую теорию). Имеем
n(AÇB)= n(A)+n(B)-n(AÈB), k4= k1+ k2- k3, n(AÇB)= k4=13+11-18=6.
Ответ: n(AÇB)= 6, т. е. 6 студентов группы факультативно изучали математику и информатику одновременно.
2) По определению операции вычитания множеств X2= A\B - множество студентов группы, факультативно изучавших только математику, но не информатику. Число элементов этого множества, обозначенное через k5=n(A\B), является искомым в пункте 2 вопроса задания. Его мы найдем, по ф.(2) следствия правила суммы (см. краткую теорию). Имеем
n(A\B)= n(A)-n(AÇB), k5= k1 - k4, n(A\B)= k5=13-6=7.
Ответ: n(A\B)= 7, т. е. 7 студентов группы факультативно изучали только математику, но не информатику.
3) По определению операции вычитания множеств X3= B\A - множество студентов группы, факультативно изучавших только информатику, но не математику. Число элементов этого множества, обозначенное через k6=n(B\A), является искомым в пункте 3 вопроса задания. Его мы найдем, по ф.(3) следствия правила суммы (см. краткую теорию). Имеем
n(B\A)= n(B)-n(AÇB), k6= k2 - k4, n(B\A)= k6=11-6=5.
Ответ: n(B\A)= 5, т. е. 5 студентов группы факультативно изучали только информатику, но не математику.
4) По ф.(4) контрольного соотношения (см. краткую теорию) имеем
n(AÈB)= n(A\B)+n(B\A)+n(AÇB), k3= k5+ k6+ k4, 18=7+5+6=18.
Итак, 18=18. Задание решена верно.
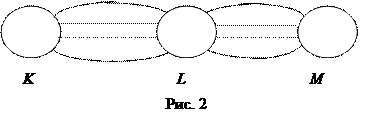
Задание 3. Из пункта K (см. рис. 2) в пункт L ведут k1=n(A)=13 непересекающихся дорог, а из пункта L в пункт M - k2=n(B)=11 дорог. Сколько существует способов проезда из пункта K в пункт M через пункт L?
ПРАВИЛО ПРОИЗВЕДЕНИЯ. КРАТКАЯ ТЕОРИЯ.
Пусть даны конечные множества элементов A={a1, a2,…, ar} и B={b1, b2,…, bs} с числом элементов соответственно r=n(A) и s=n(B). Тогда может быть определено множество X= =AÄB, называемое декартовым произведением множеств A и B в указанном порядке:
X= =AÄB=
| {(a1, b1), | (a1,b2) | … | (a1, bs) |
| (a2, b1), | (a2,b2) | … | (a2, bs) |
| … | … | … | … |
| (ar, b1), | (ar,b2) | … | (ar, bs)}. |
Очевидно, в каждой клетке последней прямоугольной таблицы по одной паре элементов множеств A и B, являющиеся, в свою очередь, отдельными элементами множества X= =AÄB (декартовым произведением множеств A и B). Число элементов последнего множества X=AÄB, которое мы обозначим n(X)= n(AÄB) равно числу клеток в последней прямоугольной таблицы размера r строк ´ s столбцов = r s =n(A) n(B). Итак, мы доказали правило произведения:
n(AÄB)= n(A) n(B). (5)
КОНЕЦ ТЕОРИИ.
Решение.
Обозначим через A={a1, a2,…, ar} и B={b1, b2,…, bs} множества непересекающихся дорог, ведущих соответственно из пункта K в пункт L и из пункта L в пункт M (см. рис. 2). Ихчисло элементов, согласно условия, равны соответственно r=n(A)=13 и s=n(B)=11.
Составление маршрутов проезда из пункта K в пункт M через пункт L есть по сути составление элементов декартова произведения множеств A и B в указанном порядке. Например, элемент (a1, b1) декартова произведения соответствует тому, что из пункта K в пункт L выбрана первая дорога a1 из списка всех дорог, а из пункта L в пункт M выбрана тоже первая дорога b1 из списка всех дорог и т. д. Наконец, элемент (ar, bs).декартова произведения соответствует тому, что из пункта K в пункт L выбрана последняя дорога arиз списка всех дорог, а из пункта L в пункт M выбрана тоже последняя дорога bsиз списка всех дорог.
Поэтому искомое число маршрутов проезда из пункта K в пункт M через пункт L есть общее число элементов декартова произведения множеств A и B, то есть равно, согласно правила произведения, n(AÄB)= n(A) n(B)= r × s =13×11 =143.
Ответ: n(AÄB)=143, т. е. 143 различных маршрутов проезда из пункта K в пункт M через пункт L.
ЗАНЯТИЕ 3.
Таблица. Значения факториалов первых натуральных чисел и нуля.
| n= | |||||||||||
| n!= |
КОНЕЦ ТЕОРИИ.
Решение.
В задании 4n=5, ибо переставляются местами всевозможными способами n=5 штук различных цифр: 1,3,5,7,9. При этом каждой новой перестановке цифр соответствует новый телефонный номер (натуральное число). Поэтому искомое число различных телефонных номеров равно числу различных перестановок без повторений из n=5 штук различных элементов.
Согласно теории, искомое число равно Р5 = 5!= 120 различных 5– значных телефонных номеров.
Ответ: 120 различных 5– значных телефонных номеров.
Задание 5 (начисло перестановок с повторениями.)
Сколько различных n– значных телефонных номеров (натуральных чисел) можно написать, переставляя следующий набор n штук цифр: 1,1,1,3,3,5?
ЧИСЛО ПЕРЕСТАНОВОК С ПОВТОРЕНИЯМИ.КРАТКАЯ ТЕОРИЯ
Перестановки с повторениями
Перестановками с повторениями из т элементов n различных типов, среди которых k1одинаковых элементов 1-го типа, k2одинаковых элементов 2-го типа, ... , knодинаковых элементов п-го типа (k1 + k2 + ... + kп = m) , называются их последовательности, отличающиеся только порядком входящих в них элементов.
Пример. Перестановки из 3 элементов, среди которых 2 одинаковых элемента типа а и 1 элемент типа b: ааb, аbа, bаа.
Число перестановок из т элементов, среди которых k1- одинаковых элементов 1-го типа, k2 одинаковых элементов2-го типа,..., kп- одинаковых элементов n-го типа [обозначается Р (m; k1,k2 ,..., kп) ] равно:
Р (m; k1,k2 ,..., kп)= т!/ (k1!k2 !... kп!).
Для примера перестановок с повторениями из 3 элементов, среди которых 2 одинаковых типа а и 1 элемент типа b, имеем Р (m=3; k1=2,k2=1)= 3!/ (2!1!).
КОНЕЦ ТЕОРИИ.
Решение.
В задание 5m=6, ибо переставляются местами всевозможными способами m =6 штук различных цифр: 1,1,1,3,3,5, среди которых есть повторяющиеся (одинаковые). При этом каждой новой перестановке цифр соответствует новый телефонный номер (натуральное число). Поэтому искомое число различных телефонных номеров равно числу различных перестановок с повторениями из m =6 штук элементов, среди которых k1=3 одинаковых элементов 1-го типа (цифра 1), k2=2 одинаковых элементов2-го типа (цифра 3), k3=1одинаковых элементов 3-го типа (цифра 5), равно Р (m; k1,k2 ,..., kп)= т!/ (k1!k2 !... kп!), Р(6; 3, 2, 1) = 6!/(3! 2! 1!)= =60.
Ответ: Р(6; 3, 2, 1) = 60, т. е 60 различных вариантов 6– значных телефонных номеров (6-значных чисел), содержащих цифру 1 трижды, 3 —дважды и 5 — один раз.
Задание 6 (на число неупорядоченных разбиений с фиксированными размерами частей).
Сколько всего вариантов можно получить, разбивая группу из пяти человек (из пяти солдат) на три подгруппы — две подгруппы по два человека (по два автоматчики) и одна подгруппа из одного человека (из одного пулеметчика)?
НЕУПОРЯДОЧЕННЫЕ РАЗБИЕНИЯ. КРАТКАЯ ТЕОРИЯ
Неупорядоченное разбиениеn -элементного множества X — это любое семейство {X1, X2,…, Xk}, где 1≤k≤п; X1, X2,…, Xk - непустые попарно непересекающиеся подмножества множества X , объединение которых равноX.
Называем такое разбиение неупорядоченным, таккак семейство — это неупорядоченнаясовокупность.
Пример.Для множества {а,b,с} неупорядоченное разбиение это, например, {{а},{b,с}}. Причем {{а},{b,с}}={{b,с},{а}}.
Для множества с п элементами обозначим через D(n; k1, k2,…, kn) число всех таких неупорядоченных разбиений,в которых есть k1 подмножеств с однимэлементом, k2 подмножеств с двумяэлементами и т.д., где k1≥0, k2≥0,…, kn≥0; k1+2 k2+…+n kn= n.
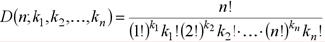 Имеем
Имеем
КОНЕЦ ТЕОРИИ.
Решение.
Каждый вариант— это неупорядоченное разбиение { Иванов, Петров, Сидоров, Андреев, Борисов }. Множество из 5 элементов Один из вариантов разбиения {{Иванов, Петров}, {Сидоров, Андреев}, {Борисов}}
Имеем п = 5, k1=1, k2=2, k3=0, k4=0, k5=0 (так как по условию нет подгрупп из трех, четырех, пяти человек).
Получим

Ответ: 15 вариантов.
Задание 7 (начисло упорядоченных разбиений с фиксированными размерами частей).
Сколькими способами можно выбрать из десяти солдат трех пулеметчиков, трех гранатометчиков и четырех автоматчиков (3 пулеметчика 3 гранатометчика 4 автоматчика, всего 10 солдат)?
УПОРЯДОЧЕННЫЕ РАЗБИЕНИЯ.КРАТКАЯ ТЕОРИЯ
Упорядоченным разбиениемконечного множества X с n элементами называется любой кортеж вида <X1, X2,…, Xk>, где 1 ≤k ≤n; X1, X2,…, Xk - непустые попарно непересекающиеся, подмножества множества X, объединение которых равно X.
Называем такое разбиение упорядоченным, так как элементы кортежа упорядочены.
Пример.Для множества {а,b,с} упорядоченное разбиениеэто, например, кортеж <{{а},{b,с}}>.Причем <{{а},{b,с}}>¹<{{b,с},{а}}>.
Для множества с п элементами обозначим через E(n; m1, m2,…, mk,) число всех таких упорядоченных разбиений на подмножества X1, X2,…, Xk, содержащие m1, m2,…, mk, где m 1≥0, m 2≥0,…, m k≥0; m 1+ m 2+…+ m k= n.
Число всех упорядоченных разбиений<X1, X2,…, Xk> множества с п элементами на подмножества X1, X2,…, Xk, содержащие m1, m2,…, mk, элементов соответственно. определяется по полиномиальной формуле 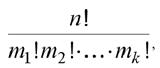
где m1≥1, m2≥1,…, mn≥1; m1+ m2+…+mk= n.
КОНЕЦ ТЕОРИИ.
Решение.
В задании имеем упорядоченное разбиение <X1, X2, X3>множества с десятьюэлементами, где X1 - подмножество пулеметчиков,Х2 — подмножество гранатометчиков,Х3 — подмножество автоматчиков;
поэтому п = 10, m1 = 3, т2, = 3, т3 = 4.
Тогда всего есть
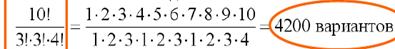
Ответ: 4200 вариантов
ЗАНЯТИЕ 4.
Решение.
В задании 8m=3, n=5. Тогда по формуле имеем 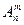 = n!/(n-m)!. Подставляя в формулу m=3 и n=5, имеем
= n!/(n-m)!. Подставляя в формулу m=3 и n=5, имеем 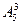 = 5!/(5-3)!= 5!/ 2!=120/2=60.
= 5!/(5-3)!= 5!/ 2!=120/2=60.
Ответ: 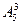 =60, т. е 60 различных вариантов 3– значных телефонных номеров (3-значных чисел) можно написать, выбирая цифры с перестановкой без возможности повторения из следующего набора n=5 штук разных цифр: 1,3,5,7,9.
=60, т. е 60 различных вариантов 3– значных телефонных номеров (3-значных чисел) можно написать, выбирая цифры с перестановкой без возможности повторения из следующего набора n=5 штук разных цифр: 1,3,5,7,9.
Задание 9(начисло размещений с возможными повторениями).
Сколько различных m– значных телефонных номеров (натуральных чисел) можно написать, выбирая цифры с перестановкой и с возможностью повторения из следующего набора n=5 штук разных цифр: 1,3,5,7,9? Решить задание для m=3.
ЧИСЛО РАЗМЕЩЕНИЙ С ПОВТОРЕНИЯМИ.КРАТКАЯ ТЕОРИЯ
Размещениями с повторениями элементов n различных типов по т называются их последовательности из т элементов, отличающиеся друг от друга самими элементами или их порядком. При этом возможно и т≤ n, и т>n, поскольку допускается повторение элементов в последовательности из т элементов.
Число всех возможных размещений из га различных элементов по т (обозначается 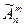 )есть
)есть 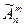 = nm.
= nm.
КОНЕЦ ТЕОРИИ.
Решение.
В задании 9m=3, n=5. Тогда по формуле имеем 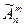 = nm. Подставляя в формулу m=3 и n=5, имеем
= nm. Подставляя в формулу m=3 и n=5, имеем 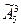 = 53=125.
= 53=125.
Ответ: 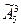 =125., т. е 125 различных вариантов 3– значных телефонных номеров (3-значных чисел) можно написать, выбирая цифры с перестановкой с возможностью повторения из следующего набора n=5 штук разных цифр: 1,3,5,7,9.
=125., т. е 125 различных вариантов 3– значных телефонных номеров (3-значных чисел) можно написать, выбирая цифры с перестановкой с возможностью повторения из следующего набора n=5 штук разных цифр: 1,3,5,7,9.
Задание 10(начисло размещений с обязательными повторениями).
Сколько различных m– значных телефонных номеров (натуральных чисел) можно написать, выбирая цифры с перестановкой и с обязательным их повторением в номере из следующего набора n=5 штук разных цифр: 1,3,5,7,9? Решить задание для m=3.
ЧИСЛО РАЗМЕЩЕНИЙ С ОБЯЗАТЕЛЬНЫМИ ПОВТОРЕНИЯМИ.КРАТКАЯ ТЕОРИЯ
Пусть A - множество размещений элементов с возможными их повторениями из n по m элементов, B - множество размещений элементов без возможности их повторениями из n по m элементов. Очевидно, число элементов n(A) множества A равно 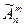 , а числоэлементов n(B) множества B равно
, а числоэлементов n(B) множества B равно 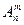 . Так как множество B есть подмножество множества A, то BÌA, поэтому число элементов их пересечения равно n(A∩B)=n(B)=
. Так как множество B есть подмножество множества A, то BÌA, поэтому число элементов их пересечения равно n(A∩B)=n(B)= 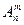 . Наконец, пусть A\B - множество размещений элементов с обязательными повторениями из n по m элементов. Тогда по следствию из правила суммы число элементов последнего множества A\B равно n(A\B)= =n(A)-n(A∩B)=
. Наконец, пусть A\B - множество размещений элементов с обязательными повторениями из n по m элементов. Тогда по следствию из правила суммы число элементов последнего множества A\B равно n(A\B)= =n(A)-n(A∩B)= 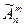 -
- 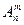 .
.
КОНЕЦ ТЕОРИИ.
РЕШЕНИЕ.
В задании 10m=3, n=5. Тогда по формуле имеем n(A\B)= 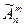 -
- 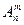 =
= 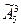 -
- 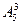 =125-60=65.
=125-60=65.
Ответ: n(A\B)= 65, т. е 65 различных вариантов 3– значных телефонных номеров (3-значных чисел) можно написать, выбирая цифры с перестановкой с обязательным повторением из следующего набора n=5 штук разных цифр: 1,3,5,7,9.
ЗАНЯТИЕ 5.
Решение.
В задании 11m=3, n=5. Тогда по формуле имеем 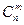 = n!/(m!(n-m)!). Подставляя в формулу m=3 и n=5, имеем
= n!/(m!(n-m)!). Подставляя в формулу m=3 и n=5, имеем 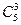 = 5!/(3)!(5-3)!)= 5!/((3)!2!)=120/(6×2)=10.
= 5!/(3)!(5-3)!)= 5!/((3)!2!)=120/(6×2)=10.
Ответ: 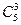 =10, т. е 10 различных подарков по m=3 различных предметов в каждом можно составить, выбирая предметы без повторения из следующего набора n=5 предметов
=10, т. е 10 различных подарков по m=3 различных предметов в каждом можно составить, выбирая предметы без повторения из следующего набора n=5 предметов
Задание 12(начисло сочетаний с возможными повторениями).
Сколько различных подарков по m предметов в каждом можно составить, выбирая предметы с возможностью повторения из следующего набора n=5 штук разных предметов: 1-яблоко,3 - слива, 5 - груша, 7 - апельсин, 9 - банан? Решить задание для m=3.
ЧИСЛО СОЧЕТАНИЙ С ВОЗМОЖНЫМИ ПОВТОРЕНИЯМИ.КРАТКАЯ ТЕОРИЯ
Сочетаниями с повторениями элементов n различных типов по т называются их неупорядоченные наборы из т элементов, отличающиеся друг от друга только самими элементами.
При этом возможно и т ≤ п, и т > п,поскольку допускается повторение элементов в их неупорядоченном наборе из т элементов.
Число всех сочетаний с повторениями элементов л различных типов по неупорядоченным наборам из т элементов (обозначается 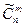 ) есть
) есть 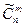 =
= 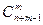 =
= 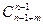 .
.
КОНЕЦ ТЕОРИИ.
Решение.
В задании 12m=3, n=5. Тогда по формуле имеем 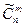 =
= 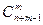 =(n+m-1)!/(m!(n-1)!). Подставляя в формулу m=3 и n=5, имеем
=(n+m-1)!/(m!(n-1)!). Подставляя в формулу m=3 и n=5, имеем 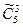 =(5+3-1)!/(3! (5-1)!)==7!/((3)!4!)=5040/(6×24)= 35.
=(5+3-1)!/(3! (5-1)!)==7!/((3)!4!)=5040/(6×24)= 35.
Ответ: 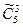 =35, т. е. 35 различных подарков по m=3 предмета в каждом можно составить, выбирая предметы с возможностью повторения из набора n=5 штук разных предметов.
=35, т. е. 35 различных подарков по m=3 предмета в каждом можно составить, выбирая предметы с возможностью повторения из набора n=5 штук разных предметов.
Задание 13(начисло сочетаний с обязательными повторениями).
Сколько различных подарков по m предметов в каждом можно составить, выбирая предметы с обязательными повторениями из следующего набора n=5 штук разных предметов: 1-яблоко,3 - слива, 5 - груша, 7 - апельсин, 9 - банан? Решить задание для m=3.
ЧИСЛО СОЧЕТАНИЙ С ОБЯЗАТЕЛЬНЫМИ ПОВТОРЕНИЯМИ.КРАТКАЯ ТЕОРИЯ
Пусть A - множество сочетаний элементов с возможными их повторениями из n по m элементов, B - множество сочетаний элементов без возможности их повторениями из n по m элементов. Очевидно, число элементов n(A) множества A равно 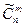 , а числоэлементов n(B) множества B равно
, а числоэлементов n(B) множества B равно 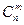 . Так как множество B есть подмножество множества A, то BÌA, поэтому число элементов их пересечения равно n(A∩B)=n(B)=
. Так как множество B есть подмножество множества A, то BÌA, поэтому число элементов их пересечения равно n(A∩B)=n(B)= 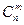 . Наконец, пусть A\B - множество сочетаний элементов с обязательными повторениями из n по m элементов. Тогда по следствию из правила суммы число элементов последнего множества A\B равно n(A\B)= =n(A)-n(A∩B)=
. Наконец, пусть A\B - множество сочетаний элементов с обязательными повторениями из n по m элементов. Тогда по следствию из правила суммы число элементов последнего множества A\B равно n(A\B)= =n(A)-n(A∩B)= 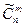 -
- 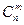 .
.
КОНЕЦ ТЕОРИИ.
РЕШЕНИЕ.
В задании 13m=3, n=5. Тогда по формуле имеем n(A\B)= 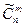 -
- 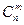 =
= 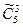 -
- 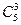 =35-10=25.
=35-10=25.
Ответ: n(A\B)= 25, т. е 25 различных подарков по m=3 предметов в каждом можно составить, выбирая предметы с обязательным повторением из набора n=5 штук разных предметов.
ЗАНЯТИЕ 6.
РАЗМЕЩЕНИЯ И СОЧЕТАНИЯ БЕЗ ПОВТОРЕНИЙ И С ПОВТОРЕНИЯМИ НА ПРИМЕРЕ БРОСАНИЯ ИГРАЛЬНЫХ КОСТЕЙ.
Цель: Изучить на практике методику вычисления количества размещений и сочетаний без повторений и с повторениями на примере бросания игральных костей
.Содержание:
Задание 14 (на число размещений и сочетаний на примере бросания игральных костей).
Задание 14 (на число размещений и сочетаний на примере бросания игральных костей).
Брошены наудачу m штук правильных n-гранников, на каждой грани которых нанесены точками последовательные натуральные числа от 1 до n (игральные “кубики”) (см. параграф ”Тела Платона”). Сколько при этом возможно результатов бросания в следующих случаях:
1) все m штук правильных n-гранников разные (например разного цвета), а учитываются только разные (неодинаковые, неповторяющиеся) числа, выпавшие на них,
2) все m штук правильных n-гранников разные (например разного цвета), а учитываются только в том числе и одинаковые (повторяющиеся) числа, выпавшие на них,
3) все m штук правильных n-гранников разные (например разного цвета), а учитываются обязательно одинаковые (повторяющиеся) числа, выпавшие на них,
4) все m штук правильных n-гранников одинаковые, а учитываются только разные (неодинаковые, неповторяющиеся) числа, выпавшие на них,
5) все m штук правильных n-гранников одинаковые, а учитываются только в том числе и одинаковые (повторяющиеся) числа, выпавшие на них,
6) все m штук правильных n-гранников одинаковые, а учитываются обязательно одинаковые (повторяющиеся) числа, выпавшие на них?
Замечание.В качестве правильных n-гранников в этом задании могут быть выбраны любые из 5 тел Платона, показанные на рис. 3 (n=4 - тетраэдр, n=6 – гексаэдр или куб, n=8 - октаэдр, n=12 - додекаэдр, n=20 - икосаэдр). Решить задание например для n=6 и m=2.
Решение
Данное задание - на число размещений и сочетаний на примере бросания игральных костей.Ее решение дано в виде таблицы ниже:
| Тип учитываемых чисел¯ | Тип используемых n-гранников ¯ | |
| Все разные | Все одинаковы | |
| Все разные=запрещеныодинаковые | 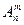 решает п. 1 задания 14 решает п. 1 задания 14 | 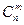 решает п. 4 задания 14 решает п. 4 задания 14 |
| Возможны одинаковые | 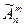 решает п. 2 задания 14 решает п. 2 задания 14 | 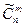 решает п. 5 задания 14 решает п. 5 задания 14 |
| Обязательно есть одинаковые | 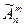 - - 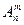 решает п. 3 задания 14 решает п. 3 задания 14 |
