Комплексное сопротивление последовательного контура
Последовательный колебательный контур можно представить в виде четырехполюсника, выходное напряжение которого снимается либо с индуктивности (рис. 11.3, а), либо с ёмкости (рис. 11.3, б).

а) б)
Рис. 11.3
Определим комплексное входное сопротивление последовательного контура в режиме холостого хода на выходе с учётом соотношений для резонансной частоты  и добротности
и добротности  ,
,


где
 ,
, 
— модуль и аргумент комплексного входного сопротивления контура.
На рис. 11.4 показаны векторные диаграммы тока и напряжений на элементах контура для трёх соотношений частоты входного напряжения и резонансной частоты контура:  (резонанс) (рис. 11.4, а),
(резонанс) (рис. 11.4, а),  (рис. 11.4, б) и
(рис. 11.4, б) и  (рис. 11.4, в).
(рис. 11.4, в).

а) б) в)
Рис. 11.4
 Входные частотные характеристики
Входные частотные характеристики  ,
,  , построенные в координатах
, построенные в координатах  и
и  , неудобны для сравнительного анализа колебательных контуров, имеющих разные параметры элементов, поскольку области характеристик, соответствующие резонансу и представляющие наибольший интерес, оказываются сдвинутыми относительно друг друга по осям координат. Поэтому на практике обычно используют нормированные характеристики. Нормирование обычно осуществляется путем деления исследуемой величины на её некоторое характерное значение, которое называется нормирующим значением.
, неудобны для сравнительного анализа колебательных контуров, имеющих разные параметры элементов, поскольку области характеристик, соответствующие резонансу и представляющие наибольший интерес, оказываются сдвинутыми относительно друг друга по осям координат. Поэтому на практике обычно используют нормированные характеристики. Нормирование обычно осуществляется путем деления исследуемой величины на её некоторое характерное значение, которое называется нормирующим значением.
При нормировании модуля входного сопротивления  в качестве нормирующего значения будем использовать сопротивление потерь
в качестве нормирующего значения будем использовать сопротивление потерь 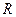 , а при нормировании частоты — резонансную частоту
, а при нормировании частоты — резонансную частоту  . Тогда нормированный модуль сопротивления комплексного входного сопротивления последовательного контура будет иметь
. Тогда нормированный модуль сопротивления комплексного входного сопротивления последовательного контура будет иметь
 ,где
,где  — нормированная частота.
— нормированная частота.
Нормированные частотные зависимости модуля и аргумента комплексного входного сопротивления контура показаны на рис. 11.5. В результате, области частотных характеристик, соответствующие резонансу, находятся в окрестности одной и той же точки с координатами  ,
,  , при любых значениях параметров элементов контура, что упрощает анализ частотных характеристик контуров, имеющих разные параметры.
, при любых значениях параметров элементов контура, что упрощает анализ частотных характеристик контуров, имеющих разные параметры.
Из частотных характеристик (рис. 11.5) видно, что увеличение добротности контура Q вызывает сужается диапазон частот, в котором происходит наиболее резкое изменение модуля и аргумента входного сопротивления. На частоте ниже резонансной сопротивление контура носит резистивно-емкостной характер, и его аргумент отрицателен  , а на частоте выше резонансной сопротивление контура носит резистивно-индуктивный характер и его аргумент положителен
, а на частоте выше резонансной сопротивление контура носит резистивно-индуктивный характер и его аргумент положителен  (рис.11.5, б).
(рис.11.5, б).
Определим нормированное комплексное действующее значение тока контура, используя в качестве нормирующего значения резонансный ток  ,
,
 ,
,
где  и
и  — модуль и аргумент нормированного тока.
— модуль и аргумент нормированного тока.
На рис. 11.6 показаны частотные зависимости модуля комплексного тока трёх контуров с различными частотами настройки и различными добротностями.

Рис. 11.6
Максимумы частотных характеристик, нормированных только по частоте (рис. 11.6, а), расположены на одной нормированной частоте  , но отличаются по уровню. Частотные характеристики (рис. 11.6, б), нормирование по частоте и по уровню, обеспечивает совпадение расположения максимумов характеристик не только по частоте, но и по уровню. Видно, что, чем выше добротность контура
, но отличаются по уровню. Частотные характеристики (рис. 11.6, б), нормирование по частоте и по уровню, обеспечивает совпадение расположения максимумов характеристик не только по частоте, но и по уровню. Видно, что, чем выше добротность контура  , тем острее характеристика в окрестность резонансной частоты и лучше её частотная избирательность.
, тем острее характеристика в окрестность резонансной частоты и лучше её частотная избирательность.
Лекция № 13
