Энергетические соотношения в последовательном контуре
Определим резонансные напряжения на индуктивности ёмкости контура:
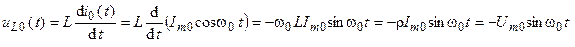 ;
;
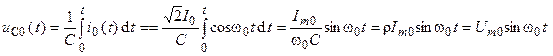 ,
,
где 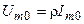 — амплитуда напряжения ёмкости и индуктивно на резонансной частоте.
— амплитуда напряжения ёмкости и индуктивно на резонансной частоте.
Из полученных выражений видно, что при резонансе напряжения реактивных элементов контура равны по амплитуде и противоположны по фазе 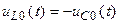 .
.
Определим мгновенные значения энергии, запасаемой в реактивных элементах контура в произвольный момент времени:
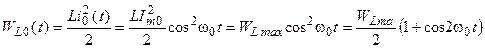
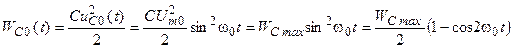 ,
,
где 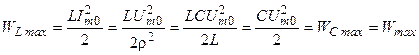 — максимальная энергия, запасаемая в реактивных элементах контура.
— максимальная энергия, запасаемая в реактивных элементах контура.
Таким образом, при резонансе значения энергии, запасаемые реактивными элементами контура, содержат одинаковые постоянные составляющие и равные по амплитуде, но противоположные по фазе гармонические составляющие, изменяющиеся с удвоенной частотой 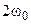 .
.
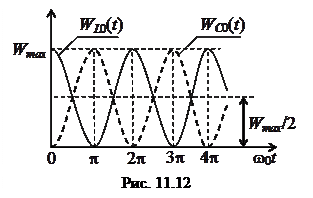 Временные диаграммы мгновенных значений энергии, запасаемых реактивными элементами контура, изображены на рис. 11.2.
Временные диаграммы мгновенных значений энергии, запасаемых реактивными элементами контура, изображены на рис. 11.2.
Из временных диаграмм видно, что при резонансе происходит непрерывной обмен энергией между индуктивностью и ёмкостью контура. При этом алгебраическая сумма энергий, запасаемых реактивными элементами контура, в любой момент времени остаётся постоянной и равной некоторому постоянному значению
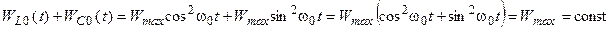 .
.
Определим мгновенные мощности реактивных элементов контура
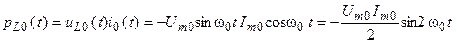 ;
;
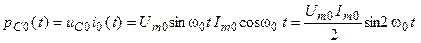 .
.
Из полученных выражений следует, что мгновенные мощности реактивных элементов изменяются по гармоническому закону с удвоенной резонансной частотой, имеют одинаковые амплитуды и противофазны. Поэтому алгебраическая сумма этих мощностей в любой момент времени равна нулю, что свидетельствует о реактивном характере этих мощностей.
Определим среднюю мощность потерь, выделяемую при резонансе в сопротивлении 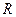 за один период колебаний,
за один период колебаний,
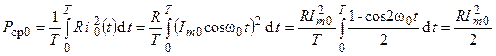 .
.
Добротностью последовательного колебательного контура называется отношение амплитуды напряжения на реактивном элементе контура к амплитуде входного напряжения контура при резонансе
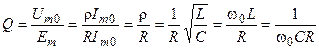 .
.
Найденную величину часто называют собственной добротностью последовательного контура, поскольку она определяется без учёта влияния внутреннего сопротивления источника напряжения и сопротивления нагрузки.
Резонансное сопротивление контура можно выразить через добротность и характеристическое сопротивление 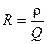 . Видно, что резонансное сопротивление последовательного контура меньше характеристическое сопротивление в число раз, равное добротности контура.
. Видно, что резонансное сопротивление последовательного контура меньше характеристическое сопротивление в число раз, равное добротности контура.
Величина, обратная добротности контура, называется затуханием 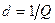 .
.
Выразим добротность контура через энергетические параметры резонансного режима роботы контура
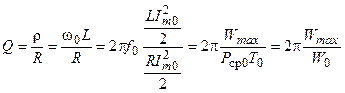 ,
,
где 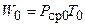 — энергия потерь за период
— энергия потерь за период 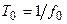 колебаний в сопротивлении
колебаний в сопротивлении 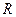 .
.
С энергетической точки зрения добротность пропорциональна отношению максимального значения энергии, запасаемой в реактивных элементах, к энергии потерь за один период колебаний. Поскольку у реальных колебательных LC-контуров 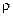 составляет в среднем сотни ом, а
составляет в среднем сотни ом, а 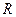 ь — от долей ома до нескольких ом, то добротность контуров достигает 100-300.
ь — от долей ома до нескольких ом, то добротность контуров достигает 100-300.
Если LC-контур отключить от источника напряжения, замкнув накоротко его выводы, то колебательный процесс продолжится до тех пор, пока вся энергия, запасенная в реактивных элементах контура, не будет израсходована в виде энергии потерь. Чем больше добротность контура, тем меньше затухание и дольше длится колебательный процесс.
