Согласование нагрузки с источником энергии
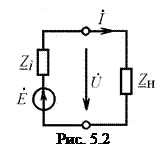
Рассмотрим электрическую цепь, состоящую из источника энергии и нагрузки.
Пусть источник энергии представлен последовательной схемой замещения (рис 5.2), причем его внутреннее сопротивление имеет комплексный характер: 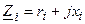 . Задача согласования нагрузки с источником энергии заключается в выборе такого сопротивления нагрузки
. Задача согласования нагрузки с источником энергии заключается в выборе такого сопротивления нагрузки 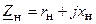 , при котором в цепи будут выполняться требуемый критерий согласования.
, при котором в цепи будут выполняться требуемый критерий согласования.
 Первый критерий согласования источника с нагрузкой заключается в обеспечении максимума активной мощности, передаваемой в нагрузку. Активная мощность нагрузки
Первый критерий согласования источника с нагрузкой заключается в обеспечении максимума активной мощности, передаваемой в нагрузку. Активная мощность нагрузки
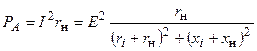 .
.
Отсюда видно, что 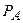 является функцией двух переменных:
является функцией двух переменных: 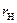 и
и 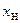 . В связи с тем, что вещественная и мнимая составляющая сопротивления нагрузки не зависят одна от другой, выбор значения каждой из этих величин соответствующего максимуму
. В связи с тем, что вещественная и мнимая составляющая сопротивления нагрузки не зависят одна от другой, выбор значения каждой из этих величин соответствующего максимуму 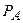 , можно производить в отдельности. Величина
, можно производить в отдельности. Величина 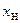 входит только в знаменатель выражения для активной мощности. Очевидно, что максимальное значение
входит только в знаменатель выражения для активной мощности. Очевидно, что максимальное значение 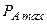 по этой переменной будет достигнуто, если
по этой переменной будет достигнуто, если 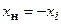 . При этом
. При этом 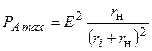 .
.
Для определения значения 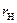 , соответствующего наибольшему возможному значению (максимум-максиморум) активной мощности нагрузки
, соответствующего наибольшему возможному значению (максимум-максиморум) активной мощности нагрузки 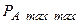 , продифференцируем
, продифференцируем 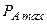 по
по 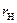 и приравняем к нулю полученное выражение
и приравняем к нулю полученное выражение
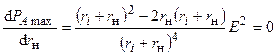 , или
, или 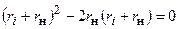 .
.
Решая уравнение, находим условие 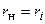 , при котором этом активная мощность достигает максимально возможного значения (рис. 5.3, а)
, при котором этом активная мощность достигает максимально возможного значения (рис. 5.3, а)
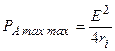 .
.
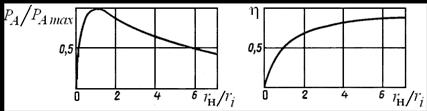
а) б)
Рис. 5.3
Объединяя полученные условия, находим, что максимально возможное значение активной мощности нагрузки 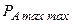 соответствует
соответствует 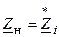 , то есть сопротивление нагрузки должно быть равно сопротивлению, комплексно сопряженному с внутренним сопротивлением источника.
, то есть сопротивление нагрузки должно быть равно сопротивлению, комплексно сопряженному с внутренним сопротивлением источника.
В частном случае, если внутреннее сопротивление источника имеет резистивный характер ( 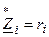 ), то для согласования источника энергии с нагрузкой по критерию наибольшей активной мощности, передаваемой в нагрузку, сопротивление нагрузки должно быть равно внутреннему сопротивлению источника.
), то для согласования источника энергии с нагрузкой по критерию наибольшей активной мощности, передаваемой в нагрузку, сопротивление нагрузки должно быть равно внутреннему сопротивлению источника.
Второй критерий согласования источника с нагрузкой заключается в обеспечении максимума коэффициента полезного действия (КПД) цепи, который равен отношению активной мощности 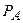 , потребляемой нагрузкой, к суммарной активной мощности в цепи
, потребляемой нагрузкой, к суммарной активной мощности в цепи
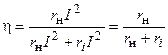 .
.
Зависимость КПД от резистивной составляющей сопротивления нагрузки показана на рис. 5.3, б. Из рисунка видно, что КПД цепи монотонно возрастает с ростом отношения 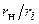 , приближаясь к единице
, приближаясь к единице 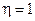 при
при 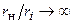 . Таким образом, для согласования источника с нагрузкой по критерию максимума КПД, необходимо, чтобы резистивная составляющая сопротивления нагрузки была намного больше резистивной составляющей внутреннего сопротивления источника (
. Таким образом, для согласования источника с нагрузкой по критерию максимума КПД, необходимо, чтобы резистивная составляющая сопротивления нагрузки была намного больше резистивной составляющей внутреннего сопротивления источника ( 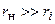 ).
).
Однако рассмотренные два критерия согласования источника энергии с нагрузкой не могут быть выполнены одновременно. Критерий максимума КПД применяется в основном в электротехнике в мощных электроэнергетических системах, а согласование по критерию максимума мощности, передаваемой в нагрузку, используется в радиотехнике в маломощных радиоэлектронных устройствах.
Тема 6. Анализ простейших электрических цепей при
гармоническом воздействии
Проанализируем методом комплексных амплитуд простейшие электрические цепи, составленные путем последовательного и параллельного соединения двух идеализированных пассивных элементов при гармоническом воздействии в виде напряжения
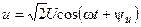 . (6.1)
. (6.1)
 где
где 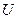 ,
, 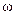 и
и 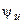 — действующее значение, круговая частота и начальная фаза напряжения.
— действующее значение, круговая частота и начальная фаза напряжения.
6.1. Последовательная RL-цепь при гармоническом воздействии
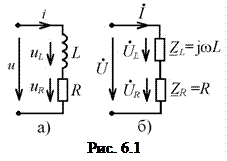
Рассмотрим последовательную RL-цепь (рис. 6.1, а). Заменяя в схеме (рис. 6.1) сопротивление 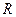 и индуктивность
и индуктивность 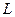 их комплексными схемами замещения
их комплексными схемами замещения 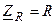 и
и 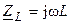 и переходя от вещественных функций тока
и переходя от вещественных функций тока 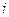 и напряжения
и напряжения 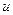 к комплексным действующим значениям
к комплексным действующим значениям 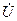 и
и 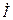 , получаем комплексную схему замещения (рис. 6.1, б).
, получаем комплексную схему замещения (рис. 6.1, б).
Тогда на основании закона Ома для участка цепи (4.21) составляем в комплексной форме уравнение электрического равновесия цепи (рис. 6.1, б)
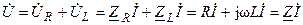 ,
,
где 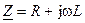 — комплексное сопротивление цепи в алгебраической форме записи.
— комплексное сопротивление цепи в алгебраической форме записи.
Преобразуем алгебраическую форму записи комплексного сопротивления RL-цепи в показательную
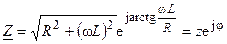 ,
,
где 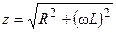 и
и 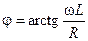 — модуль и аргумент комплексного сопротивления цепи.
— модуль и аргумент комплексного сопротивления цепи.
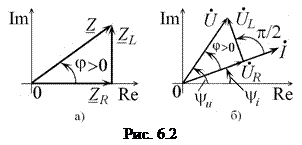 Комплексное сопротивление цепи может быть изображено на комплексной плоскости в виде вектора
Комплексное сопротивление цепи может быть изображено на комплексной плоскости в виде вектора 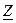 , равного геометрической сумме векторов
, равного геометрической сумме векторов  и
и 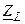 (рис. 6.2, а).
(рис. 6.2, а).
При конечных значениях 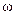 ,
, 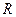 и
и 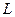 аргумент комплексного сопротивления последовательной RL-цепи имеет положительное значение и находится на интервале
аргумент комплексного сопротивления последовательной RL-цепи имеет положительное значение и находится на интервале 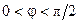 , что соответствует резистивно-индуктивному характеру сопротивления цепи. При рассмотрении Закона Ома в комплексной форме было показано, что аргумент комплексного сопротивления участка цепи равен фазовому сдвигу фаз между напряжением и током цепи. Откуда следует, что напряжение последовательной RL-цепи опережает по фазе её ток на угол
, что соответствует резистивно-индуктивному характеру сопротивления цепи. При рассмотрении Закона Ома в комплексной форме было показано, что аргумент комплексного сопротивления участка цепи равен фазовому сдвигу фаз между напряжением и током цепи. Откуда следует, что напряжение последовательной RL-цепи опережает по фазе её ток на угол 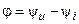 .
.
Используя закон Ома в комплексной форме, найдем комплексное действующее значение тока цепи
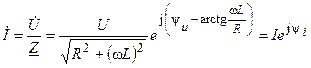 .
.
где 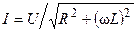 и
и 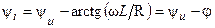 — модуль и аргумент комплексного действующего значения тока.
— модуль и аргумент комплексного действующего значения тока.
Переходя от изображения тока к его оригиналу, получаем
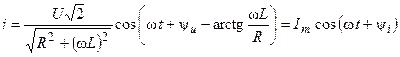 ,
,
где 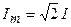 — амплитуда тока.
— амплитуда тока.
Таким образом, при известной частоте 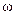 временная функция тока полностью определяются модулем и аргументом комплексного действующего значения этого тока. Поэтому при расчёте цепи достаточно найти только комплексные амплитуды или комплексные действующие значения токов и напряжений.
временная функция тока полностью определяются модулем и аргументом комплексного действующего значения этого тока. Поэтому при расчёте цепи достаточно найти только комплексные амплитуды или комплексные действующие значения токов и напряжений.
Векторная диаграмма комплексных тока и напряжений RL-цепи показана на рис. 6.2, б. Поскольку напряжение на сопротивлении совпадает по фазе с током, то вектор 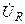 совпадает по направлению с вектором
совпадает по направлению с вектором 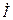 . Так как напряжение на индуктивности опережает по фазе ток на
. Так как напряжение на индуктивности опережает по фазе ток на 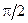 , то вектор
, то вектор 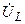 повернут относительно вектора
повернут относительно вектора 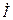 на угол
на угол 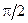 против часовой стрелки. В результате, вектор суммарного напряжения
против часовой стрелки. В результате, вектор суммарного напряжения 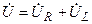 повернут относительно вектор тока
повернут относительно вектор тока 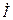 против часовой стрелки на угол
против часовой стрелки на угол 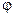 , равный аргументу комплексного сопротивления цепи. Откуда следует, что напряжение опережает по фазе ток на угол
, равный аргументу комплексного сопротивления цепи. Откуда следует, что напряжение опережает по фазе ток на угол 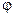 . Из рис. 6.2 видно, что «треугольник напряжений», образованный векторами
. Из рис. 6.2 видно, что «треугольник напряжений», образованный векторами 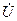 ,
, 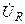 и
и 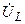 (рис. 6.2, б), подобен «треугольнику сопротивлений», образованному векторами
(рис. 6.2, б), подобен «треугольнику сопротивлений», образованному векторами 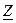 ,
,  и
и 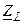 (рис. 6.2, а).
(рис. 6.2, а).
В прямоугольном «треугольнике напряжений» (рис. 6.2, б) действующие значения напряжений на входе цепи является гипотенузой, которая может быть выражена через катеты, представляющие собой действующие значения напряжений на элементах цепи
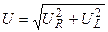 .
.
Лекция № 8
6.2. Последовательная RC-цепь при гармоническом воздействии
Схема последовательной RC-цепь при гармоническом воздействии (6.1) показана на рис. 6.3, а, а на рис. 6.3, б — её комплексная схема замещения.
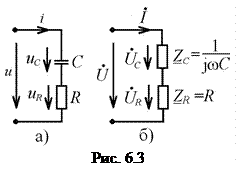 На основании закона Ома для участка цепи (4.21) составляем в комплексной форме уравнение электрического равновесия цепи (рис. 6.3, б)
На основании закона Ома для участка цепи (4.21) составляем в комплексной форме уравнение электрического равновесия цепи (рис. 6.3, б)
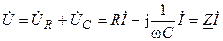 ,
,
где 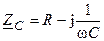 — комплексное сопротивление последовательной RC-цепи.
— комплексное сопротивление последовательной RC-цепи.
Запишем комплексное сопротивление последовательной RC-цепи в показательной форме
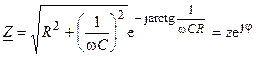 ,
,
где 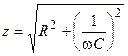 и
и 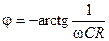 — модуль и аргумент комплексного сопротивления цепи соответственно.
— модуль и аргумент комплексного сопротивления цепи соответственно.
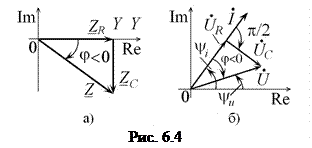
Векторная диаграмма комплексного сопротивления цепи показана на рис. 6.4, а.
Как и в случае последовательной RL-цепи (рис. 6.1, б) аргумент комплексного сопротивления RC-цепи равен фазовому сдвигу фаз между напряжением и током цепи. Однако при конечных значениях 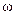 ,
, 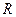 и
и 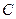 этот фазовый сдвиг отрицательный и находится на интервале
этот фазовый сдвиг отрицательный и находится на интервале 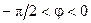 , что соответствует резистивно-емкостному характеру сопротивления цепи.
, что соответствует резистивно-емкостному характеру сопротивления цепи.
 Определим ток цепи, используя закон Ома в комплексной форме
Определим ток цепи, используя закон Ома в комплексной форме
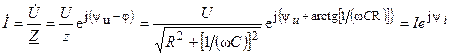 ,
,
где 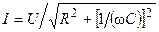 и
и 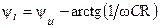 — модуль и аргумент комплексного действующего значения тока
— модуль и аргумент комплексного действующего значения тока
Векторная диаграмма комплексных напряжений и тока последовательной RC-цепь изображена на рис. 6.4, б, из которой видно, что напряжение цепи 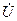 отстаёт по фазе от тока
отстаёт по фазе от тока 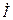 на угол j. В этом отношении последовательная RC-цепь дуальна последовательной RL-цепи.
на угол j. В этом отношении последовательная RC-цепь дуальна последовательной RL-цепи.
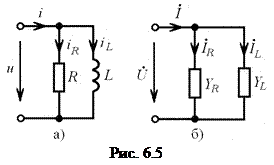
6.3. Параллельная RL-цепь при гармоническом воздействии
Рассмотрим параллельную RL-цепь (рис. 6.5, а) при гармоническом воздействии (6.1), а на рис. 6.5, б её комплексная схема замещения, где 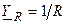 и
и 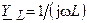 — комплексные проводимости сопротивления и индуктивности соответственно
— комплексные проводимости сопротивления и индуктивности соответственно
Составим для комплексной схемы замещения уравнение электрического равновесия на основании первого закона Кирхгофа в комплексной форме
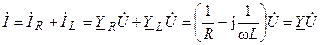 ;
;
где 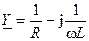 — комплексная проводимость параллельной RL-цепь.
— комплексная проводимость параллельной RL-цепь.
 Запишем комплексную проводимость параллельной RL-цепи в показательной форме
Запишем комплексную проводимость параллельной RL-цепи в показательной форме
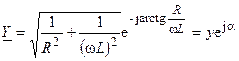 ,
,
где 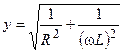 и
и 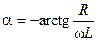 — модуль и аргумент комплексной проводимости параллельной RL-цепи соответственно.
— модуль и аргумент комплексной проводимости параллельной RL-цепи соответственно.
Поскольку комплексная проводимость есть величина обратная комплексному сопротивлению 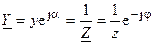 , то
, то 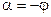 . Следовательно, аргумент комплексной проводимости участка цепи равен по абсолютной величине фазовому сдвигу фаз между напряжением и током цепи, но имеет противоположный знак, то есть
. Следовательно, аргумент комплексной проводимости участка цепи равен по абсолютной величине фазовому сдвигу фаз между напряжением и током цепи, но имеет противоположный знак, то есть 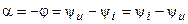 .
.
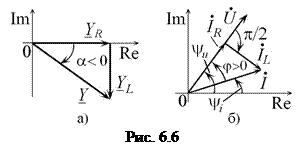 Векторная диаграмма комплексной проводимости параллельной RL-цепи показана на рис. 6.6, а. При конечных значениях
Векторная диаграмма комплексной проводимости параллельной RL-цепи показана на рис. 6.6, а. При конечных значениях 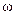 ,
, 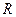 и
и 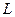 аргумент
аргумент 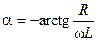 комплексной проводимости параллельной RL-цепи имеет отрицательное значение и находится на интервале
комплексной проводимости параллельной RL-цепи имеет отрицательное значение и находится на интервале 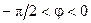 , что соответствует резистивно-индуктивному характеру проводимости цепи. Следовательно, напряжение параллельной RL-цепи опережает по фазе её ток на угол
, что соответствует резистивно-индуктивному характеру проводимости цепи. Следовательно, напряжение параллельной RL-цепи опережает по фазе её ток на угол 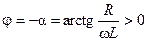 .
.
Используя закон Ома, найдем комплексное действующее значения тока цепи
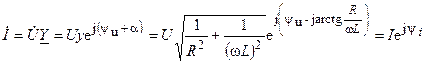 ,
,
где 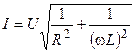 и
и 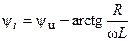 — модуль и аргумент комплексного действующего значения тока
— модуль и аргумент комплексного действующего значения тока
Векторная диаграмма комплексных токов и напряжения 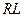 -цепи изображена на рис. 6.6, б, из которой видно, что напряжение
-цепи изображена на рис. 6.6, б, из которой видно, что напряжение 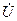 цепи опережает по фазе ток
цепи опережает по фазе ток 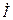 на угол
на угол  .
.
6.4. Параллельная RС-цепь при гармоническом воздействии
Рассмотрим параллельную 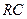 -цепь (рис. 6.7, а) при гармоническом воздействии (5.1).
-цепь (рис. 6.7, а) при гармоническом воздействии (5.1).
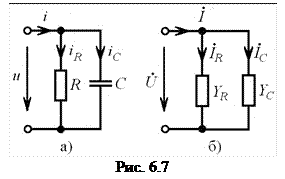 На рис. 6.7, б изображена схема замещения параллельной RC-цепи, где
На рис. 6.7, б изображена схема замещения параллельной RC-цепи, где 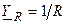 ;
; 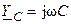 — комплексные проводимости сопротивления и ёмкости соответственно.
— комплексные проводимости сопротивления и ёмкости соответственно.
На основании первого закона Кирхгофа составим уравнение электрического равновесия цепи в комплексной форме
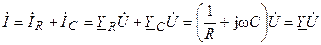 ;
;
где 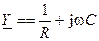 — комплексная проводимость параллельной RC-цепи.
— комплексная проводимость параллельной RC-цепи.
Запишем комплексную проводимость параллельной RC-цепи в показательной форме
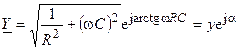 ,
,
где 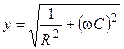 и
и 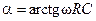 — модуль и аргумент комплексной проводимости параллельной RC-цепи.
— модуль и аргумент комплексной проводимости параллельной RC-цепи.
Векторная диаграмма комплексной проводимости параллельной RC-цепи показана на рис. 6.8, а. Поскольку аргумент комплексной проводимости находится на интервале 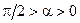 , то проводимость имеет резистивно-ёмкостной характер.
, то проводимость имеет резистивно-ёмкостной характер.
Используя закон Ома, найдем комплексное действующее значения тока цепи
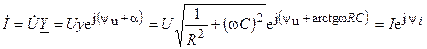 ,
,
где 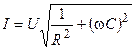 и
и 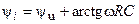 — модуль и аргумент комплексного действующего значения тока.
— модуль и аргумент комплексного действующего значения тока.
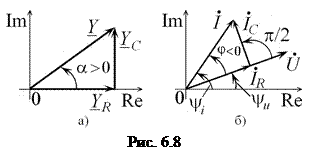 Векторная диаграмма комплексных напряжения и токов последовательной RC-цепи изображена на рис. 6.8 б, из которой видно, что напряжение
Векторная диаграмма комплексных напряжения и токов последовательной RC-цепи изображена на рис. 6.8 б, из которой видно, что напряжение 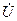 цепи отстаёт по фазе ток
цепи отстаёт по фазе ток 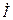 на угол
на угол  .
.
Анализ простейшие электрических цепей при гармоническом воздействии, выполненный с помощью метода комплексных амплитуд, показал следующее.
1) Комплексные сопротивление и проводимость участка цепи, содержащего хотя бы один реактивный элемент, зависят не только от параметров элементов цепи и вида их соединения между собой, но и от частоты гармонического воздействия.
2) При известной частоте гармонического воздействия для определения временные функции напряжений и токов цепи достаточно найти комплексные амплитуды или комплексные действующие значения этих напряжений и токов.
3) Фазовый сдвиг между входным напряжением и входным током цепи равен аргументу комплексного сопротивления цепи.
Тема 7. Преобразования электрических цепей
Расчёт сложной электрической цепи может быть упрощен путём замены отдельных участков этой цепи участков эквивалентными схемами замещения, имеющими более простую топологию по сравнению с заменяемыми участками.
7.1. Преобразование последовательной цепи в параллельную и обратно
Условием эквивалентных пассивных линейных двухполюсников является равенство их комплексных сопротивлений и проводимостей.
Пусть заданы параметры 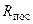 ,
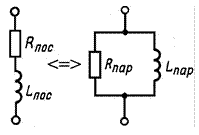
, 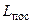 последовательной RL-цепи (рис. 7.3, а) и требуется найти параметры
последовательной RL-цепи (рис. 7.3, а) и требуется найти параметры 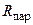 и
и 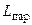 эквивалентной ей параллельной RL-цепи (рис. 7.3, б).
эквивалентной ей параллельной RL-цепи (рис. 7.3, б).
а) б) а) б)
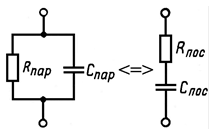
Рис. 7.3 Рис. 7.4
Определим комплексную проводимость последовательной RL-цепи
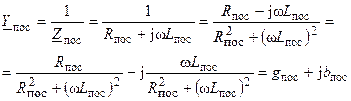
и комплексную проводимость параллельной цепи
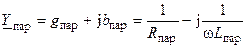 .
.
Приравнивая вещественные и мнимые составляющие комплексных проводимостей последовательной и параллельной цепей, находим
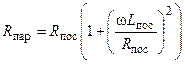 ;
; 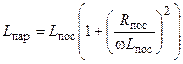 .
.
Если заданы параметры 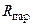 и
и 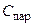 параллельной RС-цепи (рис. 7.4, а),. то она может быть аналогичным образом преобразована в эквивалентную ей последовательную RС-цепь (рис. 7.4, б), параметры которой определяются по формулам:
параллельной RС-цепи (рис. 7.4, а),. то она может быть аналогичным образом преобразована в эквивалентную ей последовательную RС-цепь (рис. 7.4, б), параметры которой определяются по формулам:
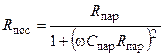 ;
; 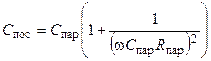 .
.
Таким же путём можно найти формулы для пересчёта параметров параллельной RL-цепи в последовательную, последовательной RC-цепи в параллельную и т.п.
Однако следует иметь в виду, что вышеприведенные эквивалентные преобразования применимы только для фиксированной частоты внешнего воздействия. Изменение частоты внешнего воздействия вызовет изменение значений параметров элементов эквивалентной цепи, поскольку частота входит в расчётные формулы.
