Закон Ома в комплексной форме для участка цепи
Составим компонентное уравнение участка электрической цепи (рис. 4.20) к которой приложено гармоническое напряжение. 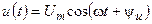 , где
, где 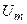 и
и 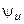 — амплитуда и начальная фаза напряжения
— амплитуда и начальная фаза напряжения
Поскольку цепь представляет собой последовательного соединения идеализированных сопротивления 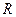 , индуктивности
, индуктивности 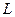 и ёмкости
и ёмкости 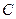 , то напряжение приложенное к цепи равно сумме напряжений на элементах цепи, которая с учётом (2.1), (2.5) и (2.10) представляет собой интегро-дифференциального уравнение
, то напряжение приложенное к цепи равно сумме напряжений на элементах цепи, которая с учётом (2.1), (2.5) и (2.10) представляет собой интегро-дифференциального уравнение
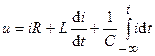 . (4.20)
. (4.20)
При гармоническом воздействии ток цепи в установившемся режиме будет также гармонической функцией времени той же частоты 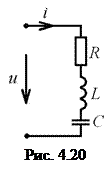 , что и частота напряжения, приложенного к цепи,
, что и частота напряжения, приложенного к цепи,
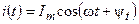 ,
,
где 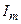 и
и 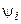 — амплитуда и начальная фаза тока.
— амплитуда и начальная фаза тока.
В соответствии с методом комплексных амплитуд, заменим в уравнении (4.20) оригиналы напряжения 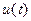 и тока
и тока 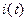 их изображениями в показательной форме записи
их изображениями в показательной форме записи 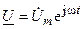 и
и 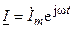
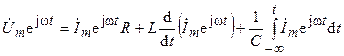 ,
,
где 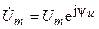 ,
, 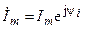 — комплексные амплитуды напряжения и тока.
— комплексные амплитуды напряжения и тока.
Полагая начальной напряжение на ёмкости равным нулю 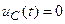 и преобразуя полученное уравнение, находим
и преобразуя полученное уравнение, находим
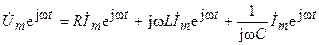 .
.
Сократив общий для всех членов уравнения множитель 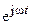 , получим
, получим
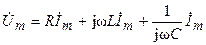 .
.
Тогда
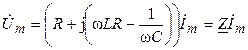 , (4.21)
, (4.21)
где 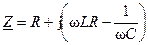 — комплексная функция, которая называется комплексным сопротивлением участка цепи.
— комплексная функция, которая называется комплексным сопротивлением участка цепи.
Видно, что комплексное сопротивление участка цепи, образованного путём последовательного соединении элементов, равно сумме комплексных сопротивлений этих элементов.
Запишем комплексное сопротивление участка цепи в показательной форме
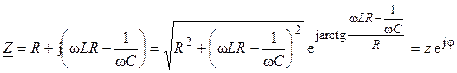 ,
,
где 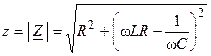 и
и 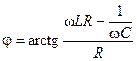 — модуль и аргумент комплексного сопротивления.
— модуль и аргумент комплексного сопротивления.
Решая уравнение (4.21) относительно комплексного сопротивления, находим
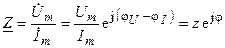 . (4.22)
. (4.22)
Откуда следует, что модуль комплексного сопротивления определяется отношением комплексных амплитуд или действующих значений напряжения и тока цепи
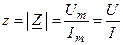
а аргумент — фазовым сдвигом между комплексными или вещественными функциями напряжения и тока цепи
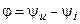 .
.
Если аргумент комплексного сопротивления равен нулю 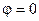 , то говорят, что сопротивление имеет резистивный (активный) характер. Если аргумент комплексного сопротивления равен
, то говорят, что сопротивление имеет резистивный (активный) характер. Если аргумент комплексного сопротивления равен 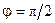 , то говорят, что сопротивление имеет индуктивный характер. Если аргумента сопротивления находится на интервале
, то говорят, что сопротивление имеет индуктивный характер. Если аргумента сопротивления находится на интервале 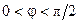 , то говорят, что сопротивление носит резистивно-индуктивный характер.
, то говорят, что сопротивление носит резистивно-индуктивный характер.
Величина, обратная комплексному сопротивлению (4.22), называется комплексной проводимостью участка цепи
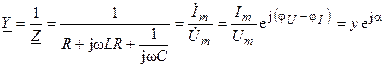 . (4.23)
. (4.23)
где 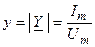 и
и 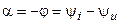 — модуль и аргумент комплексной проводимости цепи.
— модуль и аргумент комплексной проводимости цепи.
Из (4.23) следует, что аргумент комплексной проводимости цепи равен фазовому сдвигу между током и напряжением цепи. Если аргумент комплексной проводимости равен нулю 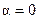 , то говорят, что проводимость имеет активный характер. Если аргумент комплексной проводимости равен
, то говорят, что проводимость имеет активный характер. Если аргумент комплексной проводимости равен 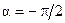 , то говорят, что проводимость имеет индуктивный характер. Если аргумент комплексной проводимости находится в интервале
, то говорят, что проводимость имеет индуктивный характер. Если аргумент комплексной проводимости находится в интервале 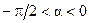 , то говорят, что проводимость имеет резистивно-индуктивный характер.
, то говорят, что проводимость имеет резистивно-индуктивный характер.
Уравнение (4.21) — (4.23) представляют собой разные формы записи законом Ома в комплексной формедля участка цепи. Аналогичным образом закон Ома в комплексной форме для участка цепи может быть записан для комплексных действующих значений тока 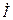 и напряжения
и напряжения 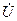 :
:
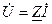 ;
; 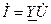 .
.
