Тема 2. Идеализированные элементы электрической цепи

Сопротивление

Сопротивлением называется идеализированный элемент цепи, способный необратимо преобразовывать электрическую энергию в другой вид энергии (тепловую, механическую и пр.). С этой точки зрения сопротивление является пассивным (диссипативным, то есть рассеивающим энергию) элементом электрической цепи.

Условное графическое изображение сопротивления показано на рис 2.1.

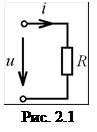Термин «сопротивление» и соответствующее ему условное обозначение 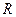используется в расчётных формулах для обозначения сопротивления как физической величины, а также в электрических схемах для обозначения резистора как элемента цепи. Наиболее близким к идеализированному сопротивлению по своим характеристикам является резистор.

Основной характеристикой сопротивления является вольтамперная характеристика, которая представляет собой зависимость напряжения на выводах сопротивления от проходящего через него тока (рис 2.2).

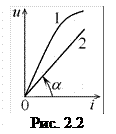Если вольтамперная характеристика сопротивления является нелинейной (рис 2.2, 1), то такое сопротивление называют нелинейным. При этом каждая точке вольтамперной характеристики ставится в соответствие статическое сопротивление 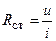и динамическое сопротивление 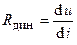, которые в общем случае не равны между собой .

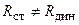Если вольтамперная характеристика сопротивления линейна (рис. 2.2, 2), то в этом случае сопротивление называют линейным, а его статическое и динамическое сопротивления одинаковы 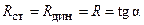и не зависят от напряжения и тока сопротивления.

Уравнение, связывающее ток и напряжение линейного сопротивления, определяется законом Ома, который был установлен Омом экспериментальным путём в 1826 г,

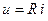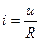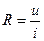; , . (2.1)

Величина обратная сопротивлению называется проводимостью и обозначается буквой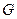

.

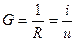В Международной системе единиц СИ сопротивление измеряется в омах (Ом), а проводимость — в сименсах (См). Поэтому сопротивление резисторов часто называют омическим

Мгновенная мощность, поступающая в сопротивление, всегда является положительной вещественной величиной

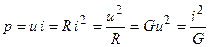. (2.2)

Электрическая энергия, поступающая в сопротивление и преобразующаяся в нём в другие виды энергии (тепловую, механическую и т.п.), также является положительной вещественной величиной

.

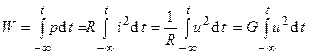Мкость

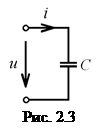
Емкостью называется идеализированный элемент электрической цепи, способный запасать энергию электрического поля. Условное графическое изображение емкости показано на рис. 2.3.

Наиболее близким к идеализированной емкости является конденсатор. Термин «ёмкость» и соответствующее ему условное обозначение используется в расчётных формулах для обозначения ёмкости как физической величины, а также в электрических схемах для обозначения конденсатора как элемента цепи.

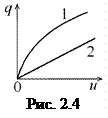Основной электрической характеристикой ёмкости является кулон-вольтная характеристика, которая представляет собой зависимость заряда 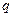, накопленного в ёмкости, от напряжения 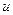на её выводах (рис 2.4) Если эта характеристика является нелинейной (рис 2.4, 1), то такая ёмкость называется нелинейной.

При этом каждой точке характеристики ставится в соответствие статическая ёмкость 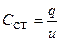и динамическая ёмкость 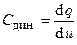, которые в общем случае не равны друг другу .

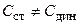Если кулон-вольтная характеристика ёмкости является линейно (рис. 2.4, 2), то такая ёмкость называется линейной, её статическая и динамическая емкости равны и не зависят от напряжения на ёмкости и запасённого в ней заряда

.

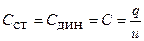В Международной системе единиц СИ емкость измеряется в фарадах (Ф = Кл/В).

Тогда заряд линейной ёмкости

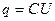. (2.3).

Подставляя (2.3) в (1.1), находим ток линейной емкости

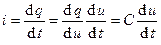. (2.4).

Если напряжение на емкости не изменяется во времени 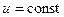, то в ёмкости существует постоянное электрическое поле. При этом из (2.4) следует, что ток емкости равен нулю, и, следовательно, её сопротивление на постоянном токе бесконечно велико. Если напряжение на емкости изменяется во времени, то в ёмкости существует переменное электромагнитной поле, которое движется внутри емкости от одной его обкладки к другой. При этом в цепи, подключенной к ёмкость, идёт переменный электрический ток, который называют током ёмкости.

Преобразуя (2.4), найдём напряжение ёмкости:

.

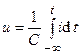В последнем выражении нижний предел интегрирования равен 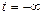, что позволяет учесть все изменения заряда в ёмкости, как бы давно они ни происходили. Если наблюдение за напряжением ёмкости начинается с некоторого момента времени 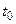, то последний интеграл можно представить в виде суммы

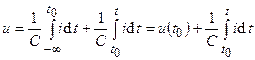, (2.5)

где 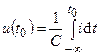— начальное напряжение на ёмкости в момент времени .

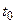Определим мгновенную мощность электрического поля ёмкости

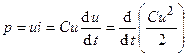. (2.6)

Приравнивая правые части уравнений (1.3) и (2.6), находим

.

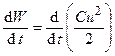Откуда получаем, что энергия электрического поля, запасенная ёмкостью, в произвольный момент времени определяется выражением

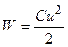(2.7)

и всегда имеет положительное значение.

Когда заряд ёмкости увеличивается, электрическая энергия из внешней цепи поступает в ёмкость, где она запасается в виде энергии электрического поля. О таком процессе говорят, что ёмкость заряжается. Когда заряд ёмкости уменьшается, ёмкость отдает накопленную энергию во внешнюю цепь. О таком процессе говорят, что ёмкость разряжается. Поскольку при этом никакого преобразования электрической энергии в другие виды энергии не происходит, то с энергетической точки зрения идеализированная ёмкость является пассивным энергоёмким или реактивным элементом электрической цепи.

Индуктивность

Индуктивностью называется идеализированный элемент электрической цепи, способный запасать энергию магнитного поля. Условное графическое изображение индуктивности показано на рис. 2.5.

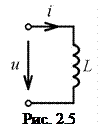Наиболее близким к идеализированной индуктивности является катушка индуктивности без ферромагнитного сердечника. Термин «индуктивность» и соответствующее ему условное обозначение 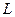используется в расчётных формулах для обозначения индуктивности как физической величины, а также в электрических схемах для обозначения катушки индуктивности как элемента цепи.

В соответствии с законом электромагнитной индукции Фарадея э.д.с., наводимая в индуктивности,

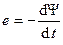, (2.8)

где 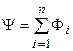— потокосцепление индуктивности; 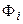— магнитный поток, пронизывающий 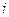-й виток индуктивности; 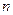— число витков индуктивности.

В общем случае магнитный поток, пронизывающий 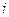-й виток индуктивности, можно представить в виде

,

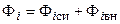где 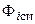— магнитный поток самоиндукции, который вызван электрическим током, протекающим в индуктивности; 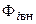— внешний магнитный поток, обусловленный внешними источниками магнитного поля.

Поэтому в общем случае потокосцепление индуктивности состоит из двух составляющих

,

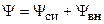где 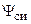— потокосцепление самоиндукции; 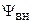— внешнее потокосцепление.

В результате, э.д.с., наведенная в индуктивности, может быть представлена в виде

.

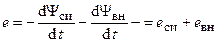где 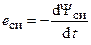— э.д.с. самоиндукции, вызванная изменением потокосцепление самоиндукции; 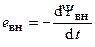— э.д.с., вызванная изменением внешнего потокосцепления.

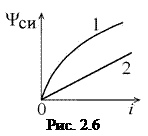Зависимость потокосцепления самоиндукции от тока индуктивности называется вебер-амперной характеристикой. Если эта характеристика является нелинейной (рис 2.6, 1), то такая индуктивность называется нелинейной. Каждой точке вебер-амперной характеристики ставится в соответствие статическая индуктивность 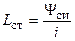и динамическая индуктивность 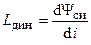, которые в общем случае не равны между собой . Если вебер-амперную характеристика линейная (рис 2.6, 2), то индуктивность называют линейной. В этом случае статическая и динамическая индуктивности равны и могут рассматриваться как коэффициент пропорциональности между потокосцеплением и током

.

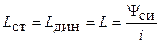Тогда потокосцепление прямо пропорционально току индуктивности

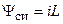. (2.9).

Если индуктивность линейная и отсутствует внешнее потокосцепление, то э.д.с. самоиндукции, наводимая в индуктивности, определяется с учётом (2.8) и (2.9) по формуле

.

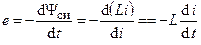При анализе цепей положительное направление напряжения на выводах индуктивности выбирают совпадающим с положительным направлением тока, то есть противоположным направлению э.д.с. самоиндукции (рис. 2.5),

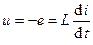. (2.10)

Из (2.10) следует, что при протекании через индуктивность постоянного тока напряжение на индуктивности равно нулю и, следовательно, её сопротивление на постоянном токе также равно нулю. Решая уравнение (2.10) относительно тока 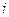, находим

.

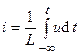В последнем выражении нижний предел интегрирования равен 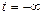, что позволяет учесть все изменения потокосцепления индуктивности, как бы давно они ни происходили. Если ток индуктивности определяется, начиная с некоторого момента времени 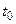, то последний интеграл можно представить в виде

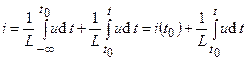, (2.11)

где 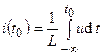— ток индуктивности в момент .

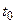С учётом (2.10) определим мгновенную мощность индуктивности

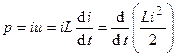. (2.12)

Приравнивая правые части уравнений (1.3) и (2.12), находим

.

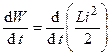Откуда следует, что энергия магнитного поля, запасенная индуктивностью, в произвольный момент времени определяется выражением

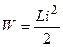,. (2.13)

и всегда имеет положительное значение.

Таким образом, с энергетической точки зрения индуктивность является пассивным элементом электрической цепи, который при возникновении в нем электрического тока запасает энергию в виде энергии магнитного поля и отдает эту энергию в процессе исчезновения этого тока. Поэтому идеализированные индуктивность называют пассивным энергоемким или реактивным элементом электрической цепи по аналогии с идеальной ёмкостью.