Определение характеристик цифровых

Элементарных ячеек

2.4.1. Как известно, основной характеристикой линейной цифровой частотно-избирательной цепи, которая также называется цифровым фильтром (ЦФ), является ее передаточная функция , которая представима в виде

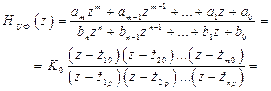
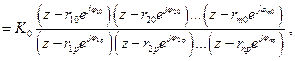(2.10)

где 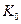– коэффициент пропорциональности; 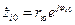– нули; 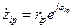– полюса; 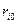и 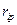– модули 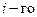нуля и 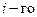полюса; 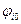и 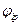– фазовые углы 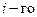нуля и 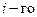полюса; 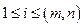; 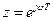– независимая переменная; 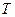– период дискретизации, определяемый из условия выполнения теоремы Котельникова; 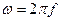(рад/с) – круговая частота; 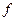(Гц) – частота. Для физически реализуемых систем порядки полиномов числителя и знаменателя должны быть .

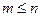Выражение (2.10) при 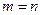можно представить в виде

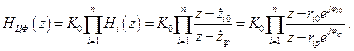(2.11)

Отношение полиномов первого порядка в (2.11) описывает передаточную функцию 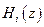цифровой комплексной ячейки первого порядка. Тогда, опуская индекс 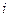, можно записать ее передаточную функцию в виде

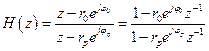. (2.12)

Числитель в выражении (2.12) описывает передаточную функцию цифровой элементарной нерекурсивной ячейки, а знаменатель – рекурсивной.

В том случае, когда в (2.11) полюса и нули являются попарно комплексно-сопряженными, передаточная функция описывает соответственно рекурсивную и нерекурсивную биквадратные ячейки, которые имеют второй порядок каждая.

Передаточная функция элементарной биквадратной ячейки имеет вид

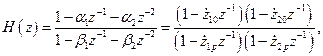(2.13)

где ; ; ; ; .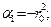

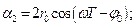
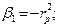
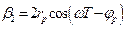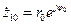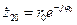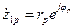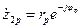Видно, что биквадратная ячейка, описываемая выражением (2.13), представляет собой каскадное соединение элементарных ячеек первого порядка с комплексно-сопряженными нулями и полюсами.

2.4.2. Нерекурсивная ячейка первого порядка.

2.4.2.1. Существуют нерекурсивные ячейки двух видов. Передаточная функция нерекурсивной ячейки первого вида, полученная непосредственно из (2.12), будет

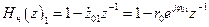. (2.14)

Импульсная характеристика (ИХ) этой ячейки определяется следующим образом.

Перепишем выражение (2.14) в виде

.

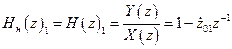Тогда

.

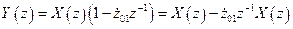Выполняя обратное Z-преобразование над последним выражением, получим дискретную форму записи в виде [1]

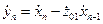. (2.15)

Поскольку работа любой цепи начинается в момент времени 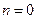, то величина .

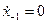Тогда выходной отклик 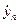из выражения (2.15) для последовательности входных данных 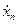в каждый 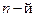момент времени будет

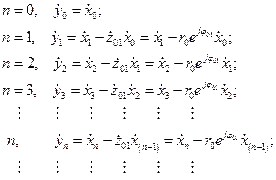(2.16)

Для определения ИХ любой цепи используется входная импульсная последовательность в виде цифровой « 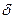-функции», которая представляет собой единичную функцию 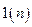в момент времени 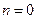, т.е. 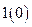, длительностью 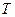(с).

Тогда, при 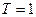, входные данные будут иметь вид

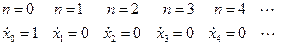(2.17)

Подавая входные отсчеты (2.17) в (2.16) получим ИХ нерекурсивной комплексной ячейки первого вида

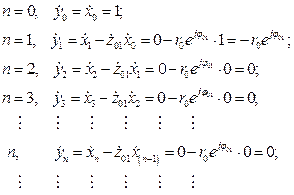
Таким образом, ИХ нерекурсивной ячейки первого вида в соответствующие моменты времени 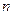будет

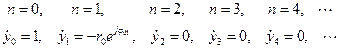
Определим амплитудно-частотную характеристику (АЧХ) нерекурсивной ячейки. Для этого подставим в (2.14) величины 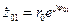и 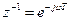. В результате получим

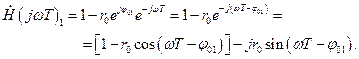
Для нахождения АЧХ необходимо найти модуль последнего выражения. По определению, модуль комплексного числа .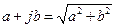

Тогда будем иметь

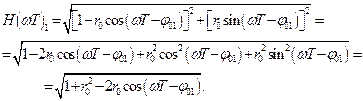(2.18)

Очевидно, что минимальное значения выражение (2.18) примет при 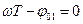(рад), т.е. тогда, когда 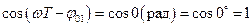и будет равно

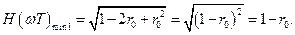(2.19)

Максимальное значение в (2.18) будет при 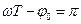(рад), т.е. 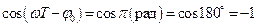и будет равно

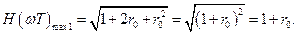(2.20)

Для получения АЧХ в нормированном виде нужно выражение (2.18) разделить на (2.20), откуда

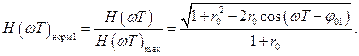(2.21)

На практике наиболее часто встречается случай, когда величина 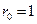. Тогда выражение (2.18) примет вид

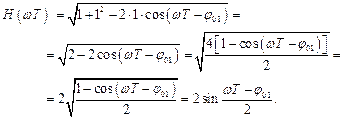(2.22)

Когда величина 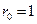, то выражение (2.19) будет равно нулю, выражение (2.20) будет равно 2, а выражение (2.21) будет иметь вид

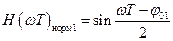. (2.23)

Из (2.23) видно, что АЧХ представляет собой половину синусоиды в диапазоне 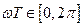(рад) нормированной частоты 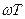, причем ее нуль находится в точке 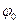на оси частот.

Положение нуля передаточной функции 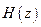на Z-плоскости будет:

для 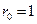– на единичной окружности;

для 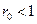– внутри единичной окружности;

фазовый угол будет равен величине .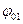

На рис. 6 изображены формы ненормированной АЧХ нерекурсивной ячейки первого вида при различных значениях параметров 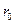и 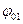, рассчитанные по формулам (2.18) и (2.22).

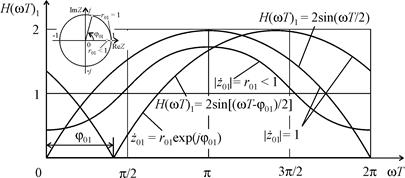Рис. 6. Формы ненормированной АЧХ нерекурсивной ячейки первого вида

На рис. 7 изображена структурная схема нерекурсивной ячейки первого вида.

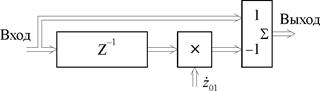Рис.7. Структурная схема нерекурсивной ячейки первого вида

2.4.2.2. Передаточная функция нерекурсивной ячейки второго вида, записывается в форме

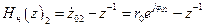. (2.24)

Для этой ячейки ИХ определяется следующим образом.

Перепишем выражение (2.24) в виде

.

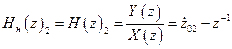Тогда

.

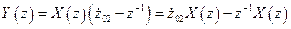Выполняя обратное Z-преобразование над последним выражением, получим дискретную форму записи в виде [1]

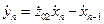. (2.25)

Тогда выходной отклик 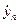из выражения (2.25) для последовательности входных данных 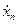в каждый 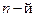момент времени будет

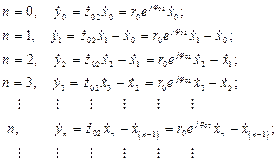(2.26)

Аналогично описанному выше, подавая входные данные (2.17) на (2.26) будем иметь ИХ нерекурсивной цифровой комплексной ячейки второго вида

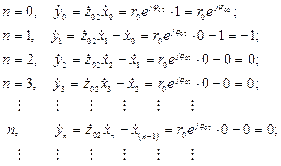
Таким образом, ИХ нерекурсивной ячейки второго вида в соответствующие моменты времени 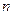будет

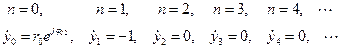
Определим АЧХ нерекурсивной ячейки второго вида. Для этого подставим в (2.24) величины 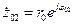и 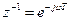. В результате получим

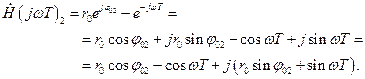
Далее, для нахождения АЧХ необходимо найти модуль последнего выражения.

Тогда будем иметь

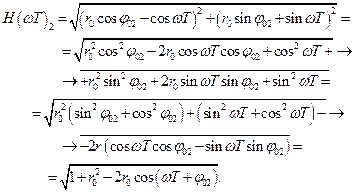(2.27)

Сравнивая (2.18) с (2.27) можно видеть, что АЧХ обоих видов нерекурсивных ячеек отличаются только знаком у параметра 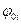, т.е. если 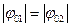, то 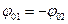. Следовательно их АЧХ будут одинаковыми, только положение нулей будут смещены в противоположных направлениях относительно точки нуль на оси частот.

На рис. 8 изображены формы ненормированной АЧХ нерекурсивной ячейки второго вида при различных значениях параметров 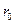и .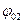

Рис. 8. Формы ненормированной АЧХ нерекурсивной ячейки второго вида

На рис. 9 изображена структурная схема нерекурсивной ячейки второго вида.

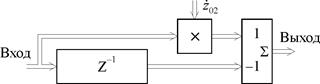Рис.9. Структурная схема нерекурсивной ячейки второго вида

2.4.3. Рекурсивная ячейка. Передаточная функция рекурсивной ячейки, полученная непосредственно из (2.12), будет

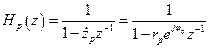. (2.28)

Для этой ячейки ИХ определяется аналогично тому, как определялась ИХ для нерекурсивной ячейки, т.е. полагаем, что

.

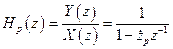Отметим, что для устойчивой работы рекурсивной ячейки необходимо, чтобы выполнялось условие 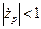или .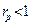

Далее, производя простейшие операции, получаем

,

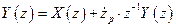откуда, производя обратное Z-преобразование, будем иметь отсчеты временной функции в виде

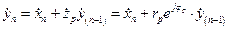. (2.29)

Поскольку работа любой цепи начинается в момент времени 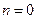, то величина .

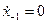Выходной отклик 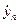из выражения (2.29) для последовательности входных данных 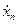в каждый 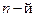момент времени будет

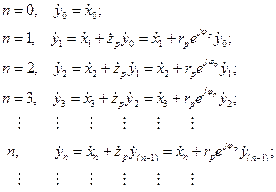(2.30)

Подавая входные данные (2.17) на (2.30), получим

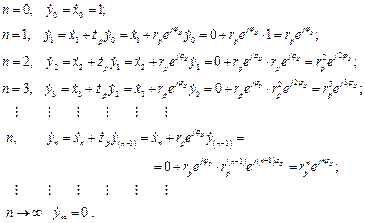(2.31)

Таким образом, ИХ рекурсивной ячейки в соответствующие моменты времени 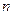будет

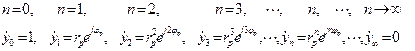
Видно, что отсчеты ИХ в (2.31) рекурсивной ячейки представляют собой геометрическую прогрессию со знаменателем прогрессии .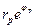

АЧХ рекурсивной ячейки определяется аналогично тому, как определялась для нерекурсивных ячеек.

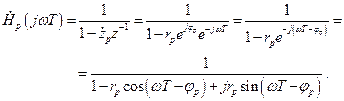. (2.32)

Далее, для нахождения АЧХ определим модуль выражения (2.32) в виде

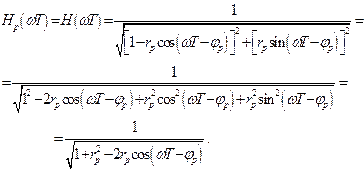(2.33)

Максимальное и минимальное значения АЧХ рекурсивной ячейки будут при значениях 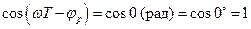и при значениях 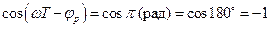в выражении (2.33)

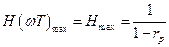и .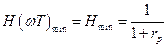

Нормированная АЧХ будет иметь вид

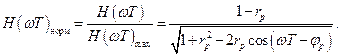(2.34)

На рис. 10 изображена нормированная АЧХ рекурсивной ячейки.

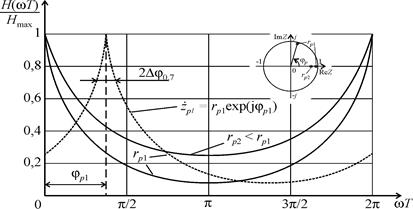Рис. 10. Нормированная АЧХ рекурсивной ячейки

На рис. 11. изображена структурная схема цифровой комплексной рекурсивной ячейки первого порядка.

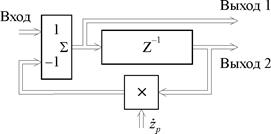Рис. 11. Структурная схема цифровой комплексной рекурсивной ячейки первого порядка

Пример 7. По передаточной функции цифрового фильтра на Z-плоскости 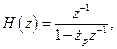где 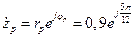, записать последовательность отсчетов для его ИХ, рассчитать и построить АЧХ, нарисовать на Z-плоскости положение полюса, нарисовать его структурную схему.

.

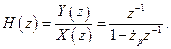
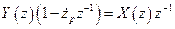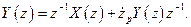
Производя обратное Z-преобразование над последним выражением, получаем

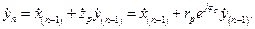
Подавая входные данные 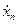в соответствующие моменты времени и учитывая, что 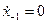, будем иметь

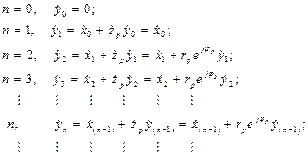(2.35)

Подавая входные данные (2.17) на (2.30), получим

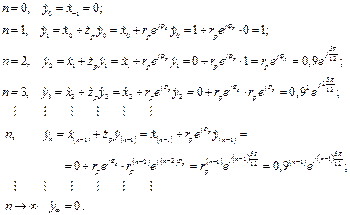(2.36)

Таким образом, из выражения (2.36) видно, что отсчеты ИХ рекурсивной ячейки в моменты времени 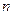будут

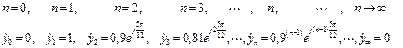
АЧХ рекурсивной ячейки будет

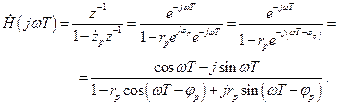. (2.37)

Определим модуль АЧХ рекурсивной ячейки, которая описывается выражением (2.37)

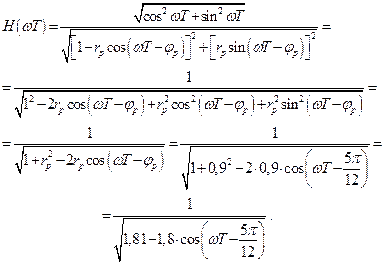
Максимум будет на частоте 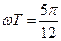(рад) и равен величине

.

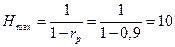Минимум будет на частоте (рад) и равен величине

.

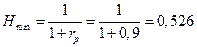Для нормированного случая

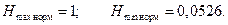
Вид нормированной АЧХ изображен на рис. 10 пунктиром. Там же изображено положение полюса для этого случая.

Структурная схема рекурсивной ячейки изображена на рис. 11, причем для рассматриваемого примера используется второй выход.

Аналогичным образом решаются все задачи в п.10.1.7. в [2].