А. Метод вероятностной бумаги
График функции распределения 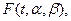 можно представить в виде совокупности точек (t, p) на плоскости, где
можно представить в виде совокупности точек (t, p) на плоскости, где 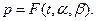
Основная идея графического метода состоит в том, что подбирается такая непрерывная замена координат 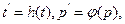 что при этом график функции распределения
что при этом график функции распределения 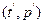 , где
, где 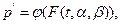 становится прямой линией
становится прямой линией 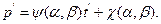 Если такую замену переменных удалось отыскать, то на плоскости
Если такую замену переменных удалось отыскать, то на плоскости 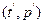 любая функция распределения этого семейства будет представима в виде прямой
любая функция распределения этого семейства будет представима в виде прямой 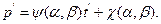 Или, что то же самое, в виде прямой
Или, что то же самое, в виде прямой
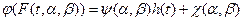 ……………………..(1).
……………………..(1).
Используем этот факт для оценки параметров 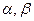 . Предположим, что в результате испытаний получены N значений (в нашем случае N=100) некоторой случайной величины (например, времени безотказной работы элемента или интервалов между отказами в аппаратуре).
. Предположим, что в результате испытаний получены N значений (в нашем случае N=100) некоторой случайной величины (например, времени безотказной работы элемента или интервалов между отказами в аппаратуре).
По этим значениям мы построили эмпирическую функцию распределения. Полученная эмпирическая функция при больших N лежит вблизи от теоретической функции распределения 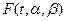 . Тогда после замены переменных график
. Тогда после замены переменных график 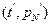 будет лежать в непосредственной близости от графика
будет лежать в непосредственной близости от графика 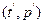 , являющегося прямой вида (1). Оценив тангенс наклона k и свободный член b, и приравняв их теоретическим значениям, получаем уравнения
, являющегося прямой вида (1). Оценив тангенс наклона k и свободный член b, и приравняв их теоретическим значениям, получаем уравнения
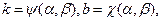 ……………………………………(2)
……………………………………(2)
из которых находим оценки неизвестных значений параметров 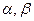 .
.
Найдем параметры a, b распределения Вейбулла:
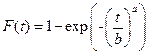
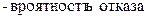
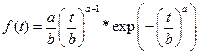
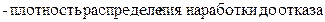
Произведем расчет параметров a и b:
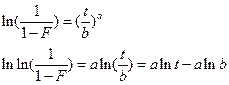
Произведем замену
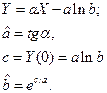
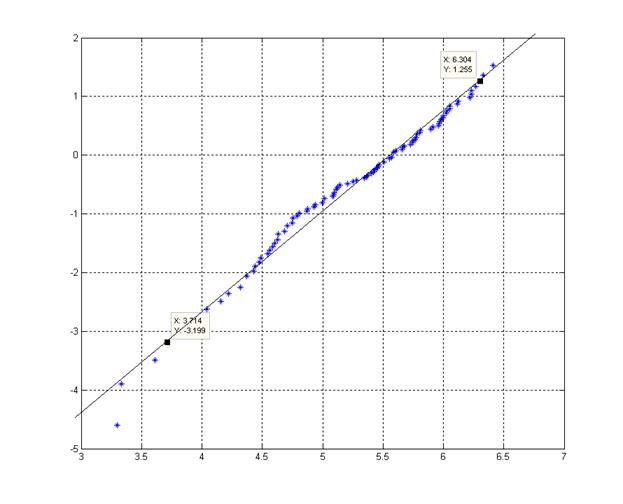
Рисунок 4: График Y(X) для метода вероятностной бумаги
Усреднив полученные значения, получили прямую, по двум точкам было построено уравнение прямой, оно имеет следующий вид:
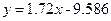
Откуда, с учетом вышеперечисленных формул, получаем:
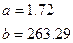
Построим график распределения Вейбулла с полученными коэффициентами:
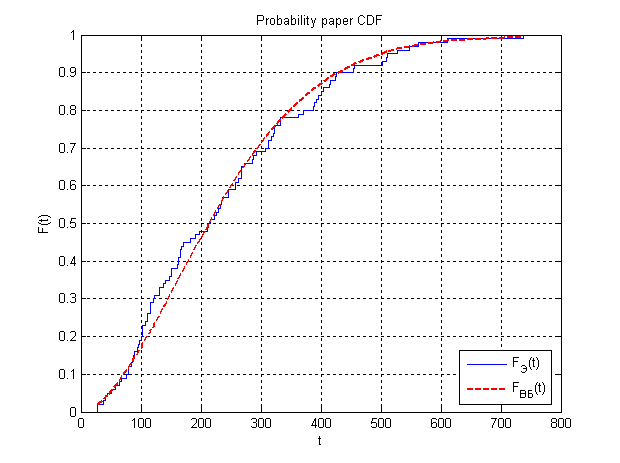
Рисунок 5: График эмпирической функции вместе с графиком распределения Вейбулла, коэффициенты которого найдены по методу вероятностной бумаги.
Произведем оценку максимальной удаленности графика распределения Вейбулла от эмпирической функции:
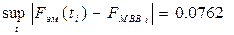
5.6 Сводка результатов, их анализ и выводы
Для облегчения анализа сведем полученные результаты в таблицы. Прежде всего, приведем результаты оценок выборочных начальных и центральных моментов.
Начальные моменты: 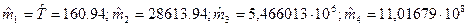 .
.
Таблица. Оценки центральных моментов
| Метод расчета | Дисперсия | с.к.о | Skewness | Excess |
| По найденным начальным | 2712.2564 | 52.07933 | -0.0859109 | -0.677924 |
| По выборке | 2712.2564 | 52.07933 | -0.0859109 | -0.677924 |
| Несмещенные оценки | 2767.6086 | 52.60806 | -0.0885911 | - 0.591176 |
Прежде всего, отметим отрицательную асимметрию эмпирического распределения, которая подтверждается во всех методах расчета. Отметим также факт сходства в оценках всех коэффициентов по выборочным начальным моментам и непосредственно по выборке.
Естественно принять для «разгадывания» распределений и оценки их параметров методами моментов и максимального правдоподобия несмещенные оценки центральных моментов, то есть:
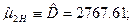
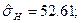
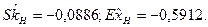 Таблица.
Таблица.
Результаты оценок для Гамма-распределения
с параметрами, полученными методом МОМЕНТОВ и
методом МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ.
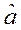 | 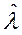 | с.к.о | Skewness | Excess | Параметры 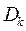 и и 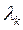 критерия Колмогорова критерия Колмогорова | |
| Метод моментов | 9.3589 | 0.0582 | 52.5641 | 0.65376 | 0.6411 | 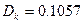 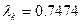 |
| Метод максимального правдоподобия | 8.1753 | 0,06078 | 47.0426 | 0.69948 | 0.7339 | 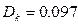 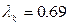 |
Из таблицы видно, что полученные оценки коэффициентов асимметрии и эксцесса полученных аппроксимирующих гамма-распределений положительны, что противоречит эмпирическим оценка. И гипотезу о гамма-распределении можно было бы и не рассматривать. Однако критерий согласия Колмогорова при уровне значимости 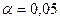 выполняется
выполняется 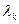 < критического значения
< критического значения 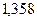 1. То есть, нет оснований для отрицания гипотезы о принадлежности выборки гамма-распределению. В этом вскрывается проблематичность практического использования критерия согласия Колмогорова. И если бы мы не оценивали третий и четвертый центральные моменты, то всегда бы совершили непоправимую ошибку!
1. То есть, нет оснований для отрицания гипотезы о принадлежности выборки гамма-распределению. В этом вскрывается проблематичность практического использования критерия согласия Колмогорова. И если бы мы не оценивали третий и четвертый центральные моменты, то всегда бы совершили непоправимую ошибку!
Обратимся к результатам для распределения Вейбулла, приведенным в таблице.
Таблица.
Результаты оценок для распределения Вейбулла
с параметрами, полученными методом МОМЕНТОВ и
методом МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ.
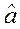 | 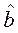 | с.к.о | Sk | Ex | Параметры 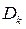 и и 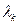 критерия Колмогорова критерия Колмогорова | |
| Метод моментов | 3.3765 | 179,209 | 52.6646 | 0.0017499 | 1551.866525 |  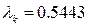 |
| Метод максимального правдоподобия | 3.4828 | 179,173 | 51.2941 | 0.00068932 | 1922.615176 | 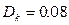 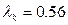 |
И сразу же заметим, что и для распределения Вейбулла критерий согласия Колмогорова также не отвергает этой гипотезы. Однако оценки коэффициентов асимметрии и эксцесса, полученные аппроксимирующими распределениями Вейбулла, не совпадают с эмпирическими, что говорит о том, что формулы
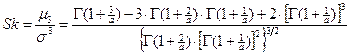
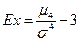 , где
, где 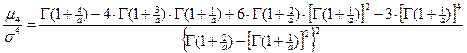
требуют тщательной проверки.
По результатам исследования может быть сделан вывод о том, что с вероятностью 0,95 эмпирическое распределение принадлежит теоретическому распределению Вейбулла с параметрами, полученными методом моментов, так как в целом «ближе» к выборочным.
Отметим также, что распределение Вейбулла при 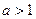 является стареющим, в отличии от Гамма-распределения, которое всегда имеет, во-первых положительную асимметрию, а во-вторых является нестареющим (так как интенсивность отказов или опасность таких объектов всегда ограничена значением параметра
является стареющим, в отличии от Гамма-распределения, которое всегда имеет, во-первых положительную асимметрию, а во-вторых является нестареющим (так как интенсивность отказов или опасность таких объектов всегда ограничена значением параметра 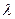 этого распределения).
этого распределения).
Используя критериальные неравенства для «стареющего» распределения, проведем оценку на базе первых начальных моментов по программе в среде ПК МВТУ.
Программа14
t=time;
{Расчет и оценка критерия "стареющего распределения }
M1=160.94; {т.е. M1=m1=T}
M2=161.1/2; {т.е. M2=m2/2!; m2=27945}
M3=161.26/6; {т.е. M3=m3/3!; m3=5031300;}
M4=160.3/24; {т.е. M4=m4/4!; m4=730570000}
Delt1=(M2^2-M1*M3);
Delt2=(M3^2-M2*M4);
Nerav1=sign(M2^2-M1*M3);
Nerav2=sign(M3^2-M2*M4);
output Nerav1,Nerav2,Delt1,Delt2;
Результат таков:
Оба неравенства выполнились. Правая часть каждого неравенства много больше левой части. Это говорит о том, что распределение стареющее. Таким образом, делаем окончательный вывод о принадлежности выборочного распределения распределению Вейбулла.
При выполнении настоящей работы отработаны вычислительные методы и в среде программного комплекса «МВТУ» разработано соответствующее алгоритмическое обеспечение. При этом обеспечивается решение сложных нелинейных алгебраических уравнений и полностью исключается применение таблиц.
Выводы
При выполнении работы развиты известные и предложены новые вычислительные процедуры и алгоритмы и разработано программное обеспечение информационных систем обработки статистической информации, получаемой из сферы эксплуатации, для решения задач объективной оценки характеристик и показателей надежности оборудования с использованием методов моментов, вероятностной бумаги и максимального правдоподобия для полных и цензурированных выборок без обращения к огромному числу таблиц. Эффективность предложенных алгоритмов проверена при решении конкретных задач. В работе сделан научно-технический задел для решения на ЭВМ перспективных задач обработки информации с малыми или ограниченными по объему выборками, в том числе с различными типами цензурирования, то есть усеченными выборками, методами моментов и максимального правдоподобия, как с точечными, так и интервальными оценками параметров предполагаемых распределений.
Список использованной литературы
1. Справочнике «Надежность технических систем» под ред И.А. Ушакова. – М.: «Радио и связь». 1985.
2. РД 50-690-89 «Методические указания. Надежность в технике. Методы оценки показателей надежности по экспериментальным данным». – М.: Изд-во стандартов, 1989.
3. Е.С. Вентцель. Теория вероятностей. – М.: Физматгиз, 1962
4. Г. Хан, С. Шапиро. Статистические модели в инженерных задачах: Пер. с англ. – М.: Изд-во «МИР», 1969.
5. Крамер. Математические методы статистики: Пер. с англ. – М.: Изд-во «МИР», 1975.
6. ГОСТ Р 50779.27-2007. Статистические методы. Критерии согласия и доверительные интервалы для распределения Вейбулла.
7. ГОСТ 11.008-75. Правила построения и применения вероятностных сеток.Приложение 1 (справочное)
Стандартные распределения и их свойства и характеристики
