Выбор вида модели с распределительным лагом

Количественно измерить силу связи между результатом и значениями факторной переменной, относящихся к различным моментам времени можно с помощью коэффициентов регрессии при факторных переменных.

Если с ростом величины лага коэффициенты при лаговых значениях переменной убывают во времени, то имеет место линейная (а) или геометрическая (б) структура лага. Если структура лага имеет вид, изображенный на рис.(в), то структура называется “перевернутой” или V-образной.

Структуры, изображенные на рис.(г), (д) и (е) свидетельствуют о полиномиальной структуре лага.

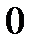
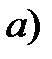
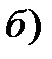
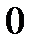
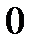
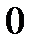
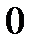
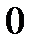
Рис.7.1. Графическое изображение структуры лага

Пусть задана модель с распределенным лагом, имеющим конечную максимальную величину лага :

Предположим, что в исследуемой модели имеет место полиномиальная структура лага, т.е. зависимость коэффициентов регрессии от величины лага описывается полиномом k-ой степени.

Лаги, структуру которых можно описать с помощью полиномов, называют лагами Алмон (по имени Ш. Алмон).

Модель зависимости коэффициентов от величины лага j в форме полинома можно записать в следующем виде:

- для полинома 1-й степени: ;

- для полинома 2-й степени: ;

- для полинома k-й степени: .

Тогда для коэффициентов модели можно получить формулы:

;

;

; (7.5)

………………………

.

Подставив в модель найденные соотношения для b_j и, выполнив преобразования, окончательно получим:

, (7.6)

где ; ,…. (7.7)

Процедура применения метода Алмон для расчета параметров модели с распределенным лагом включает следующие шаги:

­ определяется максимальная величина лага ;

­ определяется степень полинома k, описывающего структуру лага;

­ по формулам (7.7) рассчитываются значения переменных z ,z ,…, z ;

­ определяются параметры с уравнения линейной регрессии (7.6);

­ с помощью соотношений (7.5) рассчитываются параметры исходной модели с распределенным лагом.

Использование метода Алмон сопряжено с рядом проблем:

­ во-первых, величина лага должна быть известна заранее. Существует несколько способов определения реальной величины лага, например, построение нескольких уравнений регрессии и выбор наилучшего из них.

Наиболее простым способом является измерение тесноты связи между результатом и лаговыми значениями фактора;

­ во-вторых, необходимо установить степень полинома k. Обычно на практике ограничиваются рассмотрением полиномов 2-й и 3-й степени, применяя следующее правило: степень полинома k должна быть на единицу больше числа экстремумов в структуре лага.

К преимуществам метода Алмон относятся:

- универсальность т.к. может быть применен для моделирования процессов с разнообразными структурами лагов;

- возможность, при относительно небольшом количестве переменных (обычно k=2,3), построения модели с распределенным лагом любой длины.

Рассмотренный выше метод применим в предположении конечной длины лага .

Пусть теперь рассматривается модель с бесконечным лагом вида:

. (7.8)

Определить параметры такой модели обычным МНК или с помощью других статистических методов нельзя, т.к. число факторов модели - бесконечно.

Однако при определенных допущениях, а именно, когда структура лага является геометрической, т.е. когда воздействия лаговых значений фактора на результат уменьшаются с увеличением величины лага в геометрической прогрессии, оценки параметров модели можно получить. Один из таких подходов, впервые был предложен Л.М. Койком. Основное предположение Койка состоит в том, что существует некоторый постоянный темп (0< <1) уменьшения во времени лаговых воздействий фактора на результат, т.е.

. (7.9)

Тогда модель (7.8) запишется в виде

(7.10)

Для момента (t-1) модель (7.10) примет вид:

где .

Полученная модель является моделью авторегрессии, с параметрами, , и .

Далее по формулам (7.9) определяем .

Величины среднего и медианного лагов в модели Койка определяются по формулам:

(7.11)

(7.12).