Моделирование тенденций временного ряда. Адаптивные модели прогнозирования

Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени или тренда. Этот способ называют аналитическим выравниванием временного ряда.

Для построения трендов чаще всего применяются следующие функции:

­ линейный тренд: ;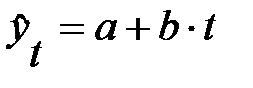

­ гипербола: ;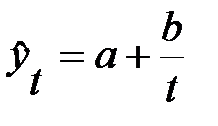

­ экспоненциальный тренд: 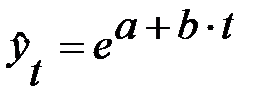или ;

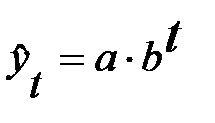­ полиномиальный тренд:

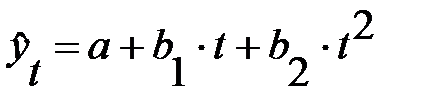- полином 2-й степени;

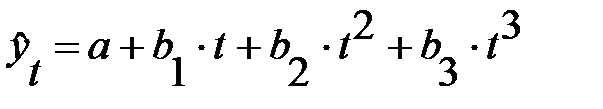- полином 3-й степени.

Параметры каждого из перечисленных трендов можно определить обычным МНК.

Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени. В этих целях можно использовать коэффициенты автокорреляции уровней ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни у 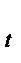и у_t-1 тесно коррелируют. В этом случае коэффициент автокорреляции 1-го порядка уровней исходного ряда должен быть высоким.

Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации `R 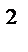и выбора уравнения тренда с максимальным значением `R . Реализация этого метода относительно проста при компьютерной обработке данных.

При наличии неявной нелинейной тенденции следует дополнять описанные выше методы качественным анализом динамики изучаемого показателя, с тем, чтобы избежать ошибок спецификации при выборе вида тренда.

Качественный анализ предполагает изучение проблем возможного наличия в исследуемом временном ряде поворотных точек и изменения темпов прироста, начиная с определенного момента. В случае если уравнение тренда выбрано неверно при больших значениях t, результаты прогноза на основе выбранного вида тренда будут недостоверными.

Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания.

Рассмотрим простейший подход – построение аддитивной или мультипликативной модели временного ряда методом скользящей средней.

Аддитивная и мультипликативная модели математически записываются соответственно

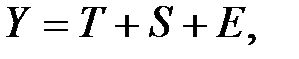(5.5)

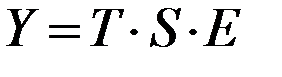(5.6)

где T, S, E – трендовая, сезонная и случайная компоненты, соответственно.

Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, если она возрастает или уменьшается, строят мультипликативную модель временного ряда.

Процесс построения модели включает следующие шаги:

­ выравнивание исходного ряда методом скользящей средней;

­ расчет значений сезонной компоненты S;

­ устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных ( 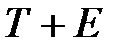) в аддитивной или ( 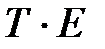) в мультипликативной модели;

­ аналитическое выравнивание уровней ( 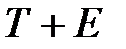) или ( 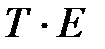) и расчет значений Т с использованием полученного уравнения тренда;

­ расчет полученных по модели значений ( 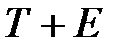) или ( );

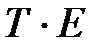­ расчет абсолютных и относительных ошибок.

Другой метод моделирования временного ряда, содержащего сезонные изменения, состоит в построении модели регрессии с включением фактора времени и фиктивных переменных. Количество фиктивных переменных должно быть на единицу меньше числа периодов внутри одного цикла колебаний. Например, при моделировании поквартальных данных модель должна включать 4 независимые переменные – фактор времени и 3 фиктивные переменные. Она равна единице для данного периода и нулю для всех остальных периодов, т.е.

,

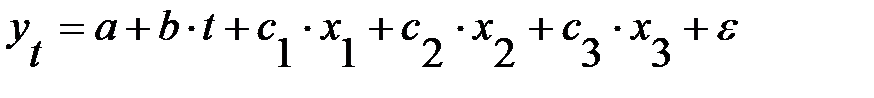где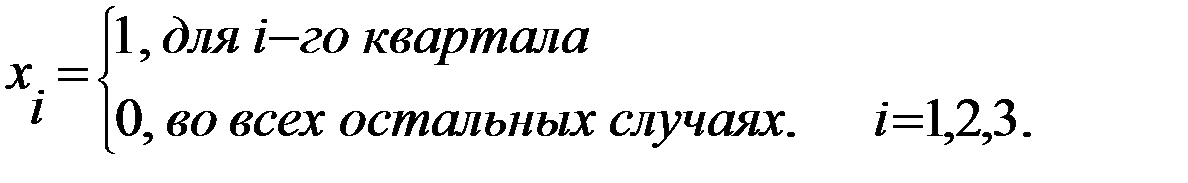

В основе экстрополяционных методов прогнозирования лежит предположение о том, что основные факторы и тенденции, имевшие место в прошлом, сохраняются в будущем.

При краткосрочном прогнозировании, а также при прогнозировании в ситуации изменения внешних условий, когда более важными являются последние реализации исследуемого процесса, более эффективными оказываются адаптивные методы, учитывающие неравноценность уровней временного ряда.

Адаптивные модели прогнозирования – это модели дисконтирования данных, способные быстро приспосабливать свою структуру и параметры к изменению условий. Инструментом прогноза в адаптивной модели является математическая модель, аргументом которой выступает – время.

При оценке параметров адаптивных моделей, в отличии от «кривых роста», наблюдениям (уровням ряда) присваиваются различные веса, в зависимости от того, насколько сильным признается их влияние на текущий уровень. Это позволяет учитывать изменения в тенденции, а также любые колебания, в которых прослеживается закономерность.

В качестве примера рассмотрим модель экспоненциального сглаживания Брауна. Модель Брауна может отображать развитие не только в виде линейной тенденции, или в виде случайного процесса, не имеющего тенденции.

Соответственно различают модели Брауна:

­ нулевого порядка, которая описывает процессы, не имеющие тенденции развития. Она содержит один параметр А₀;

­ первого порядка ( 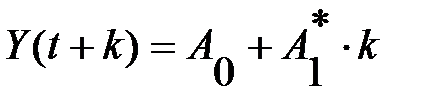), отражающей тенденцию в виде прямой линии;

­ второго порядка, отражающей развитие в виде параболической тенденции с «ускорением». Прогноз осуществляется по формуле: .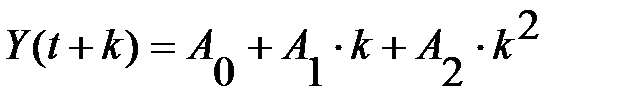

Порядок модели определяют обычно либо априорно на основе визуального анализа графика процесса, либо методом проб, сравнивая статистические характеристики моделей различного порядка на участке прогнозирования.

Рассмотрим этапы построения линейной модели Брауна:

Этап 1. По первым пяти точкам временного ряда оцениваются начальные значения А₀ и A₁ с помощью МНК:

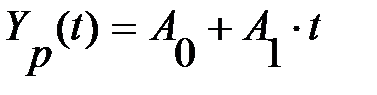(t=1,2,3,4,5).

Этап 2. С использованием полученного уравнения рассчитывают прогноз на один шаг (к=1)

.

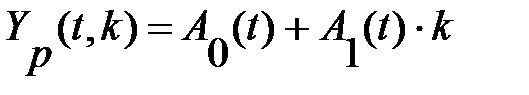Этап 3. Вычисляется величина расхождения расчетного значения с фактическим :

,

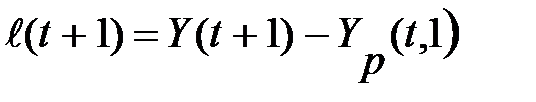где Y(t+1) – фактическое значение экономического показателя.

Этап 4. В соответствии с этой величиной корректируются параметры модели:

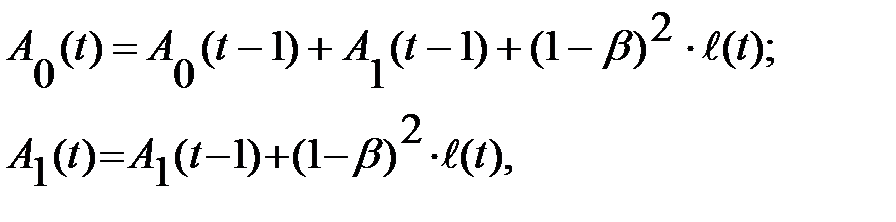
где 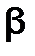- коэффициент дисконтирования данных( ).

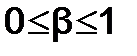Обычно полагают

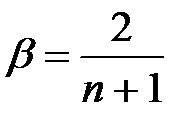, где n - длина временного ряда,

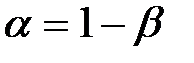- называют параметром сглаживания.

Этап 5. По модели со скорректированными параметрами A₀ и A₁ находят прогноз на следующий момент времени. Если t<N, то возврат на пункт 3 если t=N, то модель можно использовать для прогнозирования.

Этап 6. Строится интервальный прогноз.

В авторегрессионых моделях текущее значение процесса представляется как линейная комбинация предыдущих его значений и случайной компоненты.