Понятие о системах эконометрических уравнений
Многие экономические взаимосвязи допускают моделирование одним уравнением, но при анализе сложных экономических систем использование отдельных уравнений регрессии является иногда очень грубым предположением: практически изменение одной переменной, как правило, не может происходить при абсолютной неизменности других.
Например, при оценке эффективности производства нельзя руководствоваться только моделью рентабельности. Она должна быть дополнена моделью производительности труда, а также моделью себестоимости единицы продукции.
Поэтому в последние десятилетия в экономических исследованиях важное место заняла проблема описания структуры связей между переменными, системой, так называемых одновременных уравнений, называемых также структурными уравнениями.
Система уравнений в эконометрических исследованиях может быть построена по-разному.

Возможна система независимых уравнений, когда каждая зависимая переменная (у) рассматривается как функция одного и того же набора факторов:
Набор факторов хi в каждом уравнении может варьироваться, например:
у 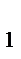 =f(х
=f(х 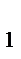 ,х
,х 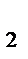 ,х
,х  ,х
,х  ,х
,х  ), у
), у 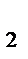 = f(х
= f(х 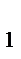 ,х
,х  ,х
,х  ,), у
,), у  = f(х
= f(х 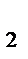 ,х
,х  ,х
,х  ), у
), у  = f(х
= f(х  ,х
,х  ) и т.д.
) и т.д.
Для определения параметров каждого, отдельно взятого уравнения, используется МНК.
Если зависимая переменная у одного уравнения выступает в качестве фактора х в другом уравнении, то получаем систему рекурсивных уравнений:

Параметры каждого уравнения данной системы также определяются обычным МНК.
Наибольшее распространение в эконометрических исследованиях получили системы взаимозависимых уравнений, в которых одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую часть системы:

Такие системы называют также системами совместных, одновременных уравнений. В отличие от предыдущих систем, каждое уравнение данной системы не может рассматриваться самостоятельно. Поэтому для определения параметров этой системы традиционный МНК не приемлем, а используются специальные методы.
Система совместных, одновременных уравнений (которая также называется структурной формой модели) обычно содержит эндогенные и экзогенные переменные. Эндогенные (зависимые) переменные в приведенной ранее системе обозначены как у. Их число равно числу уравнений в системе.
Экзогенные (независимые) переменные, это переменные, влияющие на эндогенные переменные, но не зависящие от них. Обозначаются обычно как х.
Простейшая структурная форма модели имеет вид:

Коэффициенты b  и
и 
 - называются структурными коэффициентами модели.
- называются структурными коэффициентами модели.
Если пользоваться МНК для оценки структурных коэффициентов модели, то получаются смещенные и несостоятельные оценки. Поэтому для определения структурных коэффициентов модели необходимо: структурную форму модели преобразовать в приведенную форму, которая имеет вид:

где 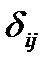 - коэффициенты приведенной формы модели.
- коэффициенты приведенной формы модели.
По своему виду приведенная форма является системой независимых уравнений, поэтому для оценки 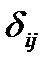 можно применить МНК, а затем оценить структурные коэффициенты модели.
можно применить МНК, а затем оценить структурные коэффициенты модели.
Процесс преобразования структурной формы в приведенную рассмотрим на примере. Пусть задана система одновременных уравнений:
 (4.1)
(4.1)
Приведенная форма модели для (1) имеет вид: 
 (4.2)
(4.2)
Из первого уравнения системы (4.1) получаем:
у 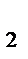 =(у
=(у 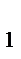 -
- 
 х
х 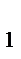 )/ b
)/ b