Тема 1. Предмет, задачи, критерии и принципы эконометрики

Содержание

Введение.. 5

Тема 1. Предмет, задачи, критерии и принципы эконометрики.. 8

1.1. Предмет и задачи курса. 8

1.2. Особенности эконометрического анализа. 9

1.3. Измерения в экономике. 10

Тема 2. Корреляционный и регрессионный анализ – математический метод оценки взаимосвязей экономических явлений.. 11

2.1. Парная регрессия и корреляция в эконометрических исследованиях.. 11

2.1.1. Модель парной регрессии. Спецификация модели.. 11

2.1.2. Линейная регрессия сущность, оценка параметров. 14

2.1.3. Определение тесноты связи и оценка существенности уравнения регрессии 15

2.2. Нелинейная регрессия в экономике и ее линеаризация. 18

2.2.1. Виды нелинейных регрессионных моделей, расчет их параметров. 18

2.2.2. Оценка корреляции для нелинейной регрессии.. 20

2.3. Множественная регрессия и корреляция. 23

2.3.1. Множественная регрессия. Отбор факторов при построении ее модели. 23

2.3.2. Расчет параметров и характеристик модели множественной регрессии 25

2.3.3. Частные уравнения множественной регрессии. Индексы множественной и частной корреляции и их расчет... 28

2.3.4. Обобщённый метод наименьших квадратов. Гомоскедастичность и гетероскедастичность. 32

Тема 3. Информационные технологии в эконометрических исследованиях 36

Тема 4. Системы эконометрических уравнений.. 41

4.1. Понятие о системах эконометрических уравнений.. 41

4.2. Проблема идентификации модели.. 43

4.3. Методы оценки параметров одновременных уравнений.. 44

Тема 5. Методы и модели анализа динамики экономических процессов.. 47

5.1. Понятие экономических рядов динамики. Сглаживание временных рядов. 47

5.2. Автокорреляционная функция. Коррелограмма. 51

5.3. Автокорреляция в остатках. Критерий Дарбина-Уотсона. 52

5.4. Моделирование тенденций временного ряда. Адаптивные модели прогнозирования 55

Тема 6. Макро- и региональные эконометрические модели.. 58

6.1. Макроэконометрические модели.. 58

6.2. Сущность и особенности региональных эконометрических моделей.. 60

6.3. Филадельфийская модель региональной экономики.. 62

Тема 7. Моделирование динамических процессов.. 64

7.1. Характеристика моделей с распределенным лагом и моделей авторегрессии.. 64

7.2. Выбор вида модели с распределительным лагом.. 66

7.3. Модели адаптивных ожиданий и неполной корректировки.. 69

Приложения.. 72

1. Базовые понятия теории вероятностей.. 72

1.1. Вероятность. Случайная величина.. 72

1.2. Числовые характеристики случайных величин.. 74

1.3. Законы распределений случайных величин.. 75

2. Базовые понятия статистики.. 76

2.1. Генеральная совокупность и выборка.. 76

2.2. Вычисление выборочных характеристик.. 77

3.Статистические выводы: оценки и проверка гипотез. 78

4. Статистическая проверка гипотез. 80

Литература.. 82

Введение

Современная экономическая теория, как на микро, так и на макро уровне, постоянно усложняющиеся экономические процессы привели к необходимости создания и совершенствования особых методов изучения и анализа. При этом широкое распространение получило использование моделирования и количественного анализа. На базе последних выделилось и сформировалось одно из направлений экономических исследований – эконометрика.

Эконометрика как наука расположена где–то между экономикой, статистикой и математикой, но ни одно из этих наук неспособна в отдельности, заменить эконометрику.

К основным задачам эконометрики можно отнести следующие:

- построение эконометрических моделей, то есть представление экономических моделей в математической форме. Данную проблему принято называть проблемой спецификации.

- оценка параметров построенной модели. Это этап параметризации.

- проверка качества найденных параметров модели и самой модели в целом. Иногда этот этап называют верификаций.

- использование построенных моделей для объяснения поведения исследуемых экономических показателей, прогнозирования и предсказания.

Эконометрические модели и методы сейчас – это не только мощный инструментарий для получения новых знаний в экономике, но и широко применяемый аппарат для принятия практических решений в прогнозировании, банковском деле, бизнесе. Развитие информационных технологий и специальных прикладных программ, совершенствование методов анализа сделали эконометрику мощнейшим инструментом экономических исследований.

Модели

Одно из определений эконометрики может звучать так: это наука, связанная с эмпирическим выводом экономических законов. То есть мы используем наблюдаемые значения или данные для того, чтобы получить количественные зависимости для экономических соотношений.

Но это – только малая часть задач, решаемых эконометрикой. Она также позволяет формулировать экономические модели, основываясь на эмпирических данных, оценивать неизвестные величины (параметры) в этих моделях, делать прогнозы и дает рекомендации по экономической политике.

В эконометрических исследованных существенным является использование моделей. Модели должны быть “настолько простыми, насколько возможно, но не проще”, сказал Эйнштейн.

Рассмотрим пример.

Пусть необходимо проанализировать зависимость спроса Q на некоторый товар от цены P на этот товар. На основе экономической теории известно, что с ростом цены объем спроса сокращается. Опираясь на это утверждение можно предложить несколько математических зависимостей, отражающих этот факт. Например,

Необходимо отметить, что любая из моделей будет лишь упрощением реальности и всегда содержит определенную погрешность. Поэтому из всех предлагаемых моделей с помощью статистических методов отбирается та, которая в наибольшей степени соответствует реальным эмпирическим данным и характеру зависимости.

Далее идет этап параметризации, то есть оценка параметров (в нашем случае α и β ) так как эта оценка осуществляется на основе имеющихся статистических данных, то вопрос точности (качества ) статистической информации является одним из ключевых при построении модели.

Затем проверяется качество найденных оценок, а также соответствие модели эмпирическим данным и теоретическим предпосылкам (этап верификации ). Данный анализ в основном осуществляется по схеме проверки статистических гипотез. На этом этапе совершенствуется не только форма модели, но и уточняется состав ее объясняющих переменных (возможно спрос на товар определяется не только его ценой, но и другими факторами, например, располагаемым доходом).

Если модель удовлетворяет требованиям качества, то она может быть использована для прогнозирования, либо для анализа внутреннего механизма исследуемых процессов.

Математические модели широко применяются в бизнесе, экономике, общественных науках, исследовании экономической активности.

Математические модели позволяют более полно исследовать и понимать сущность происходящих процессов, анализировать их.

В эконометрических исследованиях используют разные типы моделей. Но можно выделить три основных класса моделей, которые применяются в эконометрике: модели временных рядов, регрессионные модели ( с одним уравнением) и системы одновременных уравнений.

Типы данных

В эконометрических исследованиях используют два типа данных: пространственные данные (cross – sectional data) и временные ряды(time – series data).

Пространственные данные – это данные, по какому- либо экономическому показателю, полученные для разных однотипных объектов (фирм, компаний, регионов ).

Временные ряды – это данные, характеризующие один и тот же объект, но в различные моменты времени.

Примерами пространственных данных являются, например, объем производства, количество работников, прибыль и т.д. по разным предприятиям в один и тот же момент времени (пространственный срез).

Примерами временных рядов могут быть, например, ежеквартальные данные по прибыльности, объему выпускаемой продукции, средней заработной плате и т.д. для отдельного предприятия.

Предмет и задачи курса

На современном этапе экономического развития - деятельность в любой сфере (управлении, финансово-кредитной сфере, маркетинге, учете, аудите) требует от специалиста умения применить современные методы работы, знания достижений мировой экономической мысли, понимания научного языка. Большинство новых методов основано на эконометрических моделях, концепциях, приемах. Без глубоких знаний экономики научиться их использовать невозможно. Хорошая эконометрическая подготовка необходима также и для чтения современной экономической литературы.

Специфической особенностью деятельности экономиста является работа в условиях неопределенности: недостатка информации и неполноты исходных данных. Для анализа такой информации требуются специальные методы, составляющие один из аспектов эконометрики. Центральной проблемой эконометрики является построение экономической модели и определение возможностей ее использования для описания, анализа и прогнозирования реальных экономических процессов.

Известный экономист Цви Гриллихес (1929-1999) писал: « Эконометрика является одновременно нашим телескопом и нашим микроскопом для изучения окружающего экономического мира».

Свидетельством всемирного признания эконометрики является присуждение Нобелевских премий за разработки в эконометрической области в 1969 г. Р.Фришу и Я.Тинбергену за разработку математических методов анализа экономических процессов; в 1980 – Л. Клейну за создание эконометрических моделей и их применение к анализу экономических колебаний и экономической политике; в 1989 г. – Т. Хаавельмо за прояснение вероятностных основ эконометрики и анализ одновременных экономических структур; в 2000 г.– Дж. Хекману за развитие теории и методов анализа селективных выборок и

Д. Макфаддену за развитие теории и методов анализа моделей дискретного выбора.

Эконометрика – быстроразвивающаяся отрасль науки, цель которой состоит в том, чтобы придать количественные меры экономическим отношениям.

Термин «эконометрика» был впервые введен бухгалтером П. Цьемпой (Австро-Венгрия, 1910 г.) («эконометрия» - у Цьемпы).

Слово «эконометрика» представляет собой комбинацию двух слов: «экономика» и «метрика», выражая таким образом, специфику, содержание эконометрики как науки: количественное выражение тех связей и соотношений, которые раскрыты и обоснованны экономической теорией.

Это новое научное направление возникло на стыке трех наук: экономической теории, статистики и математики. На дальнейшее развитие эконометрики большое воздействие оказывают новые информационные технологии.

Эконометрика входит в комплекс дисциплин «Экономико - математические методы». Ёе предметом является количественное выражение взаимосвязей и зависимостей экономических явлений и процессов, закономерностей экономики.

Первые попытки количественных исследований в экономике относятся к 17 веку. Однако эконометрика как наука сформировалась лишь в 20 – веке.

29 декабря 1930 г. по инициативе И. Фишера, Р.Фицера, Я. Тинбергена и др. на заседании Американской ассоциации развития науки было создано эконометрическое общество, на котором новой науке дали название – «эконометрика». В 1941 году появился первый учебник по эконометрике, который был создан Я.Тинбергеном.

Измерения в экономике

Понятие «эконометрика» включает экономические измерения.

Признаками измерения называют, прежде всего, получение, сравнение и упорядочение информации. Это определение исходит из того, что измерение предполагает выделение некоторого свойства, по которому производится сравнение объектов в определенном отношении.

Другое понимание измерения исходит из числового выражения результата, т.е. измерение трактуется как операция, в результате которой получается численное значение величины.

Третий подход к измерению связан с обязательным наличием единицы измерения (эталона).

Любому измерению предшествует качественный анализ, учитывающий цели исследования качественный анализ необходим и после выполнения измерения.

Специфика экономических измерений состоит в наличии большого числа разнородных данных – разнородных ресурсов, разнородных результатов (например, товаров и услуг).

Нередко в экономических измерениях возникает задача отражения иерархии измерителей, которая выражается в выделении интегрального и частных показателей.

Точность измерения – это его адекватность.

Для социально экономических измерений характерны специфические представления о точности. Экономику относят к неточным наукам, т.к. невозможно провести измерение с произвольно малой погрешностью.

По объективным причинам для социально-экономических измерений характерна низкая контролируемость их точности.

Основной базой данных для эконометрических исследований служат данные официальной статистики либо данные бухгалтерского учета. Т. о., проблемы экономического измерения – это проблемы статистики и учета.

Если в естественных науках большей частью имеют дело со строгими (функциональными) зависимостями, при которых каждому значению одной переменной соответствует единственное значение другой, то между экономическими переменными, в большинстве случаев, таких зависимостей нет. Поэтому в экономике имеют дело с корреляционными зависимостями.

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая регрессия представляет собой регрессию между двумя переменными y и x, т.е. модель вида

y = f(x),

где у – зависимая переменная (результативный признак); х – независимая, или объясняющая, переменная, (признак – фактор).

Обычно полагают

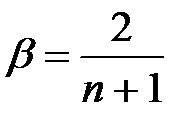, где n - длина временного ряда,

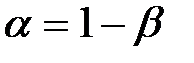- называют параметром сглаживания.

Этап 5. По модели со скорректированными параметрами A₀ и A₁ находят прогноз на следующий момент времени. Если t<N, то возврат на пункт 3 если t=N, то модель можно использовать для прогнозирования.

Этап 6. Строится интервальный прогноз.

В авторегрессионых моделях текущее значение процесса представляется как линейная комбинация предыдущих его значений и случайной компоненты.

Модели адаптивных ожиданий.

Рассмотрим модель вида

, (7.13)

где у - фактическое значение результативного признака;

- ожидаемое значение факторного признака.

Механизм формирования ожиданий в этой модели следующий:

или (7.14)

где 0< <1, х - фактическое значение.

Из (7.14) следует, что в каждый период времени t+1 ожидания корректируются на некоторую долю . Параметр называется коэффициентом ожиданий.

Чем ближе к 1, тем в большей степени реализуются ожидания экономических агентов. И, если приближается к 0, то это свидетельствует об устойчивости существующих тенденций.

Если выражение (7.14) подставить в (7.13), то получим

(7.15)

На основе (7.15) для периода (t-1) можно получить:

(7.16)

Умножив (7.16) на (1- ) и вычитывая из (7.15) можно получить

, (7.17)

где U = .

Т.о. получили модель авторегрессии, определив параметры которой можно легко перейти к исходной модели (7.17).

Модель (7.17) включает только фактические значения переменных ( ).

Модель (7.13) называется долгосрочной функцией модели адаптивных ожиданий. Модель (7.17) – краткосрочной функцией модели адаптивных ожиданий.

Модель неполной корректировки. В модели неполной корректировки предполагается, что уравнение определяет не фактическое значение зависимой переменной у_t, а ее ожидаемый (желаемый) уровень

(7.18)

Предполагается, что фактическое приращение зависимой переменной (у -у ) пропорционально разнице между ее желаемым уровнем и значением в предыдущий период,

(y -y ) =

Откуда (7.19)

Т.о., фактическое значение результата текущего периода у_t есть средняя арифметическая взвешенная его ожидаемого значения текущего периода и фактического значения за предыдущий период времени у . Чем больше значение , тем быстрее происходит процесс корректировки. Если =1, то и полная корректировка происходит за один период. Если =0, то корректировка не происходит вообще.

Подставляя уравнение (7.18) в найденное выражение (7.19), можно получить:

, (7.20)

где U = .

Соотношение (7.20) есть основное уравнение модели неполной корректировки.

Легко заметить, что уравнение (7.20) включает только фактические значения переменных. Зная оценки параметров этого уравнения, можно определить . Затем путем алгебраических преобразований рассчитываются параметры и уравнения (7.18). Уравнение (7.18) называют также долгосрочной функцией модели неполной корректировки.

Описанные выше: преобразования Койка, модели адаптивных ожиданий и неполной корректировки, сводятся к модели авторегрессии. Однако при построении моделей авторегрессии возникают две серьезные проблемы:

- проблема, выбора метода, оценки параметров уравнения авторегрессии. Наличие лаговых значений результативного признака приводит к нарушению предпосылки МНК о делении переменных на результативную и факторные;

- т.к. в модели авторегрессии существует зависимость между текущими значениями результата y_t и текущими значениями остатков U_t, то нарушается предпосылка МНК об отсутствии связи между факторным признаком и остатками в уравнении регрессии.

Поэтому применение обычного МНК для оценки параметров уравнения авторегрессии приводит к получению смещенной оценки параметра при переменной у_t-1.

Один из методов расчета параметров уравнения авторегрессии является метод инструментальных переменных. Сущность метода состоит в том, чтобы заменить переменную из правой части модели, для которой нарушаются предпосылки МНК, на новую переменную, для которой предпосылки не нарушаются. Для моделей авторегрессии необходимо удалить из правой части модели переменную y_t-1. Новая переменная, которая будет введена должна иметь два свойства:

­ должна тесно коррелировать с у_t-1;

­ не должна коррелировать с остатками U_t.

Так как в модели авторегрессии переменная у_t зависит не только от у_t-1, но и от х_t, то можно предположить, что имеет место зависимость у_t-1 от х_t-1, т.е.

.

Откуда получаем, что

,

где . (7.21)

Т.о., оценки параметров уравнения авторегрессии можно найти из соотношения:

,

предварительно определив значения по уравнению (7.21).

Содержание

Введение.. 5

Тема 1. Предмет, задачи, критерии и принципы эконометрики.. 8

1.1. Предмет и задачи курса. 8

1.2. Особенности эконометрического анализа. 9

1.3. Измерения в экономике. 10

Тема 2. Корреляционный и регрессионный анализ – математический метод оценки взаимосвязей экономических явлений.. 11

2.1. Парная регрессия и корреляция в эконометрических исследованиях.. 11

2.1.1. Модель парной регрессии. Спецификация модели.. 11

2.1.2. Линейная регрессия сущность, оценка параметров. 14

2.1.3. Определение тесноты связи и оценка существенности уравнения регрессии 15

2.2. Нелинейная регрессия в экономике и ее линеаризация. 18

2.2.1. Виды нелинейных регрессионных моделей, расчет их параметров. 18

2.2.2. Оценка корреляции для нелинейной регрессии.. 20

2.3. Множественная регрессия и корреляция. 23

2.3.1. Множественная регрессия. Отбор факторов при построении ее модели. 23

2.3.2. Расчет параметров и характеристик модели множественной регрессии 25

2.3.3. Частные уравнения множественной регрессии. Индексы множественной и частной корреляции и их расчет... 28

2.3.4. Обобщённый метод наименьших квадратов. Гомоскедастичность и гетероскедастичность. 32

Тема 3. Информационные технологии в эконометрических исследованиях 36

Тема 4. Системы эконометрических уравнений.. 41

4.1. Понятие о системах эконометрических уравнений.. 41

4.2. Проблема идентификации модели.. 43

4.3. Методы оценки параметров одновременных уравнений.. 44

Тема 5. Методы и модели анализа динамики экономических процессов.. 47

5.1. Понятие экономических рядов динамики. Сглаживание временных рядов. 47

5.2. Автокорреляционная функция. Коррелограмма. 51

5.3. Автокорреляция в остатках. Критерий Дарбина-Уотсона. 52

5.4. Моделирование тенденций временного ряда. Адаптивные модели прогнозирования 55

Тема 6. Макро- и региональные эконометрические модели.. 58

6.1. Макроэконометрические модели.. 58

6.2. Сущность и особенности региональных эконометрических моделей.. 60

6.3. Филадельфийская модель региональной экономики.. 62

Тема 7. Моделирование динамических процессов.. 64

7.1. Характеристика моделей с распределенным лагом и моделей авторегрессии.. 64

7.2. Выбор вида модели с распределительным лагом.. 66

7.3. Модели адаптивных ожиданий и неполной корректировки.. 69

Приложения.. 72

1. Базовые понятия теории вероятностей.. 72

1.1. Вероятность. Случайная величина.. 72

1.2. Числовые характеристики случайных величин.. 74

1.3. Законы распределений случайных величин.. 75

2. Базовые понятия статистики.. 76

2.1. Генеральная совокупность и выборка.. 76

2.2. Вычисление выборочных характеристик.. 77

3.Статистические выводы: оценки и проверка гипотез. 78

4. Статистическая проверка гипотез. 80

Литература.. 82

Введение

Современная экономическая теория, как на микро, так и на макро уровне, постоянно усложняющиеся экономические процессы привели к необходимости создания и совершенствования особых методов изучения и анализа. При этом широкое распространение получило использование моделирования и количественного анализа. На базе последних выделилось и сформировалось одно из направлений экономических исследований – эконометрика.

Эконометрика как наука расположена где–то между экономикой, статистикой и математикой, но ни одно из этих наук неспособна в отдельности, заменить эконометрику.

К основным задачам эконометрики можно отнести следующие:

- построение эконометрических моделей, то есть представление экономических моделей в математической форме. Данную проблему принято называть проблемой спецификации.

- оценка параметров построенной модели. Это этап параметризации.

- проверка качества найденных параметров модели и самой модели в целом. Иногда этот этап называют верификаций.

- использование построенных моделей для объяснения поведения исследуемых экономических показателей, прогнозирования и предсказания.

Эконометрические модели и методы сейчас – это не только мощный инструментарий для получения новых знаний в экономике, но и широко применяемый аппарат для принятия практических решений в прогнозировании, банковском деле, бизнесе. Развитие информационных технологий и специальных прикладных программ, совершенствование методов анализа сделали эконометрику мощнейшим инструментом экономических исследований.

Модели

Одно из определений эконометрики может звучать так: это наука, связанная с эмпирическим выводом экономических законов. То есть мы используем наблюдаемые значения или данные для того, чтобы получить количественные зависимости для экономических соотношений.

Но это – только малая часть задач, решаемых эконометрикой. Она также позволяет формулировать экономические модели, основываясь на эмпирических данных, оценивать неизвестные величины (параметры) в этих моделях, делать прогнозы и дает рекомендации по экономической политике.

В эконометрических исследованных существенным является использование моделей. Модели должны быть “настолько простыми, насколько возможно, но не проще”, сказал Эйнштейн.

Рассмотрим пример.

Пусть необходимо проанализировать зависимость спроса Q на некоторый товар от цены P на этот товар. На основе экономической теории известно, что с ростом цены объем спроса сокращается. Опираясь на это утверждение можно предложить несколько математических зависимостей, отражающих этот факт. Например,

Необходимо отметить, что любая из моделей будет лишь упрощением реальности и всегда содержит определенную погрешность. Поэтому из всех предлагаемых моделей с помощью статистических методов отбирается та, которая в наибольшей степени соответствует реальным эмпирическим данным и характеру зависимости.

Далее идет этап параметризации, то есть оценка параметров (в нашем случае α и β ) так как эта оценка осуществляется на основе имеющихся статистических данных, то вопрос точности (качества ) статистической информации является одним из ключевых при построении модели.

Затем проверяется качество найденных оценок, а также соответствие модели эмпирическим данным и теоретическим предпосылкам (этап верификации ). Данный анализ в основном осуществляется по схеме проверки статистических гипотез. На этом этапе совершенствуется не только форма модели, но и уточняется состав ее объясняющих переменных (возможно спрос на товар определяется не только его ценой, но и другими факторами, например, располагаемым доходом).

Если модель удовлетворяет требованиям качества, то она может быть использована для прогнозирования, либо для анализа внутреннего механизма исследуемых процессов.

Математические модели широко применяются в бизнесе, экономике, общественных науках, исследовании экономической активности.

Математические модели позволяют более полно исследовать и понимать сущность происходящих процессов, анализировать их.

В эконометрических исследованиях используют разные типы моделей. Но можно выделить три основных класса моделей, которые применяются в эконометрике: модели временных рядов, регрессионные модели ( с одним уравнением) и системы одновременных уравнений.

Типы данных

В эконометрических исследованиях используют два типа данных: пространственные данные (cross – sectional data) и временные ряды(time – series data).

Пространственные данные – это данные, по какому- либо экономическому показателю, полученные для разных однотипных объектов (фирм, компаний, регионов ).

Временные ряды – это данные, характеризующие один и тот же объект, но в различные моменты времени.

Примерами пространственных данных являются, например, объем производства, количество работников, прибыль и т.д. по разным предприятиям в один и тот же момент времени (пространственный срез).

Примерами временных рядов могут быть, например, ежеквартальные данные по прибыльности, объему выпускаемой продукции, средней заработной плате и т.д. для отдельного предприятия.

Тема 1. Предмет, задачи, критерии и принципы эконометрики

Предмет и задачи курса

На современном этапе экономического развития - деятельность в любой сфере (управлении, финансово-кредитной сфере, маркетинге, учете, аудите) требует от специалиста умения применить современные методы работы, знания достижений мировой экономической мысли, понимания научного языка. Большинство новых методов основано на эконометрических моделях, концепциях, приемах. Без глубоких знаний экономики научиться их использовать невозможно. Хорошая эконометрическая подготовка необходима также и для чтения современной экономической литературы.

Специфической особенностью деятельности экономиста является работа в условиях неопределенности: недостатка информации и неполноты исходных данных. Для анализа такой информации требуются специальные методы, составляющие один из аспектов эконометрики. Центральной проблемой эконометрики является построение экономической модели и определение возможностей ее использования для описания, анализа и прогнозирования реальных экономических процессов.

Известный экономист Цви Гриллихес (1929-1999) писал: « Эконометрика является одновременно нашим телескопом и нашим микроскопом для изучения окружающего экономического мира».

Свидетельством всемирного признания эконометрики является присуждение Нобелевских премий за разработки в эконометрической области в 1969 г. Р.Фришу и Я.Тинбергену за разработку математических методов анализа экономических процессов; в 1980 – Л. Клейну за создание эконометрических моделей и их применение к анализу экономических колебаний и экономической политике; в 1989 г. – Т. Хаавельмо за прояснение вероятностных основ эконометрики и анализ одновременных экономических структур; в 2000 г.– Дж. Хекману за развитие теории и методов анализа селективных выборок и

Д. Макфаддену за развитие теории и методов анализа моделей дискретного выбора.

Эконометрика – быстроразвивающаяся отрасль науки, цель которой состоит в том, чтобы придать количественные меры экономическим отношениям.

Термин «эконометрика» был впервые введен бухгалтером П. Цьемпой (Австро-Венгрия, 1910 г.) («эконометрия» - у Цьемпы).

Слово «эконометрика» представляет собой комбинацию двух слов: «экономика» и «метрика», выражая таким образом, специфику, содержание эконометрики как науки: количественное выражение тех связей и соотношений, которые раскрыты и обоснованны экономической теорией.

Это новое научное направление возникло на стыке трех наук: экономической теории, статистики и математики. На дальнейшее развитие эконометрики большое воздействие оказывают новые информационные технологии.

Эконометрика входит в комплекс дисциплин «Экономико - математические методы». Ёе предметом является количественное выражение взаимосвязей и зависимостей экономических явлений и процессов, закономерностей экономики.

Первые попытки количественных исследований в экономике относятся к 17 веку. Однако эконометрика как наука сформировалась лишь в 20 – веке.

29 декабря 1930 г. по инициативе И. Фишера, Р.Фицера, Я. Тинбергена и др. на заседании Американской ассоциации развития науки было создано эконометрическое общество, на котором новой науке дали название – «эконометрика». В 1941 году появился первый учебник по эконометрике, который был создан Я.Тинбергеном.