Методические указания к лабораторным работам
5.1. Описание рабочей программы
5.1.1. Общее описание программы
Программа Poisk предназначена для исследования различных алгоритмов поиска. После пуска рабочее окно программы показано на рис. 3. В верхней части окна расположены распахивающиеся списки для выбора распределения вероятностей событий (равномерное, экспоненциальное и определяемое вариантом задания от 1 до 15, номер варианта задается преподавателем), числа событий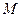 
(4, 8, 12, 16) и максимального числа измерений 
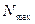(от 1 до 15). Ниже представлены выбранное распределение вероятностей 
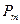и кривая снятия неопределенности (КСН).
В нижней части окна находится наборное поле, с помощью кнопок которого задается алгоритм поиска – нажатая кнопка означает, что при данном измерении проверяется наличие или отсутствие соответствующего события.
При последовательном поиске в каждом измерении может проверяться только одно событие, а при дихотомическом – любая группа событий.
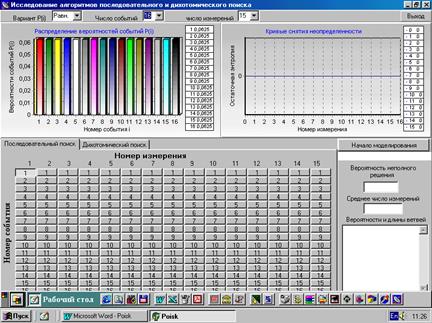
Рис..3
В правой нижней части окна расположена кнопка начала моделирования, под ним окно, в которое выводится сообщение о полноте выбранного алгоритма поиска, затем окна, в которых показываются вероятность неполного решения, среднее число измерений (алгоритмическая скрытность) и в самом низу – вероятности возникновения ветвей и их длина для дерева поиска.
Выбор последовательного или дихотомического алгоритма поиска осуществляется закладками блокнота в верхней части наборного поля.
5.1.2. Режим последовательного поиска
На рис. 4 представлено рабочее окно программы при исследовании алгоритма последовательного поиска для восьми событий (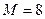 
) при равномерном распределении их вероятностей.
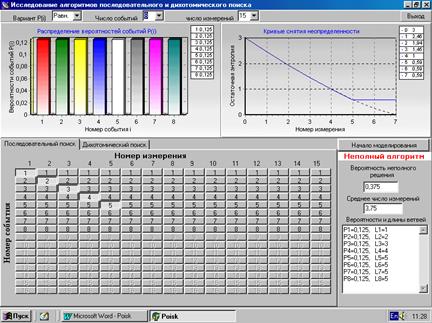
Рис. 4.
В программе сначала устанавливаются рабочие параметры, алгоритм поиска, а затем нажимается кнопка «Начало моделирования». Выбранный алгоритм поиска предполагает последовательный перебор событий, начиная с первого (номер
измерения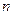 
равен номеру события 
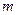). Алгоритм неполный (не проверяются события с номерами 6, 7 и 8). Это приводит к тому, что с вероятностью 0,375 решение принять нельзя, а КСН не достигает нулевого значения. На графике КСН пунктиром показана оптимальная (потенциальная) кривая, ниже которой КСН опускаться не может.
Дерево поиска определяется нажатыми кнопками наборного поля, а его параметры (вероятности ветвей и их длина) приведены в правом нижнем окне. По этим данным дерево поиска можно построить графически, как показано на рис. 5.
Как видно, не проверяются события из с номерами 6, 7 и 8. Алгоритм поиска можно дополнить двумя измерениями, и он станет полным, обеспечивающим проверку всех событий. При этом вероятность неполного решения станет равной нулю, а среднее число измерений увеличится.
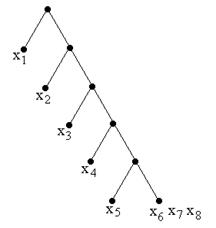
Рис. 5.
5.1.3. Режим дихотомического поиска
Рабочее окно программы в режиме дихотомического поиска показано на рис 6. Как видно, в каждом измерении про-
веряются несколько событий, образуя полный алгоритм поиска. Желтым цветом показаны ветви дерева поиска, полностью разделяющие события.
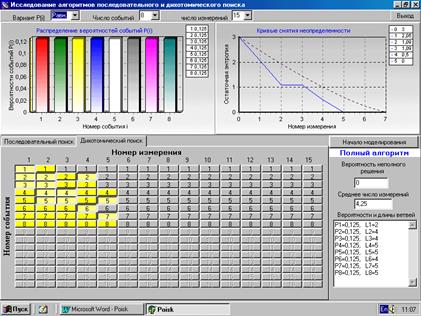
Рис. 6.
Если алгоритм неполный, то неразделяемые события не отмечаются желтым цветом, при нажатии кнопки «Начало моделирования» выдается сообщение «Неполный алгоритм» и расчет характеристик поиска не производится. В поле графиков КСН остается пунктирная кривая, соответствующая оптимальному последовательному алгоритму поиска при том же распределении вероятностей событий.
По нажатым кнопкам наборного поля можно построить дерево поиска, которое в примере, показанном на рис. 6, имеет вид рис. 7.
Как видно, третье измерение является полностью холостым, что и отражается на КСН горизонтальным участком.
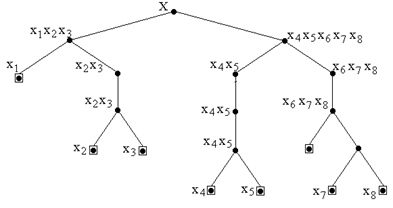
Рис. 7.
5.2. Лабораторная работа 1 «Исследование алгоритмов последовательного и дихотомического поиска»
Последовательный поиск
5.2.1. Установите равномерное распределение вероятностей событий при их числе 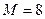для четного и 
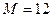для нечетного вариантов. Задайте максимальное число измерений 
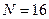. На наборном поле задайте полный алгоритм поиска «n=m», при котором номер события 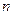равен номеру измерения 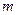(последнее событие не проверяется). Проведите моделирование, определите среднее число измерений 
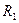. Результат внесите в табл. 2.
Таблица 2.
| |  |  | |
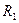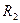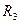| моделирование | |||
| расчет |
На наборном поле включите проверку последнего события, определите среднее число измерений 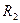, запишите его в табл. 2, проанализируйте результаты. Проведите расчет скрытностей 
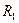и 
.
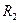Задайте алгоритм поиска «n=M-m+1», при котором первым проверяется последнее событие, а последним – второе (первое событие не проверяется). По результатам моделирования определите среднее число измерений 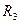, запишите его в табл. 2, проведите расчет 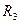, сделайте выводы.
5.2.2. Установите экспоненциальное распределение вероятностей событий (второе в распахивающемся списке) вида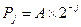 
, 
, 
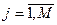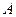- нормирующий множитель, при том же 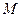, что и в пункте 6.2.1. На наборном поле установите алгоритм поиска «n=m» без проверки последнего события. Определите среднее число измерений 
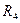, запишите его в табл. 3. Проведите расчет величины .
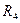Задайте алгоритм поиска «n=M-m+1» (первое событие не проверяется). По результатам моделирования найдите среднее число измерений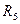 
, запищите его в табл. 3, проанализируйте результаты.
Таблица 3.
| | |
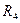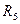5.2.3. Выберите из распахивающегося списка распределение вероятностей в соответствии со своим вариантом задания при числе событий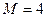 
. Пример рабочего окна показан на рис. 8.
Задайте алгоритм поиска «n=m» без проверки последнего события. Проведите моделирование. С помощью перехвата экрана «Print Screen» сохраните в отчете результаты работы.
Проанализируйте КСН, ее оптимальность, объясните ход кривой. Среднее число измерений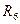 
внесите в табл. 4.
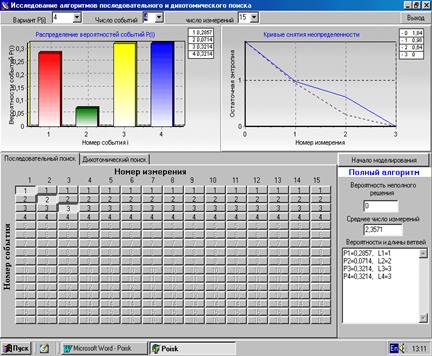Рис. 8.
Таблица 4.
| |  |  |  |
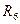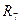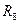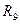5.2.4. Повторите эксперименты по пункту 6.2.3 для числа событий M=8, 12 и 16. Занесите в отчет результаты, значения среднего числа измерени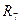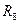й , и 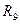запишите в табл. 3. Проведите сравнительный анализ.
Дихотомический поиск
5.2.5. Установите число событий 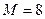для четного варианта и 
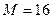для нечетного при равномерном распределении вероятностей и задайте число измерений 
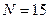. Временно включите режим последовательного поиска при алгоритме «n=m», проведите моделирование. Переключитесь в режим дихотомического поиска. В правой верхней части экрана останется график КСН последовательного поиска (пунктир).
Задайте с помощью наборного поля дихотомический алгоритм поиска, выполните моделирование. Проведите перехват экрана. Проанализируйте графики КСН для дихотомического и последовательного алгоритмов поиска.
5.2.6. Выберите экспоненциальное распределение вероятностей событий вида 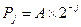, , 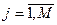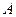- нормирующий множитель, при том же 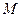, что и в пункте 6.2.5. Задайте дихотомический алгоритм поиска в этом случае. Проведите моделирование, проанализируйте результаты.
5.2.7. Выберите распределение вероятностей событий в соответствии с вариантом задания при 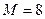. На наборном поле установите алгоритм дихотомического поиска. Проведите моделирование с последующим перехватом экрана.
Задайте алгоритм последовательного поиска «n=m», выполните моделирование с последующим перехватом экрана. Проанализируйте полученные результаты, сравните КСН рассмотренных алгоритмов поиска.
5.3. Лабораторная работа 2 «Оптимизация алгоритмов поиска»
5.3.1. Включите режим дихотомического поиска. Установите число событий 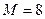для четного и 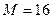для нечетного варианта при равномерном распределении вероятностей и задайте число измерений 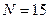. Разработайте опти-
мальный алгоритм поиска, задайте его на наборном поле, проведите моделирование, определите потенциальную скрытность. Проведите расчет потенциальной и энтропийной скрытностей, сравните результаты.
5.3.2. Выберите экспоненциальное распределение вероятностей событий вида 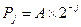, , 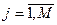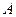- нормирующий множитель, при том же 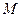, что и в пункте 5.3.1. Определите оптимальный алгоритм поиска, задайте его на наборном поле, проведите моделирование, определите потенциальную скрытность. Проведите сравнительный анализ результатов по пунктам 5.3.1 и 5.3.2.
5.3.3. Для экспоненциального распределения вероятностей из пункта 5.3.2 последовательно уменьшая максимальное число измерений от 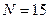до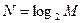 
, разработайте оптимальные алгоритмы поиска и по результатам моделирования определите соответствующие значения среднего числа измерений 
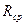. Результаты внесите в табл. 5.
Таблица 5.
| N | … | |||
| Rср |
Постройте график зависимости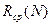 
. Проведите анализ результатов. Как изменяется оптимальный алгоритм поиска при ограничении максимального числа измерений.
5.3.4. Для своего варианта распределения вероятностей при числе событий 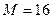разработайте оптимальный алгоритм поиска, постройте дерево поиска, объясните его форму, чем она обусловлена?
На наборном поле задайте оптимальный полный алгоритм поиска. Последовательно исключая последние измерения (до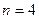 
), рассмотрите зависимость среднего числа измерений 
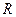, вероятности неполного решения 
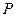и остаточной
скрытности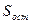 
от продолжительности поиска 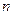. Результаты запишите в табл. 6, постройте графики. Проведите сравнительный анализ полученных результатов.
Таблица 6.
| n | … | ||||
| R | |||||
| P | |||||
| Sост |
ПРИЛОЖЕНИЕ А
Варианты распределения вероятностей
Таблица П1
| № | Распределение вероятностей | Значения параметров |
 ,  |   | |
 , |  | |
 , | | |
 , |  | |
 , | | |
 ,  |  | |
 ,  | |
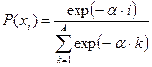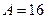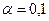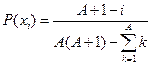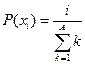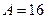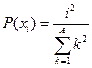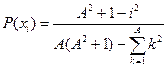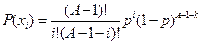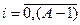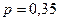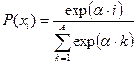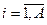Продолжение таблицы П1
 , |    | |
 , |  | |
 , |  | |
 , |  | |
 , |  | |
 , | | |
 , |  |
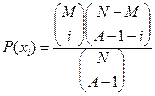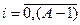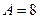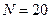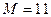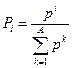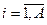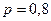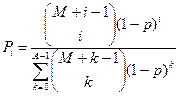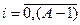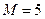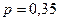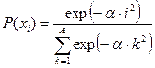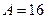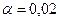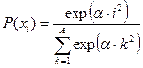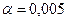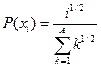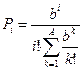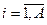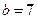Продолжение таблицы П1
 , |  | |
 , |  | |
 , | | |
 , | | |
 , | | |
 , |  | |
 , |  | |
 , | |
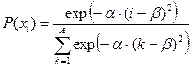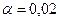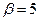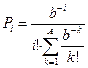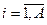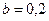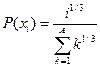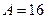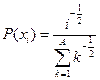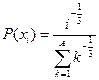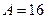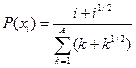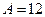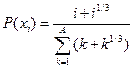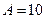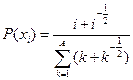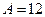Продолжение таблицы П1
 , |  | |
 , |  | |
| , |   | |
 , |  | |
 , |  | |
 , |   | |
 , |  | |
 , | |
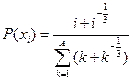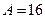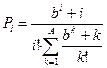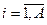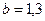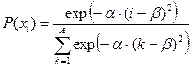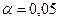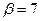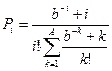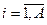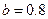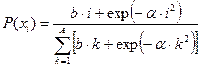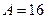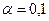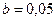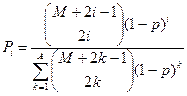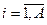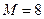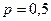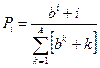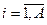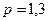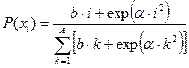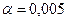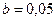Продолжение таблицы П1
 , |   | |
 , | | |
 , |   | |
 , |  | |
 , | | |
 , | | |
 , |  | |
 , | |
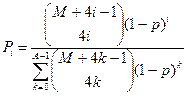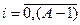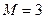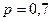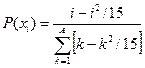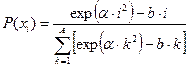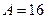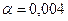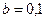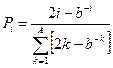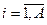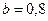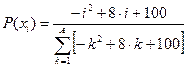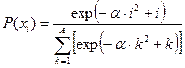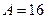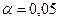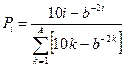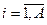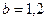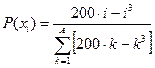ПРИЛОЖЕНИЕ Б
Пример программы для выполнения первого задания
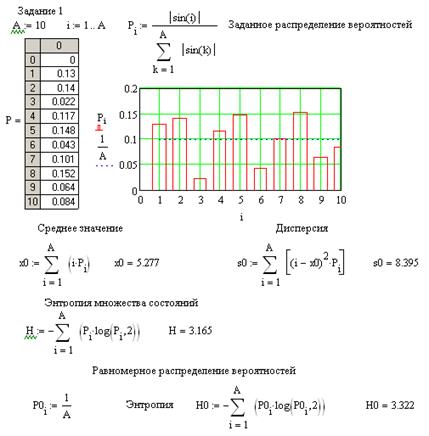
ПРИЛОЖЕНИЕ В
Биномиальные коэффициенты
В выражениях для распределения вероятностей (приложение А) используются биномиальные коэффициенты, равные
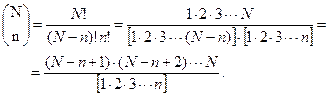
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Каневский З.М., Литвиненко В.П., Макаров Г.В., Максимов Д.А. Основы теории скрытности: Учеб. пособие/ Воронеж. гос. техн. ун-т. Воронеж, 2006. 202с.
2. Литвиненко В.П. Энергетическая скрытность сигналов и защищенность радиолиний. Учеб. пособие / Воронеж. гос. техн. ун-т. Воронеж, 2009. 166с.
3. Литвиненко В.П. Основы теории скрытности: практикум. Учеб. пособие / Воронеж. гос. техн. ун-т. Воронеж, 2010. 106с.
4. Палий А.И. Радиоэлектронная борьба. М., Связь, 1989, 430с..
5. Стандарт предприятия (СТП ВГТУ 005-2007). Дипломное проектирование. Оформление расчетно-пояснительной записки и графической части. Воронеж: ВГТУ, 2007. 34 с.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ ……………………………………….…..... 1
1. СОДЕРЖАНИЕ РАБОЧЕЙ ПРОГРАММЫ
ПРЕПОДАВАНИЯ ДИСЦИПЛИНЫ ……………… 1
2. СОДЕРЖАНИЕ РАЗДЕЛОВ ДИСЦИПЛИНЫ …… 3
3. СРЕДСТВА ОБЕСПЕЧЕНИЯ ОСВОЕНИЯ
ДИСЦИПЛИНЫ ……………….…………………..… 7
4. КОНТРОЛЬНАЯ РАБОТА ………………………….. 7
4.1. Общие методические указания …….……………… 7
4.2. Задание 1 «Энтропийная скрытность» ……...……. 7
4.3. Задание 2 «Последовательный поиск» …….......…. 8
4.4. Задание 3 «Дихотомический поиск» ……………… 9
4.5. Задание 4 «Оптимизация поиска» …..…………… 10
5. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К
ЛАБОРАТОРНЫМ РАБОТАМ ……………….….... 10
5.1. Описание рабочей программы ………..…………. 10
5.1.1. Общее описание программы …………………… 10
5.1.2. Режим последовательного поиска …………...… 12
5.1.3. Режим дихотомического поиска …….………… 13
5.2. Лабораторная работа 1 «Исследование
алгоритмов последовательного и дихотомичес-
кого поиска» …………………………………...…. 15
5.3. Лабораторная работа 2 «Оптимизация
алгоритмов поиска» ……………...……………….. 18
ПРИЛОЖЕНИЕ А ………………..………...………….. 21
ПРИЛОЖЕНИЕ Б …..…………………………...…….. 26
ПРИЛОЖЕНИЕ В ……………...……………………… 27
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ……...….……... 27
ПРОГРАММА, КОНТРОЛЬНЫЕ ЗАДАНИЯ
И МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по дисциплине «Теория скрытности»
по направлению 11.03.01 «Радиотехника»,
профилю «Радиотехнические средства передачи,
приема и обработки сигналов»
для студентов заочной формы обучения
Составитель: Литвиненко Владимир Петрович
В авторской редакции
ЛР № 066815 от 25.08.99. Подписано к печати 22.12.2015.
Формат 60x84/16. Бумага для множительных аппаратов.
Усл. печ. л. 1,3. Уч.-изд. л. 1,2. Тираж 50 экз. «С»
Зак. №
ГОУВПО «Воронежский государственный технический университет»
394026 Воронеж, Московский просп. 14