Мультипликативные индексные модели.
1.
В статистической практике индексы наряду со средними величинами – наиболее распространенные статистические показатели.
Индексы, как и многие другие статистические показатели, возникли в ответ на требование практики. В начале 18 века широко развиваются рыночные отношения, что поставило вопрос о характеристике динамики цен. Легко рассчитать изменение цены одного товара, определив ее темп роста. Но как определить изменение цен по совокупности товаров?
Цены нельзя непосредственно суммировать, их нужно увязать с количеством продаваемых товаров, то есть взвесить по количеству, как говорят статистики. Однако лишь в 1874 г. Герман Пааше предложил формулу индекса цен, которой пользуются и до сих пор.Учитывая сказанное, дадим определение индексу как статистическому показателю.
Индекс (лат. – показатель) - статистический показатель, который характеризует относительное изменение признака у одной единицы совокупности (индивидуальный индекс) или по совокупности в целом (общий индекс).
Индивидуальный индекс представляет собой темп роста.
Общий индекс, который собственно, является индексом, т.е. особым статистическим показателем, представляет собой относительную величину, которая получилась в результате сопоставления непосредственно не поддающихся суммированию уровней социально-экономических явлений. Сопоставление может вестись во времени, в пространстве и по сравнению с планом.
С точки зрения методики построения общие индексы делятся на агрегатные, средневзвешенные и индексы средних величин.
С точки зрения характеристики индексируемого признака различают индексы объёмных признаков (физический объём производства, потребления и т.д.) и индексы качественных признаков (цена, заработная плата, себестоимость и т.д.).
Обозначения, принятые в теории индексов:
i –индивидуальный индекс
p- цена
q- количество товаров
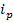 - индекс цены
- индекс цены
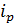 =
= 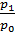
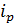 =
= 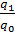
p 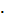 q = p
q = p 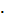 q-стоимость проданного товара
q-стоимость проданного товара
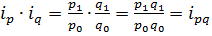 – индекс стоимости
– индекс стоимости
Если признаки связаны между собой мультипликативной связью, то их индексы связаны точно также. (Пример. Фонд заработной платы организации за квартал вырос на 8%, а средняя заработная плата выросла на 10%. Как изменилась численность организации?)
2.
Агрегатный индекс – самая распространённая форма общего индекса. Основной принцип, используемый при построении агрегатного индекса, – принцип взвешивания.
Взвешивание помогает преодолеть невозможность непосредственного суммирования значений признака. Весами являются признаки, экономически связанные с теми признаками, которые индексируются таким образом, чтобы произведение индексируемого признака на вес давало реально существующую экономическую величину. Для цены весом является количество проданного товара, так как произведение цены на количество дает стоимость.
Для количества товара весом является цена, поскольку произведение количества на цену дает стоимость, то есть реальную величину. Для заработной платы – количество рабочих, для урожайности – площадь.
Для того, чтобы изменение весов не исказило изменение индексируемого признака, веса в числителе и знаменателе индекса берутся на уровне одного периода. Для качественных признаков веса в числителе и знаменателе индекса берутся на уровне отчётного периода. Для объёмных признаков веса берутся на уровне предыдущего или базисного периода.
I – общий индекс
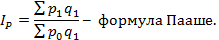
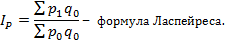
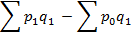
Это – абсолютное изменение стоимости за счет изменения цены.
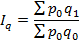
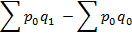
Это - абсолютное изменение стоимости за счет изменения физического объема.
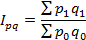
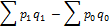
Это - общее абсолютное изменение стоимости.
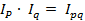
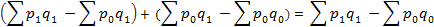
Пример.Имеются следующие данные о динамике продаж и ценах на рынке.
Таблица 11. Динамика продаж и цен товаров на рынке
| Товары | Продано, тыс. тонн | Цена 1 тонны, млн. рублей | ||
| I квартал | II квартал | I квартал | II квартал | |
| А | ||||
| В |
Определить агрегатные индексы цен, объёма продажи и стоимости.
Объяснить их экономический смысл.
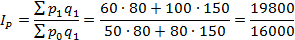
Таким образом, цены на рынке выросли на 23,7%. В результате этого стоимость проданной продукции увеличилась на 19800-16000=3800 млн. рублей.
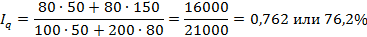
Таким образом, объём продаж снизился на 23,8%. И в результате этого стоимость продаж продукции снизилась на 16000-21000=-5000 млн. рублей.
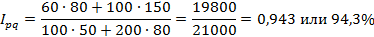
Таким образом, стоимость продукции на рынке снизилась на 5,7% или на 1200 млн. рублей.
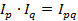
1,237 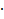 0,762=0,943
0,762=0,943
+3800-5000=-1200
Аналогично записываются индексы и других признаков.
Например:
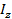 - индекс себестоимости
- индекс себестоимости
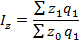
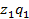 -общие затраты в отчетном периоде.
-общие затраты в отчетном периоде.
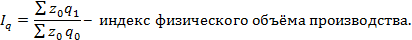
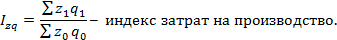
3.
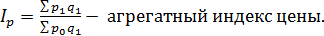
Для того, чтобы рассчитать этот индекс, нужно знать значение индексируемого признака в отчетном и предыдущем периоде. Однако эти значения бывают не всегда известны, а известными бывают относительные изменения признаков. В этом случае для расчёта общих индексов используются средневзвешенные индексы, тождественные агрегатным. Покажем преобразование агрегатных индексов цены.
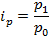
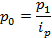
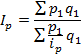
Это – средний гармонический индекс цены, который усредняет индивидуальное изменение цены.
Рассмотрим преобразование агрегатного индекса физического объёма продукции.
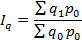
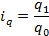
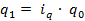
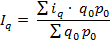
Пример.Имеются следующие данные о динамике цен и объеме продаж на рынке
Таблица 12. Динамика цен и объёма продажи товара на рынке
| Товар | Стоимость товара, млн. руб. | Изменение цены, % | Изменение объёма продаж, % | |
| I квартал | II квартал | |||
| А В | +20 +25 | -20 -25 |
Определить изменение цен, объёмов продаж и стоимости продаж в целом по рынку.
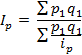
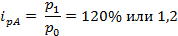
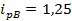
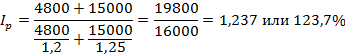
Вывод: Цены в среднем на рынке выросли на 23,7% и в результате этого стоимость проданных товаров выросла на 3800 млн. рублей (см. таблицу 11)
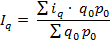
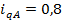
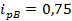
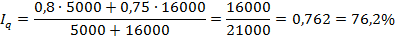
Таким образом, продажи на рынке снизились на 23,8%, и в результате этого стоимость проданной продукции снизится на 5000 млн. рублей.
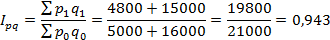
То есть стоимость продаж на рынке снизилась на 5,7% или на 1200 млн. рублей.
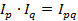
1,237 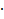 0,762=0,943
0,762=0,943
За счёт роста цены - 3800 3800-5000=-1200
За счёт снижения продаж -5000
Аналогично можно записать средневзвешенные индексы других признаков. Запишем индексы себестоимости, физического объёма производства и затрат на производство.
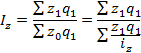
Индекс показывает, как в среднем изменилась себестоимость.
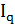 =
= 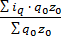
Это - среднеарифметический индекс физического объема производства, который показывает, как в целом изменяется объем производства.
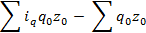
Эта разница показывает абсолютное изменение затрат на производство за счет изменения физического объема производства.
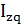 =
= 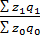
Это – общий индекс затрат.
4.
Одной из важных задач статистики является изучение динамики средних величин. Рассмотрим индексы средних величин на примере индексов средней цены.
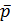 =
= 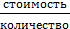 =
= 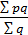 – средняя арифметическая взвешенная =
– средняя арифметическая взвешенная = 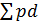
d = 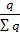 – доля продаж в каждом магазине.
– доля продаж в каждом магазине.
Таким образом, цена товаров зависит от цены товаров в отдельных точках продаж и от структуры продаж, которая характеризуется долями d.
Для того, чтобы определить влияние изменения этих факторов на изменение средней цены, в статистике разработана система индексов, состоящая из следующих индексов:
1. Индекс переменного состава.
2. Индекс постоянного состава.
3. Индекс структурных сдвигов.
1) 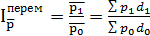 – индекс средней цены переменного состава.
– индекс средней цены переменного состава.
Этот индекс покажет, как изменится средняя цена.
2) 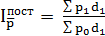 – индекс средней цены постоянного состава.
– индекс средней цены постоянного состава.
Этот индекс покажет, как изменится средняя цена за счет изменения цены в отдельных точках продаж.
3) 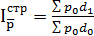 – индекс структурных сдвигов.
– индекс структурных сдвигов.
Покажет, как изменится средняя цена за счет изменения структуры продаж.
Взаимосвязь индексов:
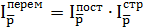
Пример.Имеются следующие данные о динамике цен и продаж товара А на рынках города.
Таблица13. Динамика цен и продаж товара А на рынках города.
| Рынки | Продано, тыс. т. | Цена 1 тонны, тыс. рублей | ||
| I квартал | II квартал | I квартал | II квартал | |
Охарактеризовать изменение средней цены товара А и, в том числе, за счет факторов, на нее влияющих.
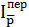 =
= 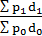 =
= 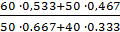 =
= 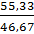 =1,18,5 или 118, 5%.
=1,18,5 или 118, 5%.
Таким образом, средняя цена товара А во II квартале выросла на 8,66 тыс. рублей или на 18,5 %.
Таблица 14. Структура продаж товара А.
| Рынок | I квартал | II квартал |
100 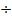 150 = 0,667 50 150 = 0,667 50 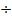 150 = 0,333 150 = 0,333 | 80  150 = 0,533 70 150 = 0,533 70 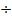 150 = 0,467 150 = 0,467 | |
| Итого | 1,0 | 1,0 |
Во II квартале увеличилась доля 2 рынка. Таким образом, во II квартале выросла доля продаж на втором более дешевым рынке.
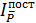 =
= 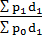 =
= 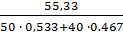 =
= 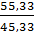 = 1,221, или 122,1 %
= 1,221, или 122,1 %
Таким образом, за счет роста цен на первом и втором рынках средняя цена товара А увеличилась на 10 тыс. рублей или на 22,1%.
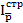 =
= 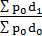 =
= 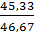 = 0,971 или 97,1 %.
= 0,971 или 97,1 %.
Таким образом, за счет увеличения доли продажи товара А на втором более дешевом рынке, средняя цена товара А снизилась на 1,34 тыс. рублей или на 2,9 %.
Взаимосвязь рассчитанных показателей:
1,221  0,97 = 1,185
0,97 = 1,185
10 - 1,34 = 8,66
Как бы изменилась средняя цена товара А, если бы структура продаж не изменилась? Средняя цена выросла бы на 22,1%.
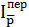 =
= 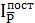 , так как
, так как 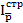 = 1
= 1
Аналогично записываются индексы средних величин для любых качественных признаков.
Запишем индексы средней себестоимости:
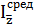 =
= 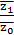 =
= 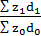 – общее изменение средней себестоимости.
– общее изменение средней себестоимости.
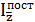 =
= 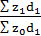 - как изменяется средняя себестоимость за счет изменения себестоимости в отдельных местах производства.
- как изменяется средняя себестоимость за счет изменения себестоимости в отдельных местах производства.
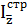 =
= 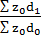 - как изменится средняя себестоимость за счет изменения структуры производства продукции.
- как изменится средняя себестоимость за счет изменения структуры производства продукции.
d – доля производства продукции в отдельной точке производства.
5.
Рассмотрим двухфакторную мультипликативную модель.
R = a 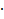 b, где R– результативный признак, a – качественный признак и b– объемный признак.
b, где R– результативный признак, a – качественный признак и b– объемный признак.
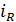 =
= 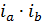
Таким образом, относительное изменение результативного признака под влиянием факторных признаков показывают индивидуальные индексы этих факторных признаков.
Абсолютное изменение результативного признака рассчитывают следующим образом:
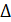 R =
R = 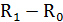 в т.ч.
в т.ч. 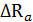 = (
= ( 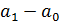 )
) 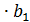 =
= 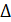 a
a 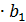 – изменение за счет
– изменение за счет
качественного признака.
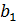 – объем в отчетном периоде
– объем в отчетном периоде
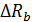 = (
= ( 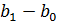 )
) 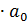 =
= 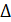 b
b 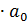 – вес на уровне базисного периода – изменение за счет объемного признака
– вес на уровне базисного периода – изменение за счет объемного признака
Проверка 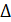 R
R 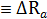 +
+ 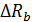
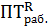
Тема 8. РЯДЫ ДИНАМИКИ
