Тема 3 Группировка статистических данных

Сущность группировки и ее основные виды

Этапы построения группировок

Ряды распределения

Пример построения аналитической группировки

1.

Обработка статистических данных обычно начинается с построения группировок.

Группировка –распределение единиц совокупности на группы однородные в каком-то существенном отношении и характеристика выделенных групп с помощью статистических показателей.

Результаты группировки представляются в виде таблиц.

С помощью группировок решается несколько задач, основными из которых являются:

1) выделение типов социально-экономических явлений – с помощью типологической группировки (например: группировка предприятий по формам собственности, группировка населения по социальным группам и т.д.);

2) изучение структуры статистической совокупности - с помощью структурных группировок и рядов распределения (например: группировка по полу);

3) изучение взаимосвязи между признаками - с помощью аналитической группировки.

Группировка, в которой группы образованы по одному признаку, называется простой. Для характеристики явления бывает недостаточно разбить совокупность на группы по какому-либо одному признаку. В этом случае строят сложные (комбинационные) группировки.

Сложной называется группировка, в которой разделение совокупности на группы производится по двум и более признакам, взятым в сочетании (комбинации).

2.

1)Выбор группировочного признака (признаков) – выбор производится исходя из целей исследования.

2)Определение числа групп и величины интервала группировки.

Если группировка проводится по атрибутивному признаку, то обычно выделяют столько групп, сколько значений этого признака.

Если значений этого признака много, то пользуются классификацией (классификатор профессий).

Если группировка проводится по дискретному признаку и значений этого признака немного, то выделяют столько групп, сколько значений этого признака.

Если группировка проводится по непрерывному признаку или дискретному со многими значениями, то число групп можно определить по следующей формуле:

n = 1+3,322 lgN,

где N-число единиц совокупности.

Если признак непрерывный или дискретный со многими значениями, необходимо найти интервал группировки.

Интервалы бывают:

· равные, когда разность между максимальным и минимальным значениями в каждом из интервалов одинакова;

· неравные, когда, например, ширина интервала постепенно увеличивается, а верхний интервал часто не закрывается вовсе;

· открытые, когда имеется только либо верхняя, либо нижняя граница;

· закрытые, когда имеются и нижняя, и верхняя границы.

В случае равных интервалов величина интервала может быть определена как:

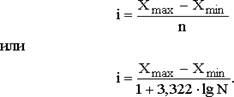
где i - величина интервала;

n – число групп;

Xmax, Xmin – максимальное и минимальное значения признака.

3) Подсчет численности единиц совокупности в каждой группе и по совокупности в целом.

4)Характеристика выделенных групп с помощью различных статистических показателей (Методика их расчета будет рассматриваться в процессе изучения).

5) Оформление результатов группировки в таблице.

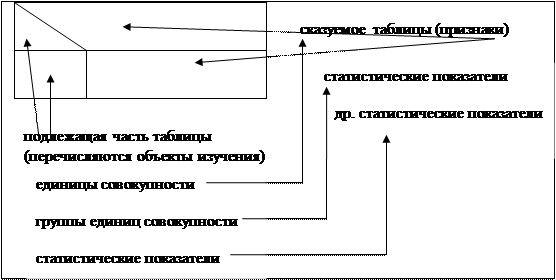
Рис. 2. Схема таблицы

Почти всегда признаки и статистические показатели имеют единицы измерения,которые должны быть указаны в таблице.

После таблицы обязательно должны быть сделаны выводы и разъяснения.

3.

Ряд распределения – это группировка, с помощью которой устанавливается распределение единиц совокупности по величине или значению некоторого признака.

Ряды, построенные по атрибутивному признаку, называются атрибутивными рядами распределения.

Ряды распределения, построенные по количественному признаку, называются вариационными рядами.

Примером атрибутивных рядов могут служить распределения населения по полу, занятости, национальности, профессии и т.д.

Примером вариационного ряда распределения может служить распределение населения по возрасту, рабочих – по стажу работы, заработной плате и т.д.

Вариационные ряды в зависимости от характера вариации подразделяются на дискретные и интервальные.

Вариационные ряды распределения состоят их двух элементов вариантов и частот.

Вариантами называются числовые значения количественного признака в ряду распределения, они могут быть положительными и отрицательными, абсолютными и относительными.

Частоты – это численности отдельных вариантов или каждой группы вариационного ряда. Сумма всех частот называется объемом совокупности и определяет число элементов всей совокупности.

Может быть рассчитана относительная частота, или частость, которая покажет долю каждой группы в совокупности.

Рассмотрим пример дискретного ряда распределения.

Таблица 1. Распределение рабочих цеха по

Тарифным разрядам

Тарифный разряд	Число рабочих	В % к итогу	Накопленная частота
		20,0 32,0 30,0 11,0 7,0
итого		100,0	----

1) Тарифный разряд – признак, по которому распределяют. 2,3,4,5,6 – варианты.

2) Число рабочих: 40, 64, 60, 22, 14 – частоты.

3) В % к итогу: 20,0; 32,0; 30,0; 11,0; 7,0 – частости.

Выводы: в этом цехе больше половины рабочих имеют 3 и 4 разряды, т.е. средний уровень квалификации.

Графически дискретный ряд распределения может быть представлен полигоном распределения.

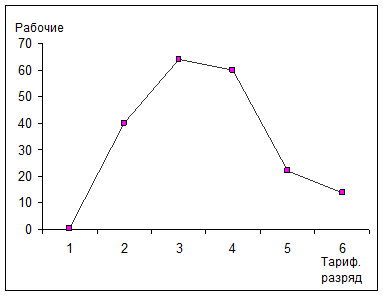
Рис. 3. Распределение рабочих цеха по тарифным разрядам

Пример. По следующим данным построить интервальный ряд распределения, выделив 4 группы предприятий с равными интервалами по величине основных средств.

Таблица 2. Стоимость основных средств и объем продукции

По предприятиям

Номер предприятия	Основные средства, млрд. руб	Объем продукции, млрд. руб.
	1,8 1,2 2,8 2,4 3,1 5,2 3,9 3,5 3,5 4,3 4,5 4,0	2,2 1,0 2,8 2,9 3,6 6,4 4,3 4,6 4,5 5,6 5,4 4,8

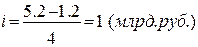
Таблица 3. Распределение предприятий