Основные законы массопередачи.

В процессах переноса распределяемого вещества (массы) из одной фазы в другую надлежит различать два случая:

1) перенос из потока жидкости в поток жидкости, или сассообмен между потоками жидкости

2) перенос из твёрдого тела в поток жидкости (или перенос в обратном направлении), то есть массообмен между твёрдой фазой, содержащей внутри пор или капилляров распределяемое вещество, и потоком жидкости.

Элементарными законами, которым подчиняется перенос распределяемого вещества из одной фазы в другую, является закон молекулярной диффузии, закон массоотдачи и закон массопроводности.

Закон молекулярной диффузии (первый закон Фика)

Количество продиффундировавшего вещества пропорционально градиенту концентраций, площади, перпендикулярной направлению диффузионного потока, и времени:

,

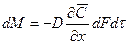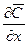где - количество продиффундировавшегося вещества, - градиент концентрации в направлении диффузии; - элементарная площадка, черз которую происходит диффузия; 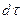- время диффузии; 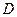- коэффициент пропорциональности, или коэффициент диффузии.

Коэффициент диффузии показывает, какое количество вещества диффундирует через поверхность в 1 м² в течение 1 ч при разности концентраций на расстоянии 1 м, равной единице.

Знак минус в правой части уравнения показывает, что при молекулярной диффузии в направлении перемещения вещества концентрация убывает.

Коэффициент диффузии не является постоянной величиной; численные значения его обычно берут из справочников или находят по следующим формулам:

Для газов:

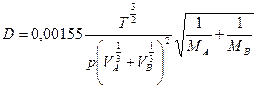
Для жидкостей:

,

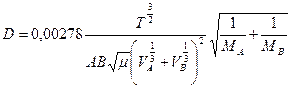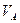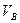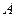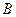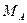где - абсолютная температура в °К; - давление в атм; и - мольные объёмы взаимодействующих веществ и ; и 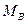- молекулярные веса взаимодействующих веществ; 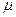- вязкость жидкости, в которой происходит диффузия, в спз; 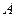и 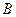- опытные константы, зависящие от природы вещества.

Коэффициент диффузии зависит, прежде всего, от агрегатного состояния систем: так, коэффициент диффузии для газов примерно на четыре порядка выше, чем для жидкостей. Коэффициент диффузии увеличивается с ростом температуры и уменьшается с повышением давления.

Для концентрированных растворов:

,

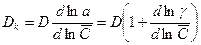где 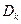- коэффициент диффузии в растворе с концентрацией 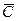; 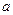- активность диффундирующего вещества; 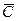- концентрация диффундирующего вещества; 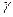- коэффициент активности.

Дифференциальное уравнение молекулярной диффузии (второй закон Фика)

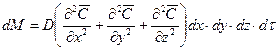(11.44)

С другой стороны, ту же прибыль качества диффундирующего вещества в элементе параллелепипеда можно найти умножением объёма элемента на изменение концентрации за время 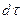, то есть:

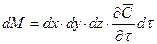(11.45)

Сопоставляя соотношения 11.44 и 11.45, получим дифференциальное уравнение молекулярной диффузии:

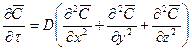(11.46)

Закон массоотдачи (закон Щукарёва)

Закон Щукарёва может быть сформулировать так: количество вещества, перенесённого от поверхности раздела фаз в воспринимающую фазу, пропорционально разности концентраций у поверхности раздела фаз и в ядре потока воспринимающей фазы, поверхности фазового контакта и времени.

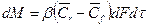(11.47)

где 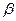- коэффициент массоотдачи, характеризующий перенос вещества конвективными и диффузионными потоками одновременно; 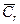- концентрация в воспринимающей фазе у поверхности раздела фаз; 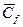- концентрация в ядре потока воспринимающей фазы; остальные обозначения прежние. При этом важно отметить, что концентрация на границе 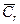рассматривается как равновесная концентрация.

Коэффициент массоотдачи показывает, какое количество вещества передаётся от поверхности раздела фаз в воспринимающую фазу через 1 м² поверхности фазового контакта в течение 1 ч при разности концентраций 1 кг/м³.

Дифференциальное уравнение массоотдачи.

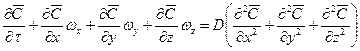(11.51)

Критериальное уравнение конвективной диффузии. Выведенное дифференциальное уравнение (11.51) является математическим описанием процесса перемещения вещества в жидкой (газовой, паровой) фазе конвективной диффузией. Для полнго математического описания процесса это уравнение должно быть дополнено уравнением, характеризующим условия на границе рассматриваемой фазы. Количества вещества, перемещающегося из фазы в фазу у границы, можно определить исходя из основного закона конвективной диффузии: 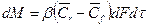, или, обозначая 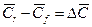, получим:

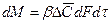(11.52)

Это же количество вещества может быть определено другим способом. У поверхности раздела фаз вещество переходит в другую фазу за счёт молекулярной диффузии. На этом участке пути количество переданного из фазы в фазу вещества можно найти исходя из основного закона молекулярной диффузии:

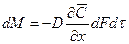
Очевидно, что величина в последнем уравнении и в уравнении (11.52) представляет собой одно и то же количество вещества, выраженное различными способами, и, следовательно:

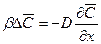(11.53)

Уравнения (11.51) и (11.53) не разрешимы для встречающихся в практике случаев и, следовательно, не могут служить для непосредственного определения численных значений коэффициентов массоотдачи. Поэтому в расчётной практике пользуются критериальными уравнениями, полученными из уравнений (11.52) и (11.53).

Для получения диффузионных критериев подобия преобразуем уравнения (11.51) и (11.53) методами теории подобия. Из уравнения (11.53) делением обеих частей уравнения на правую часть получим безразмерный комплекс:

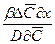
Вычеркнув в полученном комплексе символы дифференцирования, разности и направления (замена х на не ориентированный в определённом направлении линейный размер 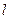), после сокращения получаем диффузионный критерий Нуссельта:

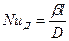(11.54)

Из дифференциального уравнения конвективной диффузии:

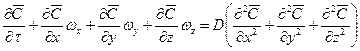
получаем безразмерные комплексы делением всех членов уравнения на :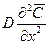

;

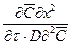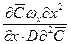
Вычеркнув в полученных комплексах символы дифференцирования (включая символы порядка дифференцирования) и направления, после сокращений получаем диффузионный критерий Фурье:

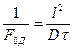или 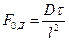(11.55)

И диффузионный критерий Пекле:

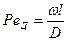(11.56)

Критерий 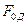характеризует изменение скорости потока диффундирующей массы во времени; он необходим только для характеристики нестационарных процессов диффузии.

Критерий 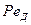обычно преобразовывают и представляют его в виде произведения двух критериев:

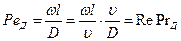
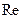является критерием гидродинамического подобия, а новый критерий 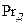- диффузионный критерий Прандтля – находится лишь по физическим параметрам и характеризует подобие полей физических величин:

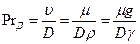(11.57)

В случаях, когда массообмен протекает в условиях естественной конвекции, вызванной разностью плотностей растворов с различной концентрацией, для характеристики процесса вместо критерия 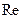(или дополнительно к нему) вводят критерий Грасгофа.

Полученный критерий подобия даёт возможность найти Критериальное уравнение конвективной диффузии:

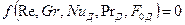(11.58)

Из всех критериев уравнения (11.58) только 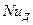не состоит целиком из условий однозначности, поэтому он является определяемым критерием. Исходя из этого уравнение (11.58) представляется в виде:

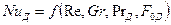(11.59)

Применительно к конкретным задачам массообмена общее критериальное уравнение (11.59) может быть упрощено. При рассмотрении стационарных процессов массообмена из критериального уравнения выпадает критерий 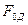, и оно имеет вид:

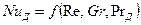(11.60)

При вынужденном движении потока фазы естественной конвекции можно пренебречь, тогда из уравнения выпадает критерий :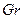

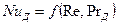(11.61)

или

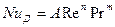(11.62)

В условиях естественной конвекции фазы из уравнения выпадает критерий :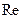

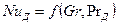(11.63)

или

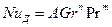(11.64)

По найденным из критериальных уравнений значениям 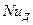легко определяют коэффициенты массоотдачи:

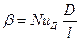(11.65),

а по ним и коэффициенты массопередачи.

Выражение коэффициента массопередачи через коэффициенты массоотдачи.

Определение коэффициента массопередачи :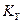

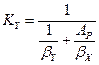(11.67)

Определение коэффициента массопередачи :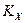

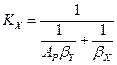(11.68)

.

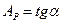Коэффициент массоотдачи представляет собой величину, которая учитывает сопротивление переносу вещества за счёт молекулярной диффузии, а также сопротивление переносу потоками жидкости, то есть чисто конвективному переносу. Следовательно, на величину коэффициентов массоотдачи оказывают влияние все те факторы, которые определяют скорость молекулярной диффузии, а также скорость конвективного переноса.