Занятие № 1. Случайные события. Алгебра событий.

Задания.

1. Построить множество элементарных исходов Ω по описанию эксперимента и подмножества, соответствующие указанным событиям. Выявить пары совместных событий.

а) Игральная кость подбрасывается дважды. Наблюдаемый результат – пара чисел, соответствующих числам очков, выпавших в первый и второй раз. События: А – оба раза выпало число очков, кратное трем; В – ни разу не выпало число шесть; С – оба раза выпало число очков, больше трех; D – оба раза выпало одинаковое число очков.

б) Монета подбрасывается три раза. Наблюдаемый результат – появление герба (г) или цифры (ц) на верхней стороне монеты. События А – герб выпал ровно один раз; В – ни разу не выпала цифра; С – выпало больше гербов, чем цифр.

в) Монета подбрасывается до первого появления герба. Наблюдаемый результат – общее число подбрасываний. События: А – герб выпал при третьем подбрасывании, В – герб выпал не ранее, чем при третьем подбрасывании.

е) Иван и Петр договорились о встрече в определенном месте между одиннадцатью и двенадцатью часами. Каждый приходит в случайный момент указанного промежутка и ждет появления другого до истечения часа, но не более 15 минут, после чего уходит. Наблюдаемый результат – пара чисел (х;у), где х – время прихода Петра, у – время прихода Ивана (время исчисляется в минутах, начиная от 11 часов). События А – встреча состоялась, В – Петр ждал Ивана все обусловленное время и не дождался, С – Ивану не пришлось ждать Петра.

2. Являются ли несовместными следующие события: а) опыт – бросание монеты; события: А₁ – появление герба, А₂ – появление цифры; б) опыт – бросание двух монет; события: В₁ – появление двух гербов, В₂ – появление двух цифр; в) опыт – два выстрела по мишени; события: А₀ – ни одного попадания; А₁ – одно попадание; А₂ – два попадания; г) опыт – два выстрела по мишени; события: С₁ – хотя бы одно попадание; С₂ – хотя бы один промах.

3. Образуют ли полную группу следующие события: а) опыт – бросание монеты; события: А₁ – появление герба, А₂ – появление цифры; б) опыт – бросание двух монет; события: В₁ – появление двух гербов, В₂ – появление двух цифр; в) опыт – два выстрела по мишени; события: А₀ – ни одного попадания; А₁ – одно попадание; А₂ – два попадания; г) опыт – два выстрела по мишени; события: С₁ – хотя бы одно попадание; С₂ – хотя бы один промах.

4. Игральная кость подбрасывается один раз. Обозначим х число очков, выпавших на верхней грани. События A={х кратно трем}, B={х нечетно}, C={х>3}, D={х<7}, E={х дробно}, F={0,5<x<1,5}. Описать состав и выяснить смысл следующих событий: Е₁= 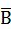, Е₂= 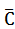, Е₃=АВ, Е₄=А+В, Е₅=А- 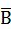, Е₆=Е+D, Е₇ = EF.

5. В урне 5 красных, 2 синих и 3 белых шара. Все они пронумерованы цифрами от 1 до 10. Из урны берется один шар. События – шар с четным номером – обозначим через А, с номером, кратным 3, - через В, шар красного цвета – через С, синего – через – D, белого – через Е. Что представляют собой следующие события: А+В, С+Е, АD, А-В, ВЕ, АD-Е?

6. По мишени производится три выстрела. Рассмотрим события – А_i попадание при i-м выстреле (i=1,2,3). Представить в виде сумм, произведений или сумм произведений событий А_i и Ā_i следующие события: А – все три попадания, В – все три промаха, С – хотя бы одно попадание, D – хотя бы один промах, Е – не менее двух попаданий.

7. Произведено три выстрела из орудия по цели. Событие
A_k = {попадание при к-м выстреле} (к = 1, 2, 3).

а) Выяснить состав множества Ω, выразив каждый элементарный исход ω_i через события A_k.

б) Записать в алгебре событий следующие события:

А — {ровно одно попадание}, В = {хотя бы одно попадание}, С = {хотя бы один промах}, D — {не меньше двух попаданий}, Е={попадание не раньше, чем при третьем выстреле}.

8. Два баскетболиста по очереди бросают мяч в корзину до
первого попадания. Выигрывает тот, кто первый забросит мяч.
События: A_k={первый баскетболист попадает при своем к-м
броске}, В_k={второй баскетболист попадает при своем к-м броске};
А={выигрывает первый баскетболист}, В={выигрывает второй}. Первый баскетболист бросает первым. Определить состав множества элементарных исходов и записать события А и В в алгебре событий.