Иррациональные уравнения. Уравнения и неравенства с модулем
Цель: Знать правила избавления от иррациональности, раскрытия модуля числа и уметь пользоваться ими при решении уравнений и неравенств.
Методические рекомендации
Формулы для повторения:
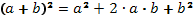 ;
;
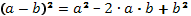 ;
;
Решение квадратных уравнений:
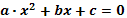
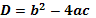 ,
,
Если 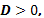 то
то 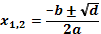
Если 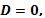 то
то 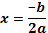
Если 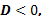 то корней нет
то корней нет
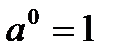 ;
; 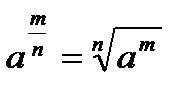 ;
; 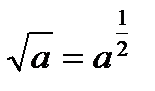 ;
; 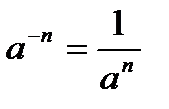 ;
; 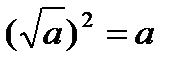 ;
; 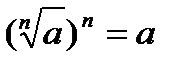
1. Изучив тему, письменно ответьте на вопросы:
10. Введите понятие иррационального уравнения.
20. Сформулируйте утверждение и замечание на с.350.
30. Решение уравнений, содержащих квадратные радикалы.
40. Записать решение примера 60, с. 351.
50. Метод уединения радикалов (прим. 61).
60. Сформулируйте утверждение на с. 352.
70. Дайте определение 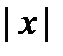 и его иной формы.
и его иной формы.
80. Таблица решения элементарных уравнений и неравенств с модулем.
90. Записать решение примера 85, с. 74.
100. Запишите вывод о решении неравенства с модулем.
110. Запишите решение примера 90, с. 76.
2. Выполните письменно задания:
| 1 вариант | 2 вариант |
1. Решите уравнения: а) 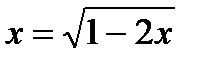 ; б) ; б) 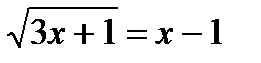 ; в) ; в) 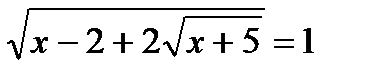 . . | 1. Решите уравнения: а) 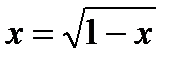 ; б) ; б) 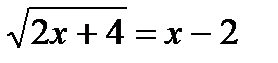 ; в) ; в) 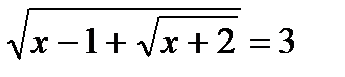 . . |
2. Решите уравнения: а) 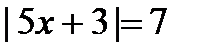 ; б) ; б) 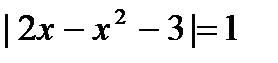 . . | 2. Решите уравнения: а) 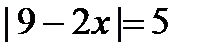 ; б) ; б) 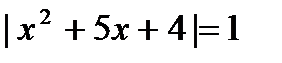 . . |
3. Решите неравенства: а) 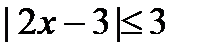 ; б) ; б) 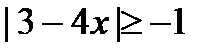 . . | 3. Решите неравенства: а) 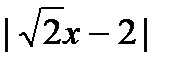 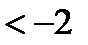 ; б) ; б) 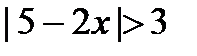 . . |
Литература: М.Я. Пратусевич «Алгебра и начала анализа», 10кл., М., «Просвещение» 2014, гл. I, §10; 11кл.-гл.XIII, §84.
Самостоятельная работа № 36.
Графическое решение уравнений и неравенств
Цель: Уметь с помощью графика находить решение уравнений и неравенств.
Изучив тему, письменно ответьте на вопросы:
1. Графическая интерпретация решения уравнения 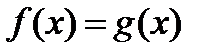 .
.
2. Графическая интерпретация решения неравенства 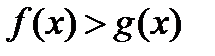 .
.
3. Определение числа корней уравнения 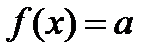 (графическое).
(графическое).
4. Записать решение прим.18, с. 193.
Литература: М.Я. Пратусевич «Алгебра и начала математического анализа» 10кл., М., «Просвещение», 2014, с.193.
Самостоятельная работа № 37.
Разные подходы к решению систем уравнений и неравенств
Цель: Уметь различными способами находить решение уравнений и неравенств.
Изучив тему, решить задания:
1) Решите неравенства методом интервалов:
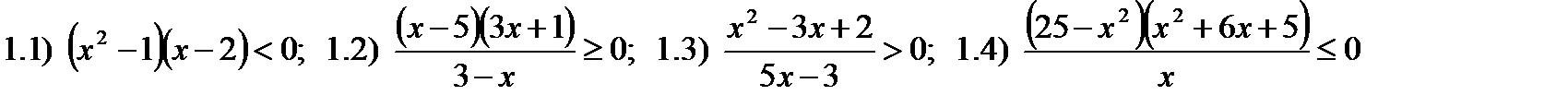
2) Решите задачи:
2.1) Для одного из предприятий-монополистов зависимость объема спроса на продукцию q (единиц в месяц) от ее цены p (тыс. руб.) задается формулой: 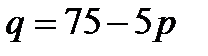 . Определите максимальный уровень цены (в тыс. руб.), при котором значение выручки предприятия за месяц
. Определите максимальный уровень цены (в тыс. руб.), при котором значение выручки предприятия за месяц 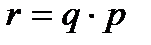 составит не менее 270 тыс. руб.
составит не менее 270 тыс. руб.
2.2) Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур задается выражением: 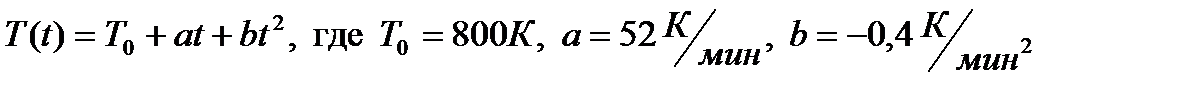 . Известно, что при температуре нагревателя свыше 2000 К прибор может испортиться, поэтому его нужно отключать. Определите (в минутах), через какое наибольшее время после начала работы нужно отключить прибор.
. Известно, что при температуре нагревателя свыше 2000 К прибор может испортиться, поэтому его нужно отключать. Определите (в минутах), через какое наибольшее время после начала работы нужно отключить прибор.
Итоговая самостоятельная работа
Подготовка к экзамену
Цель: проверка знаний студентов.
1 вариант
1. Отрезок 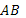 имеет с плоскостью
имеет с плоскостью 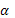 единственную общую точку А. Точка С делит его в отношении 3:1, считая от точки А. Через точки С и В проведены параллельные прямые, пресекающие плоскость
единственную общую точку А. Точка С делит его в отношении 3:1, считая от точки А. Через точки С и В проведены параллельные прямые, пресекающие плоскость 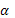 соответственно в точках С1 и В1. Длина отрезка АС1 равна 16 см. Найдите длину отрезка АВ1.
соответственно в точках С1 и В1. Длина отрезка АС1 равна 16 см. Найдите длину отрезка АВ1.
2. Ромб со стороной 12 см и острым углом 600 вращается около стороны. Найдите объем тела вращения.
3. Решить уравнение: 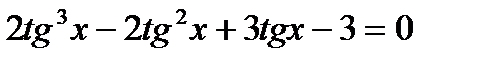
4. Решить систему уравнений: 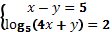
5. Найдите угловой коэффициент касательной, проведенной к графику функции 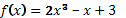 в точке с абсциссой
в точке с абсциссой 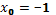 .
.
6. Решить уравнение: 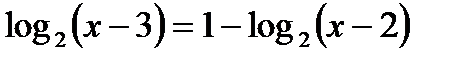
7. Решите уравнение: 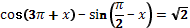
8. Найдите все первообразные функции: 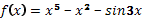
9. Радиус основания цилиндра равен 4 см, площадь боковой поверхности вдвое больше площади основания. Найти объем цилиндра.
10. Найдите область определения: 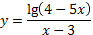 .
.
2 вариант
1. Отрезок 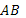 имеет с плоскостью
имеет с плоскостью 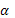 единственную общую точку А. Точка С делит его в отношении 3:2, считая от точки А. Через точки С и В проведены параллельные прямые, пресекающие плоскость
единственную общую точку А. Точка С делит его в отношении 3:2, считая от точки А. Через точки С и В проведены параллельные прямые, пресекающие плоскость 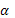 соответственно в точках С1 и В1. Длина отрезка АС1 равна 15 см. Найдите длину отрезка АВ1.
соответственно в точках С1 и В1. Длина отрезка АС1 равна 15 см. Найдите длину отрезка АВ1.
2. Ромб со стороной 18 см и острым углом 600 вращается около стороны. Найдите объем тела вращения.
3. Решить уравнение: 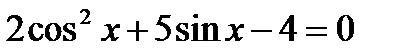
4. Решить систему уравнений: 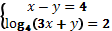
5. Найдите угловой коэффициент касательной, проведенной к графику функции 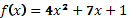 в точке с абсциссой
в точке с абсциссой 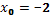 .
.
6. Решить уравнение: 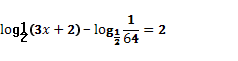
7. Решите уравнение: 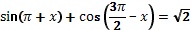
8. Найдите все первообразные функции: 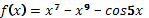
9. Радиус основания цилиндра равен 3 см, площадь боковой поверхности втрое больше площади основания. Найти объем цилиндра.
10. Найдите область определения: 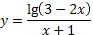 .
.
3 вариант
1. Отрезок 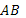 имеет с плоскостью
имеет с плоскостью 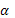 единственную общую точку А. Точка С делит его в отношении 2:3, считая от точки А. Через точки С и В проведены параллельные прямые, пресекающие плоскость
единственную общую точку А. Точка С делит его в отношении 2:3, считая от точки А. Через точки С и В проведены параллельные прямые, пресекающие плоскость 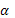 соответственно в точках С1 и В1. Длина отрезка АС1 равна 20 см. Найдите длину отрезка АВ1.
соответственно в точках С1 и В1. Длина отрезка АС1 равна 20 см. Найдите длину отрезка АВ1.
2. Ромб со стороной 24 см и острым углом 600 вращается около стороны. Найдите объем тела вращения.
3. Решить уравнение: 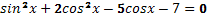
4. Решить систему уравнений: 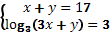
5. Найдите угловой коэффициент касательной. Проведенной к графику функции 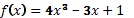 в точке с абсциссой
в точке с абсциссой 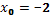 .
.
6. Решить уравнение: 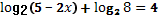
7. Решите уравнение: 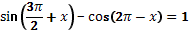
8. Найдите все первообразные функции: 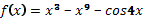
9. Радиус основания цилиндра равен 6 см, площадь боковой поверхности в четыре раза больше площади основания. Найти объем цилиндра.
10. Найдите область определения: 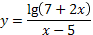 .
.
ЛИТЕРАТУРА
1. Александров А.Д. Математика : алгебра и начала математического анализа, геометрия. Геометрия. 10 класс : учеб. для общеобразоват. организаций: углубл. уровень / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. – М. : Просвещение, 2014. – 271 с.
2. Александров А.Д. Математика : алгебра и начала математического анализа, геометрия. Геометрия 11 класс : учеб. для общеобразоват. организаций: углубл. уровень / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. – М. : Просвещение, 2014. – 272 с.
3. Башмаков М.И. Математика. Задачник : учеб. пособие для студ. учреждений сред. проф. образования / М.И. Башмаков. – 4-е изд., стер. – М. : Издательский центр «Академия» , 2014. – 416 с.
4. Башмаков М.И. Математика : учебник для студ. учреждений сред. проф. образования / М.И. Башмаков. – 9-е изд., стер. – М. : Издательский центр «Академия», 2014. – 256 с.
5. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс : учеб. для общеобразоват. организаций : базовый и углубл. уровни / [С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]. – М. : Просвещение, 2014. – 431 с.
6. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс : учеб. для общеобразоват. организаций : базовый и углубл. уровни / [С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]. – М. : Просвещение, 2014. – 464 с.
7. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни / [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – М. : просвещение, 2014. – 255 с.
8. Пратусевич М.Я. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс : учеб. для общеобразоват. организаций: углубл. уровень / М.Я. Пратусевич, К.М. Столбов, А.Н. Головин. – М. : Просвещение, 2014. – 415 с.
9. Пратусевич М.Я. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс : учеб. для общеобразоват. организаций: углубл. уровень / М.Я. Пратусевич, К.М. Столбов, А.Н. Головин. – М. : Просвещение, 2014. – 463 с.
